模数转换器 (ADC)
最新课程
- MSPM0G 系列 MCU 时钟配置:在 LED 闪烁的情况下动手操作
- Code Composer Studio™ v20 入门
- 双 DMA 正弦波环回:在 MSPM0G 上实现从 DAC 生成到 ADC 捕捉
- MSPM0G3507 动态 CRC 配置和实时验证
- 视频系列:tiarmclang 编译器
- 汽车应用中的 Jacinto™ 7 处理器
- 可以在 2 分钟内实现无线基础设施应用
- TI 超声成像系统电源方案介绍
- TI 连续血糖监测(CGM)方案介绍
- AI 智能眼镜充电的需求与续航力
热门课程
5.1 频域介绍
欢迎参加 TI 高精密实验室
本章节将讨论 ADC 的频域特性
包含频域指标简介
比如 SNR 和 THD
时域和频域是描述信号的两个维度
时域显示的是幅度随着时间的变化
而频域显示的是幅度随着频率的变化
左图是一个1V、1kHz的信号
和0.1V 10kHz 的信号叠加在时域中的体现
对这个波形做傅立叶变换
可以得到频域信号
频域显示仅仅在这两个频点上有幅度
没有时间细节
所以仅仅显示 1k 和 10k 信号的幅度
这个周期信号的频域表现
下面分析一下非周期信号的频域表现
任何波形可以分解为无穷的正弦信号叠加
这个无穷的序列叫傅立叶级数
左图显示了三角波的傅立叶级数
每一项代表正弦信号频率的幅度和相位
级数的第一项叫基频
后面的项数叫谐波
理想的三角波需要无穷的正弦波来构成
然后基波加上几次谐波
也可以得到一个较好的三角波
左图使用了基波和四次谐波来构建三角波
从时域上来看
三角波已经很接近了
对这个三角波做傅里叶变换
可以得到这个三角波的频域表现
为基波加四次谐波,和之前一致
ADC 的传递函数和量化噪声
后续会对这个噪声进行频域分析
左图是一个 4Bit 的 ADC 传递函数
横坐标为模拟电压输出
纵坐标为相应的数字输出
每一个数字对应一个模拟输入
而好多个模拟输入对应同一个数字输出
这里就产生一个小于 1LSB 的模拟误差
这个误差叫量化误差
这个误差叫量化误差
右图显示输入正弦波的输出数字情况
在图片的地方可以看到
数字和模拟之间的区别
这就是正弦信号的量化误差
量化误差可以等效为噪声
称为量化噪声
可以通过量化误差积分
得到量化噪声的有效值
下面看一下量化造成的频域表现
左图为数字傅立叶变换的结果
信号为 1kHz
量化误差产生的量化噪声
也同时显示在波形里面
如果 ADC 为理想 ADC
仅仅考虑量化噪声
可以通过对量化噪声的时域积分得到
然而实际 ADC 还有其他的噪声源
然而实际 ADC 还有其他的噪声源
可以通过本底噪声谱来计算 ADC 的 SNR
下面讨论一下
SNR 就是信噪比的计算
简单来说
信噪比就是描述信号有多纯净的参数
高 SNR 意味着信号比噪声大很多
低信噪比意味着噪声相对是比较大的
信噪比的计算使用信号的有效值
除以噪声的有效值
取对数乘以20得到
ADC的理想信噪比公式为
6.02 乘以 ADC 的位数加上1.76
例如 10Bit ADC 能达到理想信噪比为 61.96dB
理想信噪比仅仅考虑了量化噪声
这是最理想的情况
实际的 ADC 还会有一些其他的噪声源
信噪比会低于计算得到的值
这个表给出了不同分辨率下ADC的理想信噪比
SNR的公式就是
6.02 乘以 ADC 的位数加上1.76
例如一个 16Bit ADC 理想信噪比为 98.08dB
实际的 ADC 可以无限接近这个值
前面讨论了ADC的 SNR
下面讨论ADC的总谐波失真
总谐波失真是 ADC 的一个重要 AC 指标
主要来源于非线性
非线性表征实际的传递函数
与理想的直线传递函数之间的差异
左图分别描述了理想线性传递函数
和实际非线性情况的差别
理想情况下可以描述为 Y=mx+B
非线性需要更多的高次项来描述
右图的例子
可以帮助理解这种非线性
在幅度较低的时候
输出和输入跟随较好
到了高幅度的区域
输出将输入扩展
表现在正弦波上
就是后半个周期扩展了
这种扩展会产生较大的失真
将非线性失真波形做频谱分析
发现信号中有非常多的谐波
这些谐波来源于上半个周期的非线性
谐波是基波的整数倍
如果输入信号是 1kHz
那么输出信号是 2、3、4等谐波
有时候将奇次谐波和偶次谐波分开考虑
因为两者产生的机理不一样
2k 和 4k 就是偶次谐波
1k 和 3k 就是奇次谐波
如果输出的量化数字信号完美的跟随输入
将不会产生谐波
THD 也是一种用分贝表示比例
IEEE 国际标准要求 ADC 测试十次谐波
用于计算THD
取谐波电压的均方根值
除以信号的均方根值
取对数乘以20得到分贝值
THD+N 需要将总噪声添加到计算公式
SINAD 是 SNR 的失真的简称
SINAD 和 THD+N
总是会比单独的 THD
或者 SNR 要差一些
因为同时考虑了噪声和非线性两种误差
注意到用于计算 THD 的谐波分量
而在计算 SNR 的时候除掉了
计算 SNR 的时候
将谐波替换为平坦的底噪来计算
因为谐波和噪声是两种不同的误差来源
需要单独计算
好的
本章节就到这里
你也可以通过测验题来提高面对这个章节的理解
谢谢
-
 未学习 1.1 数据转换器介绍 - 直流参数
未学习 1.1 数据转换器介绍 - 直流参数
-
 未学习 1.2 数据转换器介绍 - 交流和直流参数
未学习 1.2 数据转换器介绍 - 交流和直流参数
-
 未学习 2.1 数据转换器介绍 - SAR型ADC输入类型
未学习 2.1 数据转换器介绍 - SAR型ADC输入类型
-
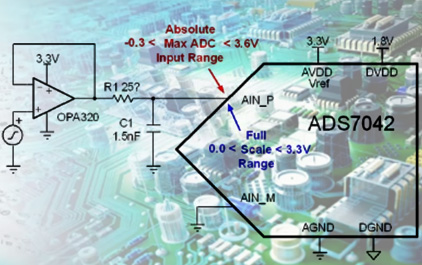 未学习 2.2.1 单端驱动电路分析
未学习 2.2.1 单端驱动电路分析
-
 未学习 2.2.2 反向配置与轨对轨放大器的交越失真
未学习 2.2.2 反向配置与轨对轨放大器的交越失真
-
 未学习 2.3.1 交越失真实验所需硬件软件
未学习 2.3.1 交越失真实验所需硬件软件
-
 未学习 2.3.2 交越失真实验软件设置
未学习 2.3.2 交越失真实验软件设置
-
 未学习 2.3.3 交越失真实验结果
未学习 2.3.3 交越失真实验结果
-
 未学习 2.4.1 仪表放大器输入范围计算
未学习 2.4.1 仪表放大器输入范围计算
-
 未学习 2.4.2 使用软件验证仪表放大器输入共模范围
未学习 2.4.2 使用软件验证仪表放大器输入共模范围
-
 未学习 2.5.1 全差分放大器及失真
未学习 2.5.1 全差分放大器及失真
-
 未学习 2.5.2 全差分驱动电路设计
未学习 2.5.2 全差分驱动电路设计
-
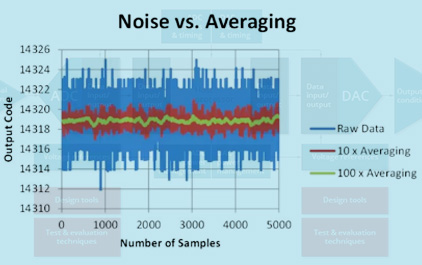 未学习 3.1 误差分析背后的统计学知识
未学习 3.1 误差分析背后的统计学知识
-
 未学习 3.2 理解与校准ADC系统的偏移和增益误差
未学习 3.2 理解与校准ADC系统的偏移和增益误差
-
 未学习 3.3 使用蒙特卡罗SPICE工具进行误差统计分析
未学习 3.3 使用蒙特卡罗SPICE工具进行误差统计分析
-
 未学习 4.1 计算ADC系统的总噪声
未学习 4.1 计算ADC系统的总噪声
-
 未学习 4.2 动手实验-ADC噪声
未学习 4.2 动手实验-ADC噪声
-
 未学习 4.3 ADC 系统中的噪声
未学习 4.3 ADC 系统中的噪声
-
 未学习 4.4 ADC 噪声测量、方法和参数
未学习 4.4 ADC 噪声测量、方法和参数
-
 未学习 4.5 低速 Δ-Σ ADC 的系统噪声性能
未学习 4.5 低速 Δ-Σ ADC 的系统噪声性能
-
 未学习 4.6 分析和计算 ADC 系统中的噪声带宽——多级滤波器
未学习 4.6 分析和计算 ADC 系统中的噪声带宽——多级滤波器
-
 未学习 4.7 分析和计算 ADC 系统中的噪声带宽——数字滤波器
未学习 4.7 分析和计算 ADC 系统中的噪声带宽——数字滤波器
-
 未学习 4.8 增益对噪声、ADC FSR 和动态范围的影响
未学习 4.8 增益对噪声、ADC FSR 和动态范围的影响
-
 未学习 4.9 计算放大器 + ADC 总噪声:设计示例
未学习 4.9 计算放大器 + ADC 总噪声:设计示例
-
 未学习 4.10 ADC 系统中的参考噪声简介
未学习 4.10 ADC 系统中的参考噪声简介
-
 未学习 4.11 参考噪声对信号链性能的影响
未学习 4.11 参考噪声对信号链性能的影响
-
 未学习 4.12 降低参考噪声
未学习 4.12 降低参考噪声
-
 未学习 5.1 频域介绍
未学习 5.1 频域介绍
-
 未学习 5.2 快速傅立叶变换及加窗函数
未学习 5.2 快速傅立叶变换及加窗函数
-
 未学习 5.3 改善频率指标的方法:相干采样及滤波
未学习 5.3 改善频率指标的方法:相干采样及滤波
-
 未学习 5.4 混叠及抗混叠滤波器
未学习 5.4 混叠及抗混叠滤波器
-
 未学习 5.5 实验 - 混叠和抗混叠滤波器
未学习 5.5 实验 - 混叠和抗混叠滤波器
-
 未学习 6.1 SAR ADC及其器件选型
未学习 6.1 SAR ADC及其器件选型
-
 未学习 6.2 驱动放大器的选型和验证
未学习 6.2 驱动放大器的选型和验证
-
 未学习 6.3 建立SAR ADC的仿真模型
未学习 6.3 建立SAR ADC的仿真模型
-
 未学习 6.4 如何计算RC滤波器的值
未学习 6.4 如何计算RC滤波器的值
-
 未学习 6.5 最终的仿真验证
未学习 6.5 最终的仿真验证
-
 未学习 6.6 滤波器RC选型的理论计算方法
未学习 6.6 滤波器RC选型的理论计算方法
-
 未学习 6.7 R-C组件选择背后的数学
未学习 6.7 R-C组件选择背后的数学
-
 未学习 7.1 电压基准概述
未学习 7.1 电压基准概述
-
 未学习 7.2 参考驱动器拓扑概述
未学习 7.2 参考驱动器拓扑概述
-
 未学习 7.3 了解SAR参考输入模型
未学习 7.3 了解SAR参考输入模型
-
 未学习 7.4 开发SAR输入参考模型
未学习 7.4 开发SAR输入参考模型
-
 未学习 7.5 驱动参考实验
未学习 7.5 驱动参考实验
-
 未学习 7.6 ADC:SAR 基准输入 - CDAC
未学习 7.6 ADC:SAR 基准输入 - CDAC
-
 未学习 8.1 SAR ADC功率调节
未学习 8.1 SAR ADC功率调节
-
 未学习 8.2 动手实验 - 系统功率调节
未学习 8.2 动手实验 - 系统功率调节
-
 未学习 9.1 EOS和ESD
未学习 9.1 EOS和ESD
-
 未学习 9.3 向TINA 导入二极管PSpice模型
未学习 9.3 向TINA 导入二极管PSpice模型
-
 未学习 9.4 通过高压放大器保护低压ADC
未学习 9.4 通过高压放大器保护低压ADC
-
 未学习 9.5 保护低压ADC-改进的解决方案
未学习 9.5 保护低压ADC-改进的解决方案
-
 未学习 9.6 用TVS二极管保护ADC
未学习 9.6 用TVS二极管保护ADC
-
 未学习 9.7 用TVS二极管保护ADC –改进的解决方案
未学习 9.7 用TVS二极管保护ADC –改进的解决方案
-
 未学习 10.1 了解和比较高速模数(ADC)和数模转换器(DAC)转换器架构
未学习 10.1 了解和比较高速模数(ADC)和数模转换器(DAC)转换器架构
-
 未学习 10.2 抖动对高速模数转换器(ADC)信噪比(SNR)的影响
未学习 10.2 抖动对高速模数转换器(ADC)信噪比(SNR)的影响
-
 未学习 10.3了解高速数据转换器中的信噪比(SNR)和噪声频谱密度(NSD)
未学习 10.3了解高速数据转换器中的信噪比(SNR)和噪声频谱密度(NSD)
-
 未学习 10.4 带宽与频率 - 子采样概念
未学习 10.4 带宽与频率 - 子采样概念
-
 未学习 10.5 高速数据转换器中的采样率与数据速率,抽取(DDC)和插值(DUC)概念
未学习 10.5 高速数据转换器中的采样率与数据速率,抽取(DDC)和插值(DUC)概念
-
 未学习 10.6 频率和采样率规划:了解高速ADC中的采样,奈奎斯特区,谐波和杂散性能
未学习 10.6 频率和采样率规划:了解高速ADC中的采样,奈奎斯特区,谐波和杂散性能
-
 未学习 10.7 高速数据转换器信号处理:真实和复杂的调制
未学习 10.7 高速数据转换器信号处理:真实和复杂的调制
-
 未学习 (中文)11.1 ADC 系统中的噪声
未学习 (中文)11.1 ADC 系统中的噪声
-
 未学习 (中文)11.3 ADC 噪声测量、方法和参数
未学习 (中文)11.3 ADC 噪声测量、方法和参数
-
 未学习 (中文)11.4 低速 Δ-Σ ADC 的系统噪声性能
未学习 (中文)11.4 低速 Δ-Σ ADC 的系统噪声性能
-
 未学习 (中文)11.5 分析和计算 ADC 系统中的噪声带宽——多级滤波器
未学习 (中文)11.5 分析和计算 ADC 系统中的噪声带宽——多级滤波器
-
 未学习 (中文)11.6 分析和计算 ADC 系统中的噪声带宽——数字滤波器
未学习 (中文)11.6 分析和计算 ADC 系统中的噪声带宽——数字滤波器
-
 未学习 (中文)11.7 增益对噪声、ADC FSR 和动态范围的影响
未学习 (中文)11.7 增益对噪声、ADC FSR 和动态范围的影响
-
 未学习 (中文)11.8 计算放大器 + ADC 总噪声:设计示例
未学习 (中文)11.8 计算放大器 + ADC 总噪声:设计示例
-
 未学习 (中文)11.9 ADC 系统中的参考噪声简介
未学习 (中文)11.9 ADC 系统中的参考噪声简介
-
 未学习 (中文)11.10 参考噪声对信号链性能的影响
未学习 (中文)11.10 参考噪声对信号链性能的影响
-
 未学习 (中文)11.11 降低参考噪声
未学习 (中文)11.11 降低参考噪声
-
 未学习 动手实验:放大器稳定和电荷桶滤波器设计
未学习 动手实验:放大器稳定和电荷桶滤波器设计
-
 未学习 无需放大器即可驱动 SAR ADC
未学习 无需放大器即可驱动 SAR ADC
-
 未学习 外部EOS保护装置
未学习 外部EOS保护装置
-
 未学习 (中文)5.5 实验 - 混叠和抗混叠滤波器
未学习 (中文)5.5 实验 - 混叠和抗混叠滤波器
-
 未学习 (中文)6.7 R-C组件选择背后的数学
未学习 (中文)6.7 R-C组件选择背后的数学
-
 未学习 (中文)7.1 电压基准概述
未学习 (中文)7.1 电压基准概述
-
 未学习 (中文)7.3 SAR 基准输入 - CDAC
未学习 (中文)7.3 SAR 基准输入 - CDAC
-
 未学习 (中文)7.4 了解SAR参考输入模型
未学习 (中文)7.4 了解SAR参考输入模型
-
 未学习 (中文)7.5 开发SAR输入参考模型
未学习 (中文)7.5 开发SAR输入参考模型
-
 未学习 (中文)7.6 驱动参考实验
未学习 (中文)7.6 驱动参考实验
-
 未学习 (中文)8.1 SAR ADC功率调节
未学习 (中文)8.1 SAR ADC功率调节
-
 未学习 (中文)8.2 动手实验 - 系统功率调节
未学习 (中文)8.2 动手实验 - 系统功率调节
-
 未学习 (中文)9.1 EOS和ESD
未学习 (中文)9.1 EOS和ESD
-
 未学习 (中文)9.3 向TINA 导入二极管PSpice模型
未学习 (中文)9.3 向TINA 导入二极管PSpice模型
-
 未学习 (中文)9.4 通过高压放大器保护低压ADC
未学习 (中文)9.4 通过高压放大器保护低压ADC
-
 未学习 (中文)9.5 保护低压ADC-改进的解决方案
未学习 (中文)9.5 保护低压ADC-改进的解决方案
-
 未学习 (中文)9.6 用TVS二极管保护ADC
未学习 (中文)9.6 用TVS二极管保护ADC
-
 未学习 (中文)9.7 用TVS二极管保护ADC –改进的解决方案
未学习 (中文)9.7 用TVS二极管保护ADC –改进的解决方案
-
 未学习 (中文)10.1 了解和比较高速模数(ADC)和数模转换器(DAC)转换器架构
未学习 (中文)10.1 了解和比较高速模数(ADC)和数模转换器(DAC)转换器架构
-
 未学习 (中文)10.2 抖动对高速模数转换器(ADC)信噪比(SNR)的影响
未学习 (中文)10.2 抖动对高速模数转换器(ADC)信噪比(SNR)的影响
-
 未学习 (中文)10.3 了解高速数据转换器中的信噪比(SNR)和噪声频谱密度(NSD)
未学习 (中文)10.3 了解高速数据转换器中的信噪比(SNR)和噪声频谱密度(NSD)
-
 未学习 (中文)10.4 带宽与频率 - 子采样概念
未学习 (中文)10.4 带宽与频率 - 子采样概念
-
 未学习 (中文)10.5 高速数据转换器中的采样率与数据速率,抽取(DDC)和插值(DUC)概念
未学习 (中文)10.5 高速数据转换器中的采样率与数据速率,抽取(DDC)和插值(DUC)概念
-
 未学习 (中文)10.6 频率和采样率规划:了解高速ADC中的采样,奈奎斯特区,谐波和杂散性能
未学习 (中文)10.6 频率和采样率规划:了解高速ADC中的采样,奈奎斯特区,谐波和杂散性能
-
 未学习 (中文)10.7 高速数据转换器信号处理:真实和复杂的调制
未学习 (中文)10.7 高速数据转换器信号处理:真实和复杂的调制
-
 未学习 (中文)了解 ADC 系统中的电源噪声
未学习 (中文)了解 ADC 系统中的电源噪声
-
 未学习 (中文)时钟噪声如何影响精密 ADC 测量
未学习 (中文)时钟噪声如何影响精密 ADC 测量
-
 未学习 (中文)电源噪声降低技术
未学习 (中文)电源噪声降低技术
-
 未学习 保护 Delta-Sigma ADC:RTD 概述
未学习 保护 Delta-Sigma ADC:RTD 概述
-
 未学习 保护 Delta-Sigma ADC:输入保护电路操作
未学习 保护 Delta-Sigma ADC:输入保护电路操作
-
 未学习 保护 Δ-Σ 元件选型
未学习 保护 Δ-Σ 元件选型
-
 未学习 利用 TVS 保护 Δ-Σ:性能影响
未学习 利用 TVS 保护 Δ-Σ:性能影响
-
 未学习 保护 Δ-Σ ADC:特殊输入范围
未学习 保护 Δ-Σ ADC:特殊输入范围
-
 未学习 PCB 布线阻抗匹配
未学习 PCB 布线阻抗匹配
-
 未学习 去耦电容
未学习 去耦电容
-
 未学习 SAR 和 Δ-Σ:噪声和驱动注意事项
未学习 SAR 和 Δ-Σ:噪声和驱动注意事项
-
 未学习 电磁兼容测试方法及标准
未学习 电磁兼容测试方法及标准
-
 未学习 3线RTD系统的挑战
未学习 3线RTD系统的挑战
-
 未学习 设计软件与硬件可配置的多 RTD 测量系统
未学习 设计软件与硬件可配置的多 RTD 测量系统
-
 未学习 混叠和抗混叠滤波器
未学习 混叠和抗混叠滤波器