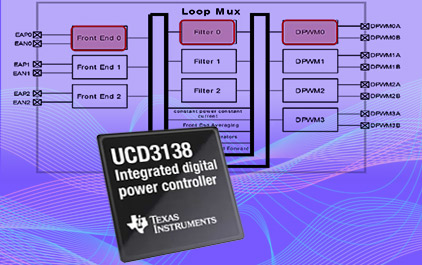
电源管理
最新课程
- MSPM0G 系列 MCU 时钟配置:在 LED 闪烁的情况下动手操作
- Code Composer Studio™ v20 入门
- 双 DMA 正弦波环回:在 MSPM0G 上实现从 DAC 生成到 ADC 捕捉
- MSPM0G3507 动态 CRC 配置和实时验证
- 视频系列:tiarmclang 编译器
- 汽车应用中的 Jacinto™ 7 处理器
- 可以在 2 分钟内实现无线基础设施应用
- TI 超声成像系统电源方案介绍
- TI 连续血糖监测(CGM)方案介绍
- AI 智能眼镜充电的需求与续航力
热门课程
1.3反激式变压器的铜损
大家好,我叫李思聪
是德州仪器高压小功率产品线的市场工程师
我要介绍的主题是如何优化变压器的设计
来改进反激式变换器的效率和 EMI 性能
现在介绍第三部分的内容
即反激式变压器的铜损
铜损主要是指变压器绕组的这个电阻引起的损耗
由于流过变压器绕组的这个电流
不是正弦波
所以它不但含有直流
还含有这个很多的这个高频谐波成分
例如一个流过这个变压器原边这个绕组电流
那么它的峰值是十安培
duty 是这个20%
那么这个电流经过傅里叶分析以后
它的这个直流成分是0.4安
基波的这个电流成分是0.8安
那么二次谐波是这个0.7安左右
三次谐波是0.5安左右
那么此外还有很多很多的高频谐波成分
那么这样同样的
对于流过变压器次级绕组的电流来说
也是存在很大一个高频谐波成分
那么所以呢
通常用直流电阻就 DCR 来表示
这个直流成分产生的损耗
用这个 ACR 就是交流电阻
来表示这些高频谐波产生的这个总的损耗
那么这个 ACR 跟 DCR 这个比值
可能是1到2之间
但是呢有时候还会更大
那么这个交流电阻跟直流电阻的比值
跟这个开关流过这个变压器电流
或者绕组这个电流的频率
以及绕组线的这个线径的大小
以及绕组的这个结构,层与层之间的结构有关系
引起交流电阻的损耗的原因
主要是涡流
那么涡流效应包括了三个部分
一个是集肤效应,邻近效应
还有气隙边缘效应
那么这种涡流效应
跟磁芯涡流损耗
跟涡流损耗相似
但是由于铜的导电率远远高于铁氧体的导电率
所以这种在铜里面引起的这个涡流损耗
会恶劣的多
首先介绍这个集肤效应
我们先看一下
如果是一个直流电流流过一条导线
那么在没有外磁场的作用下
这个电流密度在这个导线的截面积上
是均匀分布的
但是如果流过这个导线的电流
是这个交流的电流
那么由于交流电流会在这个导线上
或者周围产生交变的电磁场
交变的电磁场又切过导线截面积的时候
会产生这个涡流
涡流会使导线的中心位置
在中间的位置是相互抵消的
而在这个外表面上是相互加强了
那么从而导致这个电流
在这个导线的截面积上
分布密度是不均匀的
那么如这个图所示
那么通常用集肤深度
或者是穿透深度来表示集肤效应
即所谓的集肤深度跟穿透深度
是表示电流密度从外表面的1的地方
下降到这个
电流密度下降到 1/e 的这个时候
所作的长度
或者是这个直径
那么就叫做集肤深度
那么集肤深度可以用这个公式来计算
它跟这个导线电导率是成正比的
跟导线的磁导率
以及流过导线的电流频率是成反比的
对于铜
那么我们知道它的这个电导率
跟相对磁导率
那么我们可以算出它的集肤深度
2.4毫米除以这个根号的频率
这边列出了频率跟集肤深度关系的曲线图
我们可见当开关频率小于 100k 的时候
那么集肤深度的这个变化
是非常非常快的
当这个开关频率
或者是这个频率大于这个 400k 的时候
那么集肤深度的变化
已经变得很小了
这边一个例子
假设一个导线
它的这个直径是7个集肤深度
7个集肤深度
那么从这边来看
大部分的电流会在这个外表面
从外表面到这个
你看这个分布在这个
大部分的电流会分布在这个
从外表面到
往里走到两个集肤深度的
这个区域范围内
如果用这个导线来看的话
它这个交流电阻跟直流电阻的比值
大概可以算出是两倍
也就是交流电路是直流电阻的两倍
那么假设我们把这个
这个导线里面5个集肤深度截面积给挖掉
也就让导线变成是空的一个导线
那么这时候
由于这个对交流电阻来说
是一样它电流电阻是不变的
但对于直流电阻来说
这时候直流电阻减小了一倍
那么导致交流电阻跟直流电阻的比值
就变成了1
同样的,当两根线
或者更多的线放置在一起的时候
临近的导线所产生的磁场
就会影响这个导线的电荷的分布
或者电流密度的分布
那么通常来说
这个邻近效应会比集肤效应影响更恶劣
那么在这里为了分析的方便
我们通常都假设
导线的线径是大大于集肤深度
那么先以两根导线来说明
当这两根导线放在一起流过的电流相同的时候
由于邻近效应的作用
导线内的这个电流的分布
电流这个密度的分布是在
靠近导线的两个外表面上
当这个流过电流如果是相同的话
那么邻近效应就会使它这个电流分布
在两根导线相靠近的这个表面上
由于邻近效应
使这个电荷分布在更小的区域内
从而导致流过这个电流实际有效的面积减小
那么导致它这个电阻增大
那么损耗也就增大了
同样这边列出了
如果是一层的这个导线
流过电流是相同的情况下
它这个电流分布的大概一个示意图
这边展示了
这个如果绕组是两层的情况
那么如果电流上面一层跟下面一层的这个电流
那个方向是一样的
那么电流分布在上下的这两个表面上
如果这个上面一层跟下面一层电流方向是相反的话
电流就分布到了这个中间的表面上
总的来说,随着层数的增加
邻近效应对电流这个密度的分布的影响更严重
导线有效截面积变得更小
交流电阻变得更大
那么这样的话交流损耗就变得更大
对于一个多层的这个线圈的邻近效应
我们这边以一个反激式变压器的
原边绕组为例来说明
那么首先假设这个绕组的线径是大于集肤深度
原边绕组的匝数是24分为三层
均匀分布在这个窗口上
每层是 8 匝
我们假设流过线圈的电流为 I
那么因为每匝都是并联
每匝上面流过的静电流就是 I
我们是假设 I 等于一的话
那就是对这个总的磁动势来说就是24
由于气隙是开到了磁芯的下面的地方
对于第一层,在这个磁芯的下表面上
它的磁动势就是24
那么这个磁动势要最靠近磁芯的
就气隙下面这个磁芯的这一层的这个绕组来平衡
也就是说因为它有 8 匝
那么所以每匝上面产生的电流就是要有3安培
所以在这个下面要产生3安培的电流
那么实际上流过了电流只要1安培
那么所以呢
这个就会在线的内部会有2安培的回流
那么这个回流电流就是在这个上表面上
2安培的电流
那么在第二层的这个下表面
因为 Layer 1 层上面是2安培的电流
它同样要产生2安培的电流
来平衡下表面磁动势
在这个 Layer 2 层的表面就会产生2安培的电流
这实际流过的静电流就是 1 安培
就要有1安培的电流
要在这个上表面上
产生这个回流过来
这个回过来电流就实际上就是
会在这个表面上平衡
那么使 Layer 3 层上这个1安培电流
就都流在了这个下表面上
那么从这边可以看到
由于邻近效应
Layer 1 层上实际上有这个
电流上面分布的这个5安培的电流
那么其中4安培是在导线的内部做涡流的
那么 Layer 2 层上实际上流过了3安培的电流
有1安培在内部做涡流的
那么这些涡流都会导致这个电流
分布在这个更小的
而且是会把电流分布在这个比较这个线圈的表面上
那么使这个相当于来说相当于这个
对这个三层相当于这个交流电阻增加了19倍
所以呢这个损耗就大大增加了
如果我们添加更多的层有四层的话
那么相当于这个交流电阻
就会产生指数级的这个增大
那么如果是四层就可以得到44倍的这个增大
如果是五层的话
那么就可能变成了85倍的这个增大
当然这只是用一个简单的方法
来说明这个邻近效应的一个效果
实际上电流的分布要比这个复杂得很多
先懂得原理
邻近效应也会引起其他不导电绕组产生涡流
从而产生这个铜损
这边以一个三明治绕法的反激式变压器为例
当这个原边绕组流过电流的时候
那副边绕组是不流过电流
但是由于邻近效应的影响
当原边绕组流过电流的时候
会在副边绕组上感应出一个电流
那么这个是个涡流
那么这个涡流就会在电阻内部上产生一个损耗
那么当然这个是一个副边绕组的一个例子
实际上也可能会在
例如这个变压器中间的这个屏蔽层
或者是其它一些辅助绕组上
都会产生相同的这种邻近效应
通常以邻近效应因子 KP
也就是线圈交流电阻与直流电阻的比值
来评估邻近效应
那么这也就是 Dowell 的这个方程式
那么 Dowell 推导出了
KP 跟这个 Q 以及绕组层数的一个关系
那么这其中 Q 是指层的这个厚度
跟这个穿透深度的一个比值
那么层的厚度并不是指
圆形线的这个线径
而是指跟这个圆形线
具有相同截面积的这个方形块的这个长
那么所以这之间涉及到一个转换系数
那么这转换系数就是层的厚度是等于0.886倍线径
那么从这个 Dowell 这个方程式画出了这个关系曲线
我们可以看出
层数越多,那么这个 KP
也就是 RAC 除以 RDC 的值就越大
那么当然我们可以通过减小 Q 值
也就是减少这个层的厚度
与这个穿透深度的这个比值
来减少这个 KP 值
但是这里面有个问题
就是减小这个 Q 也就减少这个层厚度
那么就意味着减少这个线径
那么减少线径它的直流电阻就增大了
虽然说这个交流电阻除以直流电阻的比值减小了
但是呢这个直流电阻增大了
那么总的来说这个交流电阻可能也变得很大
所以说这无法确定整个铜损是否减小了
那么也就是意味着 Dowell 这个方程式
它这个画出曲线
它并不适合指导如优化的去设计层数与线径
那么此外 Dowell 处理做这个仿真的时候
那么只处理采用的是正弦波
而不是这个方波
所以呢所有结果也不是非常的准确
在参考文献三中
Bruce Carsten 在 Dowell 的基础上做了一些改进
然后提出了归一化的等效电阻系数
来表达邻近效应的影响
那么他做了两个改进
一个是用 duty 为50%的三角波来代替正弦波
第二个就在计算这个等效电阻的时候
它不是采用直流电阻
而是采用这个基波频率下 Q 等于1时
的等效电阻来归一化这个交流电阻
那么由 Bruce Carsten 这个公式
推导这个公式画出 KR 跟层数
以及 Q 的关系的曲线
如这个图所示
那么从这边来看
对于任一个层数都有一个 KR 的谷点
那么这个 KR 的谷点对应的这个 Q 值
实际上就是最优化的层的厚度的值
或者是说层的厚度跟集肤深度的比例的值
由此我们可以根据这个值
来选出这个线的这个最优化的线的直径
在参考文献五中也做了类似的研究
那么得出非常相似的结果
所以都是非常有用的
最后我们来聊一下这个利兹线跟多股线
对于单股的实心线来说
它对这个直流电阻是有好处的
因为它可以使这个截面积最大化
从而最大限度的降低这个接入电阻
但是在高频线情况下
我们前面分析的因为邻近效应的影响
它的交流电阻会变得非常的大
为了解决这个矛盾的话
我们可以使用多股线或者利兹线
对于一根直径为 D 的单股线
它可以有四根直径为1/2的这个线来这个代替
那么它们具有相同的这个直流电阻
但是它交流电阻就大大降低了
同样的我们可以用这个15根
直径为 1/5 D 的线来代替
那么这时他的直流电阻是原来
这个单根线直流电阻的1.67倍
但是它交流电阻也会大大的减少
也可以用这个65股的这个线
每股是1/10这个线径来代替
那么这根线就相当于一个利兹线
那么它的直流电阻是原来这个线的1.54倍
交流电阻可以大大的降低
对于这种类似利兹线
它实际上相当于一个多层的并联的绕组
那么它之间也有邻近效应的影响
那么怎样去选择这个线径与股数
我们可以用前面介绍了 Carsten 的这个曲线
或者方程式来选择利兹线的股数
以及这个它的线径
利兹线的优势是它具有非常好的
这个虽然非常小的交流电阻
同时它的直流电阻也很小
但是利兹线的缺点是它成本很高
难以处理和焊接
窗口的利用率比较差
这边列出了参考文献
大家如果有兴趣可以去下载
谢谢大家
-
 未学习 1.1 碳化硅和氮化镓器件的介绍, 应用及优势
未学习 1.1 碳化硅和氮化镓器件的介绍, 应用及优势
-
 未学习 1.2 驱动器设计考虑
未学习 1.2 驱动器设计考虑
-
 未学习 1.3 开关性能
未学习 1.3 开关性能
-
 未学习 1.4 硬开关,软开关案例
未学习 1.4 硬开关,软开关案例
-
 未学习 1.5 测量
未学习 1.5 测量
-
 未学习 1.6 仿真及总结
未学习 1.6 仿真及总结
-
 未学习 1.1 TI PMBus简介课程
未学习 1.1 TI PMBus简介课程
-
 未学习 1.2 TI PMBus简介课程(一)
未学习 1.2 TI PMBus简介课程(一)
-
 未学习 1.3 TI PMBus简介课程(二)
未学习 1.3 TI PMBus简介课程(二)
-
 未学习 1.4 TI PMBus简介课程(三)
未学习 1.4 TI PMBus简介课程(三)
-
 未学习 USB Type C介绍
未学习 USB Type C介绍
-
 未学习 USB PD介绍
未学习 USB PD介绍
-
 未学习 45W单端口AC/DC方案介绍
未学习 45W单端口AC/DC方案介绍
-
 未学习 45W双端口AC/DC方案介绍
未学习 45W双端口AC/DC方案介绍
-
 未学习 1.1高频降压变化器的局限
未学习 1.1高频降压变化器的局限
-
 未学习 1.2串联电容降压变换器的工作模式
未学习 1.2串联电容降压变换器的工作模式
-
 未学习 1.3串联电容降压变换器的工作模式续
未学习 1.3串联电容降压变换器的工作模式续
-
 未学习 1.4串联电容降压变换器的主要优点
未学习 1.4串联电容降压变换器的主要优点
-
 未学习 1.5串联电容降压变换器的测试结果
未学习 1.5串联电容降压变换器的测试结果
-
 未学习 1.6串联电容降压变换器的设计要点
未学习 1.6串联电容降压变换器的设计要点
-
 未学习 1.7串联电容降压变换器的PCB
未学习 1.7串联电容降压变换器的PCB
-
 未学习 1.1反激式变压器的概论
未学习 1.1反激式变压器的概论
-
 未学习 1.2反激式变压器的磁心损耗
未学习 1.2反激式变压器的磁心损耗
-
 未学习 1.3反激式变压器的铜损
未学习 1.3反激式变压器的铜损
-
 未学习 1.4反激式变压器的漏感和嵌位电压
未学习 1.4反激式变压器的漏感和嵌位电压
-
 未学习 1.5减小反激式变压器的EMI性能
未学习 1.5减小反激式变压器的EMI性能
-
 未学习 双向DC-DC 变换器拓扑的对比与设计(1) – 应用概览
未学习 双向DC-DC 变换器拓扑的对比与设计(1) – 应用概览
-
 未学习 双向DC-DC 变换器拓扑的对比与设计(2) – 拓扑比较
未学习 双向DC-DC 变换器拓扑的对比与设计(2) – 拓扑比较
-
 未学习 双向DC-DC 变换器拓扑的对比与设计(3) – UCD3138控制方案
未学习 双向DC-DC 变换器拓扑的对比与设计(3) – UCD3138控制方案
-
 未学习 双向DC-DC 变换器拓扑的对比与设计(4) – 测试结果的比较
未学习 双向DC-DC 变换器拓扑的对比与设计(4) – 测试结果的比较
-
 未学习 双向DC-DC 变换器拓扑的对比与设计(5) – 性能及总结
未学习 双向DC-DC 变换器拓扑的对比与设计(5) – 性能及总结
-
 未学习 电源系统设计工具
未学习 电源系统设计工具
-
 未学习 工业及汽车系统的低EMI电源变换器设计(一)课程概览
未学习 工业及汽车系统的低EMI电源变换器设计(一)课程概览
-
 未学习 工业及汽车系统的低EMI电源变换器设计(二)工业及汽车运用DCDC的主要特点
未学习 工业及汽车系统的低EMI电源变换器设计(二)工业及汽车运用DCDC的主要特点
-
 未学习 工业及汽车系统的低EMI电源变换器设计(三)降低开关电源EMI干扰的方法
未学习 工业及汽车系统的低EMI电源变换器设计(三)降低开关电源EMI干扰的方法
-
 未学习 工业及汽车系统的低EMI电源变换器设计(四)通过优化PCB layout 有效降低EMI
未学习 工业及汽车系统的低EMI电源变换器设计(四)通过优化PCB layout 有效降低EMI
-
 未学习 工业及汽车系统的低EMI电源变换器设计(五)通过控制开关点的Slew Rate有效降低EMI
未学习 工业及汽车系统的低EMI电源变换器设计(五)通过控制开关点的Slew Rate有效降低EMI
-
 未学习 工业及汽车系统的低EMI电源变换器设计(六)通过频率抖动有效降低EMI
未学习 工业及汽车系统的低EMI电源变换器设计(六)通过频率抖动有效降低EMI
-
 未学习 工业及汽车系统的低EMI电源变换器设计(七)通过增加EMI 滤波器有效降低EMI
未学习 工业及汽车系统的低EMI电源变换器设计(七)通过增加EMI 滤波器有效降低EMI
-
 未学习 工业及汽车系统的低EMI电源变换器设计(八)— EMI 优化技巧小结
未学习 工业及汽车系统的低EMI电源变换器设计(八)— EMI 优化技巧小结
-
 未学习 1.1 开关模式电源转换器补偿简单易行 — 补偿的原因和目的
未学习 1.1 开关模式电源转换器补偿简单易行 — 补偿的原因和目的
-
 未学习 1.2 开关模式电源转换器补偿简单易行 —零点和极点
未学习 1.2 开关模式电源转换器补偿简单易行 —零点和极点
-
 未学习 1.3 开关模式电源转换器补偿简单易行 —功率级第一部分
未学习 1.3 开关模式电源转换器补偿简单易行 —功率级第一部分
-
 未学习 1.4 开关模式电源转换器补偿简单易行 —功率级第二部分
未学习 1.4 开关模式电源转换器补偿简单易行 —功率级第二部分
-
 未学习 1.5 开关模式电源转换器补偿简单易行 —反馈回路介绍
未学习 1.5 开关模式电源转换器补偿简单易行 —反馈回路介绍
-
 未学习 1.6 开关模式电源转换器补偿简单易行 —补偿实例
未学习 1.6 开关模式电源转换器补偿简单易行 —补偿实例
-
 未学习 1.7 开关模式电源转换器补偿简单易行 —实际应用限制和常见问题第一部分
未学习 1.7 开关模式电源转换器补偿简单易行 —实际应用限制和常见问题第一部分
-
 未学习 1.8 开关模式电源转换器补偿简单易行 —实际应用限制和常见问题第二部分
未学习 1.8 开关模式电源转换器补偿简单易行 —实际应用限制和常见问题第二部分
-
 未学习 1.1 升降压变换器的应用,实现方式和拓扑
未学习 1.1 升降压变换器的应用,实现方式和拓扑
-
 未学习 1.2 LM5175控制的升降压变换器工作原理
未学习 1.2 LM5175控制的升降压变换器工作原理
-
 未学习 1.3 设计举例
未学习 1.3 设计举例
-
 未学习 1.4 PCB板布局介绍
未学习 1.4 PCB板布局介绍
-
 未学习 无线传输功率(1)
未学习 无线传输功率(1)
-
 未学习 无线传输功率(2)
未学习 无线传输功率(2)
-
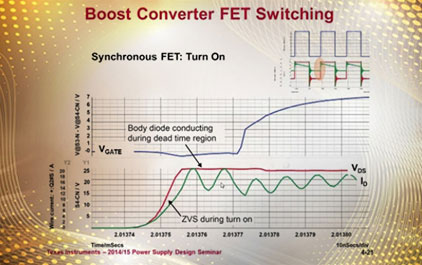 未学习 多相同步升压型变换器(1)
未学习 多相同步升压型变换器(1)
-
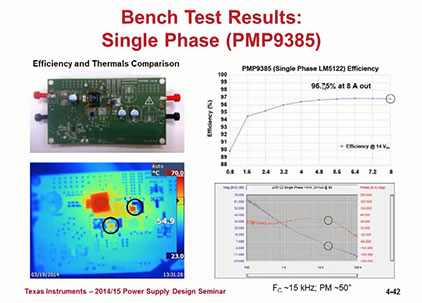 未学习 多相同步升压型变换器(2)
未学习 多相同步升压型变换器(2)
-
 未学习 小功率的AC/DC变换器的控制难题(1)
未学习 小功率的AC/DC变换器的控制难题(1)
-
 未学习 小功率的AC/DC变换器的控制难题(2)
未学习 小功率的AC/DC变换器的控制难题(2)
-
 未学习 德州仪器电源新产品
未学习 德州仪器电源新产品
-
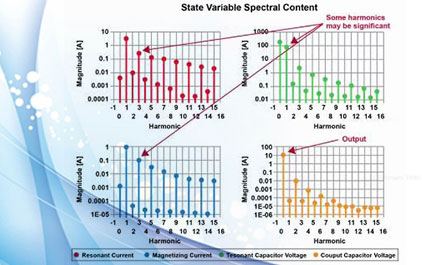 未学习 LLC 变换器小信号模型分析(上)
未学习 LLC 变换器小信号模型分析(上)
-
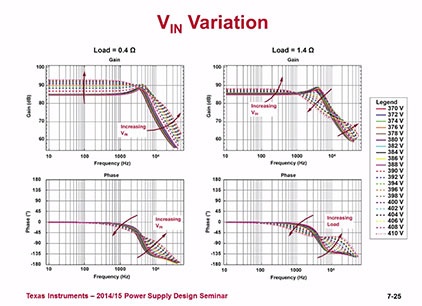 未学习 LLC 变换器小信号模型分析(下)
未学习 LLC 变换器小信号模型分析(下)
-
 未学习 基于氮化镓的图腾柱无桥 PFC(CCM)(上)
未学习 基于氮化镓的图腾柱无桥 PFC(CCM)(上)
-
 未学习 基于氮化镓的图腾柱无桥 PFC(CCM)(下)
未学习 基于氮化镓的图腾柱无桥 PFC(CCM)(下)
-
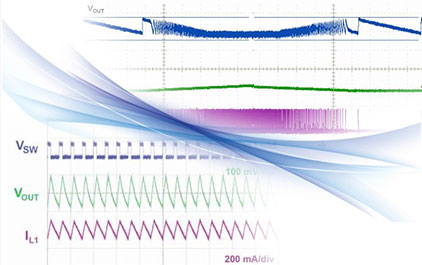 未学习 变频降压型变换器的控制策略(上)
未学习 变频降压型变换器的控制策略(上)
-
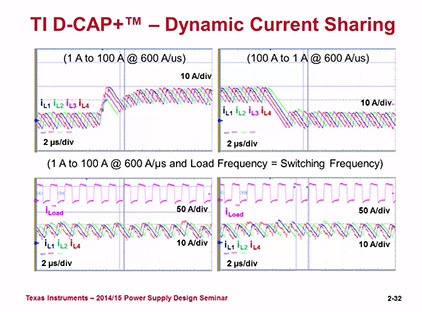 未学习 变频降压型变换器的控制策略(下)
未学习 变频降压型变换器的控制策略(下)
-
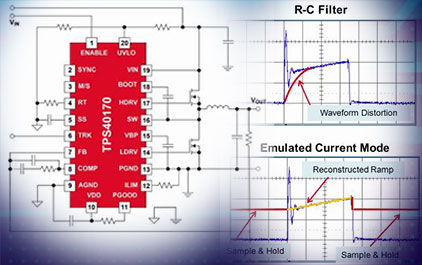 未学习 定频降压型变换器的控制策略(上)
未学习 定频降压型变换器的控制策略(上)
-
 未学习 定频降压型变换器的控制策略(下)
未学习 定频降压型变换器的控制策略(下)