通用运算放大器
最新课程
- MSPM0G 系列 MCU 时钟配置:在 LED 闪烁的情况下动手操作
- Code Composer Studio™ v20 入门
- 双 DMA 正弦波环回:在 MSPM0G 上实现从 DAC 生成到 ADC 捕捉
- MSPM0G3507 动态 CRC 配置和实时验证
- 视频系列:tiarmclang 编译器
- 汽车应用中的 Jacinto™ 7 处理器
- 可以在 2 分钟内实现无线基础设施应用
- TI 超声成像系统电源方案介绍
- TI 连续血糖监测(CGM)方案介绍
- AI 智能眼镜充电的需求与续航力
热门课程
5.4 TI 高精度实验室 - 带宽 4
大家好
欢迎来到 TI Precision Labs
德州仪器高精度实验室
本次视频将介绍
运算放大器的 Bandwidth 带宽的第四部分
我们将讨论五个带宽相关的主题
第一 深入讨论 Aol 曲线的斜率
如何影响增益带宽
第二 为何运算放大器的输入电容能够限制带宽
第三 如何计算放大器电路的实际增益与带宽
第四 如何运用 feedback capacitor
来限制电路的带宽
第五 了解 slew rate 即压摆率
它是如何影响不同带宽的响应的
我们已经很详细的讨论了增益带宽积
我们知道只有当 AOL 曲线的斜率
为 -20dB/dec 时是有效的
不幸的是有时增益带宽积
是有效还是无效不是很明显
下面由 OPA209 数据表的增益带宽积规格
典型的增益带宽积列出当增益为 1V/V 时
带宽为18MHz
但是其它闭回路增益的带宽呢
数据表中我们有开回路增益
相位曲线与频率
开回路增益曲线似乎是线性的
以 -20dB/dec 的恒定速率下降
因此大家可能会认为增益带宽积
适用于所有增益
然而仿真和实际测量将表示
这假设是不正确的
为什么呢先前我们假设开回路增益曲线有
-20dB/dec 的恒定斜率
然而我们发现由于有一对零点极点
在 1MHz 和 10MHz 之间
AOL 曲线有一个转折
接近以 1MHz 的极点
在很小的频率范围内
造成开回路增益下降的斜率大于 -20dB/dec
不过极点很快速地被零点补偿
由于对数坐标是不可能
在 AOL 曲线看到这个小弯曲的
事实上 此弯曲可能比曲线的厚度还小
在曲线的弯曲处放大
你会发现 1V/V 的增益下
增益带宽为 18MHz
但当闭回路增益大于 20dB
带宽增大到 23.7 MHz
然而发现 AOL 曲线的弯曲是困难的
在相位曲线发现零点极点较为明显
请注意 在 1MHz 附近的相位曲线倾角
这是由于有零点极点对的缘故
因此建议大家
除了检查运算放大器数据表中的增益曲线
也要检查相位曲线
这两条曲线
描述增益带宽积是如何随频率 闭回路增益变化
请注意在 0dB 或 1V/V 的闭回路增益时
在数据表所列增益带宽积为 18MHz
当闭回路增益增加
带宽增加至 23.7MHz
最终这个讨论学习到三件事情
第一 看到增益带宽在不同闭环回路增益有些偏差
是不常见的
是不常见的
而该偏差量将取决于放大器而异
第二 寻找一个零点极点 相位曲线是关键
第二 寻找一个零点极点 相位曲线是关键
所以除了检查开回路增益曲线
也要检查相位曲线
最后不要指望在数据表中列出带宽性能的确切性
因为典型带宽规格在不同的制程
约有正负 30% 和不同的温度下正负 30% 的变异
因此强烈建议设计时对 Bandwidth
要留显著的裕度
至此 我们已经看到
运算放大器的增益带宽如何限制带宽
然而在某些情况下
其它因素也可能影响带宽
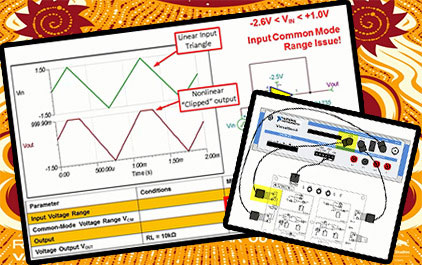
此页着重于输入电容对带宽的影响
所有运算放大器有差模和共模输入电容和阻抗
这种寄生电容是由于输入极电晶管的
半导体界面造成的
差模电容之间连接到两个输入端
共模电容被连接在各输入相对于交流接地
表格上通常显示了输入电容
在这个例子中
差模电容是 1.6pF
以及共模电容是 6.4pF
输入电容都比较小
所以你是不可能会看到带宽的限制
除非输入信号源具有大的串联电阻
在这个例子中
信号源电阻是比较大的 1M 欧姆
源电阻和共模输入电容组成低通滤波器
对应的截止频率为 24.87kHz
请注意 差模电容和反相输入端的共模电容
未包括在带宽计算
这是因为运算放大器的回授消除了这些电容
输入电容是 TI 的运算放大器模型的一部分
所以让我们来看看仿真的结果吧
此页是显示了 OPA192 交流传输特性
根据元件的增益带宽和 100V/V 的闭回路增益
我们预估带宽为 100kHz
但是我们的仿真只产生 24.46kHz带宽
这种差异是由于 1M 欧姆源电阻
和 6.4pF 共模输入电容构成的低通滤波器
在这个例子中
24.87kHz 手算带宽
与仿真 24.6kHz 的带宽相近
现在让我们讨论
如何计算运算放大器电路的实际增益
假设一个放大器电路的闭回路增益是定值
直到它开始在截止频率处下降
现实中闭回路增益在截止频率之前开始降低
通过这种衰减的误差通常是不可预期的
闭回路增益在任何频率可使用此公式
其中 f 表示频率
Gcl_dc 表示 DC 闭回路增益
fdom 表示主极点
β 表示回授因子
Aol_dc 表示 DC 开回路增益
让我们将这个公式应用于 OPA192 电路
闭回路直流增益是使用 126 分贝
这是 OPA192 数据表中的 AOL 规范
回授系数或 β 从 OPA192 电路中计算
主极点适用此方程式计算
于先前的带宽视频有提及
现在我们已经计算出闭回路直流增益和主极点频率
我们可以使用给定公式
来计算 10kHz 的闭回路增益
注意 电路带宽为 100kHz
因此 10kHz 时是稳定的放大器带宽
此例子中手算的闭回路增益是 99.5V/V
与仿真的闭回路增益 95.56V/V 相符
计算闭回路增益 DC 产生 99.995V/V
更接近 100V/V 理论值
因此我们可以得出结论
随着频率的增加
当你接近截止频率时
闭回路增益减少
所以如果需要设计一个在高频精确的增益
截止频率应相对应增加
到目前为止
确定电路的带宽时
我们已考虑内部运算放大器的规格
如增益带宽和输入电容
在某些情况下
使用外部元件来限制带宽较为理想
一种方法是使用主动滤波器
使用复杂的 RC 组合
以创造非常有效的滤波器
主动滤波器将在一个单独系列的视频进行讨论
限制电路的带宽
简单的方法是通过放置一个电容在回授路径
这种分析 想像低频时电容开路
高频时电容短路
在低频时可以忽略电容
因此增益为 100V/V 或 40dB
在高频时电容短路
而电流不会通过就是 9k 欧姆
因此电路为 1V/V 或 0dB 增益
在低频和高频之间增益将以
-20dB/dec 的速率下降
需要注意的是在非常高的频率
增益将进一步衰退
因为放大器带宽的限制
注意该滤波器的截止频率
是由回授电容和回授电阻求得
计算出的值是 1.005kHz
与 989Hz 的仿真值相符
值得注意的是
滤波器的增益从是 40dB 降低为 0dB
衰减是相依于放大器的增益
让我们来仔细看看此现象
此页比较回授电容滤波器
是用在高或低增益放大器
在这两种情况下的截止频率
已被设定为相同的值
如前面所及
在高频回授电容滤波器
在高频回授电容滤波器
有效的短路了回授电阻
有效的短路了回授电阻
使增益为 1V/V
因此回授电容滤波器
始终将直流电流值的增益降为 1
因此在滤波器的最大衰减量等于直流增益
在高增益电路情况下
增益从 100V/V 衰减至 1V/V 或 40dB
但是低增益电路只有衰减 6dB 的增益
重点是回授电容滤波器
在高增益电路是最有效
如果你需要一个有效的滤波器用于低增益电路
你应该研究主动滤波器
一般情况下
主动滤波器比回授电容滤波更有效
但回授电容滤波器很受欢迎
因为它们便宜 且简单
最后让我们讨论 Slew rate 压摆率
及 full power bandwidth 全功率带宽
运算放大器的 Slew rate
是输出信号的最大变化率
如果您有兴趣了解 Slew rate
请观看 Slew rate 视频系列
一个元件的 Slew rate
可以影响在不同频率下运算放大器的行为
此作用可以被误解为带宽限制
事实上最大输出电压与频率取决于 Slew rate
通常被称为全功率带宽
让我们来看看 OPA192 在全功率带宽
是如何影响两个不同的信号
当应用为 unit gain follower
最大输出电压与频率关系的图表显示
在给定频率的最大不失真 P2P 输出
例如 在 1MHz 1Vpk 信号
此信号是远低于最大输出限制
所以不会失真
然而在 1MHz 10Vpk 信号
是在全功率带宽以外
所以信号会失真
现在让我们来看看一个时域仿真
在这两种情况下的输出
此页显示了输入频率为 1MHz 10Vpk 及 1Vpk
OPA192 输出
注意 对于 1Vpk 输入预期有 1Vpk 的输出
1Vpk 输出通常不会出现失真
但是当 10Vpk 输入 输出却是 5Vpk
结果非常失真
事实上输出看起来更像是一个三角波
不是正弦波
这通常是放大器在 slew rate 限制的情况
基于上一页的 full power bandwidth 图形
就能理解此结果
最后一件事要注意的是输入信号
在 OPA192 buffer 带宽内
slew rate limitation 衰减了输出信号
此原因被不正确地解释为带宽限制
为了避免这个问题
请确保你的输出信号的幅值
不违反最大输出与频率的关系
总结 此视频讨论 AOL 曲线的斜率
如何影响增益带宽
运算放大器的输入电容
计算电路的实际增益
slew rate limitation
以及一些实现运算放大器滤波器的方法
感谢您的时间
请尝试测验来检查您对视频内容的理解吧
-
 未学习 1.1 TI 高精度实验室 - 介绍
未学习 1.1 TI 高精度实验室 - 介绍
-
 未学习 1.2 TI 高精度实验室 - 国家仪器虚拟测试仪概述
未学习 1.2 TI 高精度实验室 - 国家仪器虚拟测试仪概述
-
 未学习 2.1 TI 高精度实验室 - 输入失调电压与输入偏置电流
未学习 2.1 TI 高精度实验室 - 输入失调电压与输入偏置电流
-
 未学习 2.2 TI 高精度实验室 - 输入失调电压与输入偏置电流 实验
未学习 2.2 TI 高精度实验室 - 输入失调电压与输入偏置电流 实验
-
 未学习 3.1 TI 高精度实验室 - 输入输出限制
未学习 3.1 TI 高精度实验室 - 输入输出限制
-
 未学习 3.2 输入和输出限制 2
未学习 3.2 输入和输出限制 2
-
 未学习 3.3 输入和输出限制 3
未学习 3.3 输入和输出限制 3
-
 未学习 3.4 TI 高精度实验室 - 输入输出限制 实验
未学习 3.4 TI 高精度实验室 - 输入输出限制 实验
-
 未学习 4.1 功率与温度
未学习 4.1 功率与温度
-
 未学习 5.1 TI 高精度实验室 - 带宽 1
未学习 5.1 TI 高精度实验室 - 带宽 1
-
 未学习 5.2 TI 高精度实验室 - 带宽 2
未学习 5.2 TI 高精度实验室 - 带宽 2
-
 未学习 5.3 TI 高精度实验室 - 带宽 3
未学习 5.3 TI 高精度实验室 - 带宽 3
-
 未学习 5.4 TI 高精度实验室 - 带宽 4
未学习 5.4 TI 高精度实验室 - 带宽 4
-
 未学习 5.5 TI 高精度实验室 - 带宽 实验
未学习 5.5 TI 高精度实验室 - 带宽 实验
-
 未学习 6.1 TI 高精度实验室 - 压摆率 1
未学习 6.1 TI 高精度实验室 - 压摆率 1
-
 未学习 6.2 TI 高精度实验室 - 压摆率 2
未学习 6.2 TI 高精度实验室 - 压摆率 2
-
 未学习 6.3 TI 高精度实验室 - 压摆率 3
未学习 6.3 TI 高精度实验室 - 压摆率 3
-
 未学习 6.4 TI 高精度实验室 - 压摆率 实验
未学习 6.4 TI 高精度实验室 - 压摆率 实验
-
 未学习 7.1 共模抑制
未学习 7.1 共模抑制
-
 未学习 7.2 电源抑制
未学习 7.2 电源抑制
-
 未学习 8.1 TI 高精度实验室 - 噪声 1
未学习 8.1 TI 高精度实验室 - 噪声 1
-
 未学习 8.2 TI 高精度实验室 - 噪声 2
未学习 8.2 TI 高精度实验室 - 噪声 2
-
 未学习 8.3 TI 高精度实验室 - 噪声 3
未学习 8.3 TI 高精度实验室 - 噪声 3
-
 未学习 8.4 TI 高精度实验室 - 噪声 4
未学习 8.4 TI 高精度实验室 - 噪声 4
-
 未学习 8.5 TI 高精度实验室 - 噪声 5
未学习 8.5 TI 高精度实验室 - 噪声 5
-
 未学习 8.6 TI 高精度实验室 - 噪声 6
未学习 8.6 TI 高精度实验室 - 噪声 6
-
 未学习 8.7 TI 高精度实验室 - 噪声 7
未学习 8.7 TI 高精度实验室 - 噪声 7
-
 未学习 8.8 TI 高精度实验室 - 噪声 8
未学习 8.8 TI 高精度实验室 - 噪声 8
-
 未学习 8.9 TI 高精度实验室 - 噪声 实验
未学习 8.9 TI 高精度实验室 - 噪声 实验
-
 未学习 9.1 低失真运算放大器的设计-1
未学习 9.1 低失真运算放大器的设计-1
-
 未学习 9.2 低失真运算放大器的设计-2
未学习 9.2 低失真运算放大器的设计-2
-
 未学习 9.3 低失真运算放大器的设计-3
未学习 9.3 低失真运算放大器的设计-3
-
 未学习 9.4 低失真运算放大器的设计-4
未学习 9.4 低失真运算放大器的设计-4
-
 未学习 10.1 TI 高精度实验室 - 运算放大器:稳定性分析 1
未学习 10.1 TI 高精度实验室 - 运算放大器:稳定性分析 1
-
 未学习 10.2 TI 高精度实验室 - 运算放大器:稳定性分析 2
未学习 10.2 TI 高精度实验室 - 运算放大器:稳定性分析 2
-
 未学习 10.3 TI 高精度实验室 - 运算放大器:稳定性分析 3
未学习 10.3 TI 高精度实验室 - 运算放大器:稳定性分析 3
-
 未学习 10.4 TI 高精度实验室 - 运算放大器:稳定性分析 4
未学习 10.4 TI 高精度实验室 - 运算放大器:稳定性分析 4
-
 未学习 10.5 TI 高精度实验室 - 运算放大器:稳定性分析 5
未学习 10.5 TI 高精度实验室 - 运算放大器:稳定性分析 5
-
 未学习 10.6 TI 高精度实验室 - 运算放大器:稳定性分析 6
未学习 10.6 TI 高精度实验室 - 运算放大器:稳定性分析 6
-
 未学习 10.7 TI 高精度实验室 - 运算放大器:稳定性 - 实验
未学习 10.7 TI 高精度实验室 - 运算放大器:稳定性 - 实验
-
 未学习 11.1 TI 高精度实验室 - 静电释放 (ESD)
未学习 11.1 TI 高精度实验室 - 静电释放 (ESD)
-
 未学习 12.1 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 1
未学习 12.1 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 1
-
 未学习 12.2 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 2
未学习 12.2 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 2
-
 未学习 12.3 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 3
未学习 12.3 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 3
-
 未学习 12.4 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 4
未学习 12.4 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 4
-
 未学习 13.1 电流反馈型运算放大器
未学习 13.1 电流反馈型运算放大器
-
 未学习 13.2 电流反馈运放
未学习 13.2 电流反馈运放
-
 未学习 14.1 如何分析合成器相位噪声
未学习 14.1 如何分析合成器相位噪声
-
 未学习 15.1 全差分放大器 — 差分信号和FDA的介绍
未学习 15.1 全差分放大器 — 差分信号和FDA的介绍
-
 未学习 15.2 全差分放大器 — FDA的输入输出和共模
未学习 15.2 全差分放大器 — FDA的输入输出和共模
-
 未学习 15.3 全差分放大器 — FDA的稳定性和相位裕量
未学习 15.3 全差分放大器 — FDA的稳定性和相位裕量
-
 未学习 15.4 全差分放大器 — FDA的噪声和噪声控制
未学习 15.4 全差分放大器 — FDA的噪声和噪声控制
-
 未学习 15.5 全差分放大器 — 设计用于驱动差分输入ADC的前端电路
未学习 15.5 全差分放大器 — 设计用于驱动差分输入ADC的前端电路
-
 未学习 (中文)3.2 输入和输出限制 2
未学习 (中文)3.2 输入和输出限制 2
-
 未学习 (中文)14.3 电流反馈型运算放大器 Spice 仿真
未学习 (中文)14.3 电流反馈型运算放大器 Spice 仿真
-
 未学习 (中文)15.5 设计用于驱动差分输入ADC的前端电路
未学习 (中文)15.5 设计用于驱动差分输入ADC的前端电路
-
 未学习 运算放大器失真:简介
未学习 运算放大器失真:简介
-
 未学习 (中文)反相输入电容
未学习 (中文)反相输入电容
-
 未学习 (中文)断开差分放大器上的环路
未学习 (中文)断开差分放大器上的环路
-
 未学习 (中文)带宽 - 波特图截止频率
未学习 (中文)带宽 - 波特图截止频率
-
 未学习 (中文)带宽 - 增益和 GBW
未学习 (中文)带宽 - 增益和 GBW
-
 未学习 (中文)带宽 - 同相增益和极点
未学习 (中文)带宽 - 同相增益和极点
-
 未学习 (中文)带宽 - AOL 增益转换率
未学习 (中文)带宽 - AOL 增益转换率
-
 未学习 (中文)带宽 - 实验
未学习 (中文)带宽 - 实验
-
 未学习 (中文)转换率介绍
未学习 (中文)转换率介绍
-
 未学习 (中文)稳定时间
未学习 (中文)稳定时间
-
 未学习 (中文)信号响应
未学习 (中文)信号响应
-
 未学习 (中文)运算放大器失真:简介
未学习 (中文)运算放大器失真:简介
-
 未学习 (中文)输入级
未学习 (中文)输入级
-
 未学习 (中文)光谱密度
未学习 (中文)光谱密度
-
 未学习 (中文)计算 RMS 噪声
未学习 (中文)计算 RMS 噪声
-
 未学习 (中文)计算总噪声
未学习 (中文)计算总噪声
-
 未学习 (中文)简化计算
未学习 (中文)简化计算
-
 未学习 (中文)噪声spice模拟
未学习 (中文)噪声spice模拟
-
 未学习 (中文)验证噪声模型
未学习 (中文)验证噪声模型
-
 未学习 (中文)测量系统噪声
未学习 (中文)测量系统噪声
-
 未学习 (中文)1/F 噪声
未学习 (中文)1/F 噪声
-
 未学习 (中文)噪声 - 实验
未学习 (中文)噪声 - 实验
-
 未学习 理想的无源元件
未学习 理想的无源元件