通用运算放大器
最新课程
- MSPM0G 系列 MCU 时钟配置:在 LED 闪烁的情况下动手操作
- Code Composer Studio™ v20 入门
- 双 DMA 正弦波环回:在 MSPM0G 上实现从 DAC 生成到 ADC 捕捉
- MSPM0G3507 动态 CRC 配置和实时验证
- 视频系列:tiarmclang 编译器
- 汽车应用中的 Jacinto™ 7 处理器
- 可以在 2 分钟内实现无线基础设施应用
- TI 超声成像系统电源方案介绍
- TI 连续血糖监测(CGM)方案介绍
- AI 智能眼镜充电的需求与续航力
热门课程
6.1 TI 高精度实验室 - 压摆率 1
大家好
欢迎来到 TI Precision Labs
德州仪器高精度实验室
本次视频将会探讨运算放大器的
slew rate 即压摆率第一部分
我们将会介绍与压摆率相关的基础理论
并对比压摆率
和放大器电流消耗之间的关系
首先来看什么是压摆率
压摆率被定义为运放输出电压可以达到的
最大摆动速率
它以 V/us 为单位
测量压摆率时可以在运放的输入端
加入一个较大的阶跃信号
比如 1V 幅值
然后测量输出端的电压摆动
即测量输出电平从最终输出量的
10% 增加到 90% 时的时间间隔
有些运放的数据手册中
会专门给出压摆率指标
有些则用大信号的阶跃响应来代替
在这个例子中
我们可以看到
输出电压满幅为 10V
满幅的 10% 和 90% 对应的电平
分别为 1V 和 9V
它们之间的上升时间为 0.25 微秒
从而可以计算出这里的压摆率为 29V/us
压摆率主要描述了
运放在大信号输入时的响应指标
而在正负 100 毫伏以下的小信号
我们应该使用小信号带宽这一指标
二者是不同的
在深入讨论压摆率之前
让我们先来复习一些基础知识
这个等式描述的是流经电容器的电流
等于电容器容值乘以电容器两端电压
随时间的变化率
当电流恒定时
电容器两端电压将会随着时间成线性变化
从而可以表示为v=mt
其中 v(t) 是电压的瞬时值
m 是图中直线的斜率
压摆率是运放的一个很重要的参数
下面我们等效画出运放的输入极和放大极
输入极有个跨导增益 gm
它把运放差分对管输入的电压
转化为本极的输出电流 Iout
Iout 流入放大极
并对放大极的密勒电容
即图中的 Cc 进行充电
根据上一页幻灯片的说明
当 Iout 是常数时
Cc 两端电压将会线性增加
对于缓慢变化的信号 Iout
远小于本极的饱和输出电流 Iout(max)
这说明 Iout 会随着输入差分电压而变化
但对于快速变化的大信号
Iout 将会达到其饱和电流值
在这个例子中
Iout 饱和后运放的输入
将不再是虚短路
即运放的正负输入端引脚间的电压不再相等
因为 Iout 达到饱和成为常数
Cc 两端的电压 Vout
将会随时间以固定斜率线性增加
此时就认为运放达到压摆极限
即其输出转换速度达到了最快
接着上一页幻灯片的说明
这里以三极管输入的运放为例
当我们在输入的差分对管上
施加一个快速变化的大阶跃信号时
有一个三极管将会截止
另一个将会饱和
这时流经饱和三极管的电流
就是上一页幻灯片中提到的 Iout(max)
像前面讨论的一样
Iout(max) 流经 Cc 后
将使 Vout 线性增加
这里我们比较一些运放的压摆率
和静态电流 IQ 之间的关系
比较中采用的参数均是其典型值
在表中的第一行
可见 OPA369 的静态电流非常低
为 0.86uA 其压摆率为五毫伏每微秒
与最后一行静态电流 18.1mA 的 OPA847 相比
OPA369 的压摆率远小于 OPA847 的 850V/us
这说明运放的压摆率越高 带宽越大
其消耗的电流也越大
我们可以用 TINA 来很轻松地仿真压摆率
使用 TINA 里的信号源给运放 OPA2188
输入端加入一个幅值为正负 1 伏的方波信号
在仿真结果中
可以看到在阶跃处输入失调电压
从虚短路时的零伏变化到了 900 毫伏附近
更重要的是输出电压达到了压摆极限
即输出不像输入一样按方波变化
而是在输入阶跃发生处
输出按固定斜率上升 或者下降
逐渐到达正确的输出结果并稳定下来
此时输入端的失调也线性的逐渐减小到零
从仿真可以计算得到
运放 OPA2188 的压摆率为 0.795V/us
十分接近数据手册给出的 0.8V/us
这同时也说明 OPA2188 的 SPICE 模型
在压摆率方面可以准确地模拟真实器件
本页幻灯片着重说明
当运放输出信号以压摆率变化时
运放输出端不再满足虚短路的特性
因为输出变化比输入变化慢
所以输出反馈到输入后
可以在运放正负输入端看到压差
随着输出电压逐渐线性地到达其最终值
输入引脚间的电压逐渐减小
最终运放输入
重新满足虚短路的特性
放大器的数据手册
会提供一个用于描述压摆率和温度关系的曲线图
一般会同时给出正压摆率和负压摆率时的曲线
正压摆率在信号上升时出现
负压摆率在信号下降时出现
一般而言
压摆率的绝对值会随温度的上升而增大
有些运放包括了一个压摆增强电路
从而使器件具有更大的压摆率
这里显示了一个具有压摆增强功能的运放
在大阶跃信号输入时的响应曲线
可以看到这里出现了两段不同的压摆率
初始压摆率很大
而第二阶段的压摆率较小
输出信号逐渐稳定到终值
您或许会好奇
为什么运放不能只有一段很大的压摆率呢
原因在于如果运放只有一段很大的压摆率
输出将在到达终值后出现很大的过冲
或许可以通过某种手段来补偿这种过冲
然而这种补偿
可能会导致反方向变化的信号出现很大过冲
如果这种现象持续下去
将会导致震荡的发生
这一页幻灯片描述了
具有压摆增强功能的运放和普通运放相比的特点
左边是普通运放的响应情况
其中绿色区域显示了小信号输入
或者是差分输入端的输入信号
小于正负 100 毫伏时的情况
可见流入密勒电容的电流 ICc
和输入电压 Vin 成线性关系
蓝色区域显示了大信号输入
或者差分输入端的输入信号
大于正负 100 毫伏时的情况
这时运放达到了其压摆率极限
从而流经米勒电容的电流保持不变
对具有压摆增强功能的运放而言
如右图绿色区域所示
小信号响应与普通运放类似
但当输入差分电压达到
并超过某一特定值以后
如右图的蓝色曲线所示
运放达到了压摆率上限
这时压摆增强功能发挥作用
如图中红色区域所示
因此当给运放输入一个大阶跃信号时
器件将在一开始判断输入电压的大小
如果很大 运放将进入压摆增强模式
使得有足够的电流流入米勒电容
从而提高输出压摆率
当差分输入电压降低时
运放将进入标准压摆模式
而输入电压很小时
运放最后将进行小信号响应
这时输出电压会稳定
运放的输入端也将重新实现虚短路
到目前为止
我们在研究压摆率时只考虑了方波输入的情况
然而对于任何形式的输入信号
压摆率都会限制放大后的结果
或者导致其失真
相关的指标叫做运放的全功率带宽
它描述了最大输出电压和频率的关系
这幅图显示了无压摆率失真时
而在不同频率正弦波输入下
最大输出电压
以 200kHz 处输出信号为例
7.5 伏峰值输出信号
在全功率带宽曲线左下方
从而不会受到压摆率的限制
而十伏峰峰值输出信号
则超出了全功率带宽曲线的范围
将会受到压摆率造成的失真影响
这是对 200kHz 7.5 伏峰值输入的
正弦波压摆率的仿真情况
这个仿真结果验证了对 200kHz 7.5 伏峰值
输出的正弦波压摆率不会使其失真
从结果可以看到
输出很精确地反映了输入信号
此外可以看到图中失调电压 Vos
看起来也是 200kHz 的正弦波
实际上这个失调
可以通过输出电压除以开环带宽 Aol 得到
这个仿真结果
验证了对 200kHz 10V 峰值输出的正弦波
压摆率将使其输出失真
从图中可以看到
与输入的正弦波相比
因为压摆率限制造成的失真影响
输出电压更像是某种三角波
输入失调电压也明显失真
而且不再等于输出电压除以开环带宽 Aol
这一页幻灯片
说明运放的最大输出电压
和信号频率之间可以经由计算进行推导
当无法得到运放的全功率带宽曲线时
您可以试着手工计算
最后的计算公式为 Vp=SR/(2πf)
左边红色框起来的
200kHz 处的计算过程
是对此公式的证明
以上就是本次视频的内容
谢谢观看
请准备好下面的一个小测试
看看你是否已经掌握了本次学习的内容
-
 未学习 1.1 TI 高精度实验室 - 介绍
未学习 1.1 TI 高精度实验室 - 介绍
-
 未学习 1.2 TI 高精度实验室 - 国家仪器虚拟测试仪概述
未学习 1.2 TI 高精度实验室 - 国家仪器虚拟测试仪概述
-
 未学习 2.1 TI 高精度实验室 - 输入失调电压与输入偏置电流
未学习 2.1 TI 高精度实验室 - 输入失调电压与输入偏置电流
-
 未学习 2.2 TI 高精度实验室 - 输入失调电压与输入偏置电流 实验
未学习 2.2 TI 高精度实验室 - 输入失调电压与输入偏置电流 实验
-
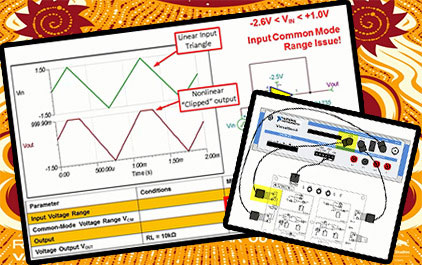 未学习 3.1 TI 高精度实验室 - 输入输出限制
未学习 3.1 TI 高精度实验室 - 输入输出限制
-
 未学习 3.2 输入和输出限制 2
未学习 3.2 输入和输出限制 2
-
 未学习 3.3 输入和输出限制 3
未学习 3.3 输入和输出限制 3
-
 未学习 3.4 TI 高精度实验室 - 输入输出限制 实验
未学习 3.4 TI 高精度实验室 - 输入输出限制 实验
-
 未学习 4.1 功率与温度
未学习 4.1 功率与温度
-
 未学习 5.1 TI 高精度实验室 - 带宽 1
未学习 5.1 TI 高精度实验室 - 带宽 1
-
 未学习 5.2 TI 高精度实验室 - 带宽 2
未学习 5.2 TI 高精度实验室 - 带宽 2
-
 未学习 5.3 TI 高精度实验室 - 带宽 3
未学习 5.3 TI 高精度实验室 - 带宽 3
-
 未学习 5.4 TI 高精度实验室 - 带宽 4
未学习 5.4 TI 高精度实验室 - 带宽 4
-
 未学习 5.5 TI 高精度实验室 - 带宽 实验
未学习 5.5 TI 高精度实验室 - 带宽 实验
-
 未学习 6.1 TI 高精度实验室 - 压摆率 1
未学习 6.1 TI 高精度实验室 - 压摆率 1
-
 未学习 6.2 TI 高精度实验室 - 压摆率 2
未学习 6.2 TI 高精度实验室 - 压摆率 2
-
 未学习 6.3 TI 高精度实验室 - 压摆率 3
未学习 6.3 TI 高精度实验室 - 压摆率 3
-
 未学习 6.4 TI 高精度实验室 - 压摆率 实验
未学习 6.4 TI 高精度实验室 - 压摆率 实验
-
 未学习 7.1 共模抑制
未学习 7.1 共模抑制
-
 未学习 7.2 电源抑制
未学习 7.2 电源抑制
-
 未学习 8.1 TI 高精度实验室 - 噪声 1
未学习 8.1 TI 高精度实验室 - 噪声 1
-
 未学习 8.2 TI 高精度实验室 - 噪声 2
未学习 8.2 TI 高精度实验室 - 噪声 2
-
 未学习 8.3 TI 高精度实验室 - 噪声 3
未学习 8.3 TI 高精度实验室 - 噪声 3
-
 未学习 8.4 TI 高精度实验室 - 噪声 4
未学习 8.4 TI 高精度实验室 - 噪声 4
-
 未学习 8.5 TI 高精度实验室 - 噪声 5
未学习 8.5 TI 高精度实验室 - 噪声 5
-
 未学习 8.6 TI 高精度实验室 - 噪声 6
未学习 8.6 TI 高精度实验室 - 噪声 6
-
 未学习 8.7 TI 高精度实验室 - 噪声 7
未学习 8.7 TI 高精度实验室 - 噪声 7
-
 未学习 8.8 TI 高精度实验室 - 噪声 8
未学习 8.8 TI 高精度实验室 - 噪声 8
-
 未学习 8.9 TI 高精度实验室 - 噪声 实验
未学习 8.9 TI 高精度实验室 - 噪声 实验
-
 未学习 9.1 低失真运算放大器的设计-1
未学习 9.1 低失真运算放大器的设计-1
-
 未学习 9.2 低失真运算放大器的设计-2
未学习 9.2 低失真运算放大器的设计-2
-
 未学习 9.3 低失真运算放大器的设计-3
未学习 9.3 低失真运算放大器的设计-3
-
 未学习 9.4 低失真运算放大器的设计-4
未学习 9.4 低失真运算放大器的设计-4
-
 未学习 10.1 TI 高精度实验室 - 运算放大器:稳定性分析 1
未学习 10.1 TI 高精度实验室 - 运算放大器:稳定性分析 1
-
 未学习 10.2 TI 高精度实验室 - 运算放大器:稳定性分析 2
未学习 10.2 TI 高精度实验室 - 运算放大器:稳定性分析 2
-
 未学习 10.3 TI 高精度实验室 - 运算放大器:稳定性分析 3
未学习 10.3 TI 高精度实验室 - 运算放大器:稳定性分析 3
-
 未学习 10.4 TI 高精度实验室 - 运算放大器:稳定性分析 4
未学习 10.4 TI 高精度实验室 - 运算放大器:稳定性分析 4
-
 未学习 10.5 TI 高精度实验室 - 运算放大器:稳定性分析 5
未学习 10.5 TI 高精度实验室 - 运算放大器:稳定性分析 5
-
 未学习 10.6 TI 高精度实验室 - 运算放大器:稳定性分析 6
未学习 10.6 TI 高精度实验室 - 运算放大器:稳定性分析 6
-
 未学习 10.7 TI 高精度实验室 - 运算放大器:稳定性 - 实验
未学习 10.7 TI 高精度实验室 - 运算放大器:稳定性 - 实验
-
 未学习 11.1 TI 高精度实验室 - 静电释放 (ESD)
未学习 11.1 TI 高精度实验室 - 静电释放 (ESD)
-
 未学习 12.1 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 1
未学习 12.1 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 1
-
 未学习 12.2 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 2
未学习 12.2 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 2
-
 未学习 12.3 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 3
未学习 12.3 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 3
-
 未学习 12.4 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 4
未学习 12.4 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 4
-
 未学习 13.1 电流反馈型运算放大器
未学习 13.1 电流反馈型运算放大器
-
 未学习 13.2 电流反馈运放
未学习 13.2 电流反馈运放
-
 未学习 14.1 如何分析合成器相位噪声
未学习 14.1 如何分析合成器相位噪声
-
 未学习 15.1 全差分放大器 — 差分信号和FDA的介绍
未学习 15.1 全差分放大器 — 差分信号和FDA的介绍
-
 未学习 15.2 全差分放大器 — FDA的输入输出和共模
未学习 15.2 全差分放大器 — FDA的输入输出和共模
-
 未学习 15.3 全差分放大器 — FDA的稳定性和相位裕量
未学习 15.3 全差分放大器 — FDA的稳定性和相位裕量
-
 未学习 15.4 全差分放大器 — FDA的噪声和噪声控制
未学习 15.4 全差分放大器 — FDA的噪声和噪声控制
-
 未学习 15.5 全差分放大器 — 设计用于驱动差分输入ADC的前端电路
未学习 15.5 全差分放大器 — 设计用于驱动差分输入ADC的前端电路
-
 未学习 (中文)3.2 输入和输出限制 2
未学习 (中文)3.2 输入和输出限制 2
-
 未学习 (中文)14.3 电流反馈型运算放大器 Spice 仿真
未学习 (中文)14.3 电流反馈型运算放大器 Spice 仿真
-
 未学习 (中文)15.5 设计用于驱动差分输入ADC的前端电路
未学习 (中文)15.5 设计用于驱动差分输入ADC的前端电路
-
 未学习 运算放大器失真:简介
未学习 运算放大器失真:简介
-
 未学习 (中文)反相输入电容
未学习 (中文)反相输入电容
-
 未学习 (中文)断开差分放大器上的环路
未学习 (中文)断开差分放大器上的环路
-
 未学习 (中文)带宽 - 波特图截止频率
未学习 (中文)带宽 - 波特图截止频率
-
 未学习 (中文)带宽 - 增益和 GBW
未学习 (中文)带宽 - 增益和 GBW
-
 未学习 (中文)带宽 - 同相增益和极点
未学习 (中文)带宽 - 同相增益和极点
-
 未学习 (中文)带宽 - AOL 增益转换率
未学习 (中文)带宽 - AOL 增益转换率
-
 未学习 (中文)带宽 - 实验
未学习 (中文)带宽 - 实验
-
 未学习 (中文)转换率介绍
未学习 (中文)转换率介绍
-
 未学习 (中文)稳定时间
未学习 (中文)稳定时间
-
 未学习 (中文)信号响应
未学习 (中文)信号响应
-
 未学习 (中文)运算放大器失真:简介
未学习 (中文)运算放大器失真:简介
-
 未学习 (中文)输入级
未学习 (中文)输入级
-
 未学习 (中文)光谱密度
未学习 (中文)光谱密度
-
 未学习 (中文)计算 RMS 噪声
未学习 (中文)计算 RMS 噪声
-
 未学习 (中文)计算总噪声
未学习 (中文)计算总噪声
-
 未学习 (中文)简化计算
未学习 (中文)简化计算
-
 未学习 (中文)噪声spice模拟
未学习 (中文)噪声spice模拟
-
 未学习 (中文)验证噪声模型
未学习 (中文)验证噪声模型
-
 未学习 (中文)测量系统噪声
未学习 (中文)测量系统噪声
-
 未学习 (中文)1/F 噪声
未学习 (中文)1/F 噪声
-
 未学习 (中文)噪声 - 实验
未学习 (中文)噪声 - 实验
-
 未学习 理想的无源元件
未学习 理想的无源元件