通用运算放大器
最新课程
- MSPM0G 系列 MCU 时钟配置:在 LED 闪烁的情况下动手操作
- Code Composer Studio™ v20 入门
- 双 DMA 正弦波环回:在 MSPM0G 上实现从 DAC 生成到 ADC 捕捉
- MSPM0G3507 动态 CRC 配置和实时验证
- 视频系列:tiarmclang 编译器
- 汽车应用中的 Jacinto™ 7 处理器
- 可以在 2 分钟内实现无线基础设施应用
- TI 超声成像系统电源方案介绍
- TI 连续血糖监测(CGM)方案介绍
- AI 智能眼镜充电的需求与续航力
热门课程
6.2 TI 高精度实验室 - 压摆率 2
大家好
欢迎来到 TI Precision Labs
德州仪器高精度实验室
本次视频是运算放大器压摆率的第二部分
我们将会探讨体效应对压摆率的影响
还会介绍放大器的建立时间
最后会探讨运放的小信号响应
和大信号响应之间的区别
并简要说明小信号响应的稳定性
体效应(body effect)
是一种常见的影响压摆率的效应
通过改变共模电压
体效应使放大器的压摆率降低
这种影响在同相输入结构的运放电路中尤其明显
因为此时共模电压会随输入电压的变化而变化
对同相放大电路
共模电压越高压摆率越低
一般放大器的压摆率都是在同相电路下测试的
即在最坏条件下测试的
我们将在下一页幻灯片中
解释 IC 内部造成体效应的原因
当然关键是要知道
体效应是影响压摆率的几种重要效应之一
体效应是影响压摆率的几种重要效应之一
在压摆率的视频教程 1 中
我们提到运放的每个输入引脚
都是连接到晶体管的
我们此处假设晶体管为 PMOS
即 P 型 MOSFET
图中所示为典型的 PMOS 横截面
它在 P 型的硅基片上
嵌入了 N 型井作为衬底
在衬底两端各嵌入了 P 型的源极和漏极
从图中可见 在 P 型硅基片
和 N 型衬底之间会形成一个二极管
通常这个二极管是反偏的
当改变芯片工作时的共模电压
即改变二极管 PN 结两端电压时
因为 pn 结耗尽层宽度变化
结电容大小也会发生变化
我们重新回顾一下运放的输入级
来看看体效应电容对压摆率的影响
和前面的视频教程一样
我们在运放输入引脚之间
施加一个大阶跃信号
图中左边的 PMOS 截止
右边 PMOS 导通
从而输入级的所有电流 Iinput
从右边 PMOS 流过造成 Iout 饱和
运放输出达到压摆率上限
然而 一端接地的体效应电容
为 Iout 提供了另一条支路
使得流入密勒电容的电流减小
因为密勒电容两端的电压
和流经电容的电流呈线性关系
所以体效应电容造成的分流
使运放的压摆率降低
在这个例子中
体效应电容和密勒电容都等于 20pF
所以 Iout 是 Iinput 的一半
根据压摆率=Iout/Cc 可知
运放的压摆率也是没有体效应电容时的一半
通过充电
体效应电容两端电压最后会等于共模电压
当运放接成反相放大电路时
如果共模电压保持恒定
输入电压将不会影响压摆率
下面我们来讨论建立时间
运放建立时间被定义如下
从给运放输入端施加一大阶跃信号起
到输出信号进入
并稳定在一定误差带内的时间
这一误差带可以是最终稳定值的
百分比或者是模数转换系统中的最小有效位
因为输入是大阶跃信号
运放输出会受压摆率限制
误差带的范围越窄
比如更小的百分比
会造成建立时间将越长
电容 闭环增益和负载都会影响建立时间
像这幅图一样
许多运放的数据手册
都会给出建立时间和闭环增益的关系
这里仍然要强调
建立时间会随着误差带变窄而延长
建立时间也会随着增益的增大而延长
这是因为运放内部的环路增益
会随运放闭环增益的增加而降低
需要注意的是
运放内部的环路增益和运放的开环增益
运放的闭环增益都是不同的
它被用来校正运放的误差
降低环路增益会使运放的建立时间延长
我们可以使用 TINA-TI 里的瞬态分析功能
很方便的仿真运放的建立时间
为了保证仿真结果
我们要尽量使仿真条件
和数据手册上的测试条件一样
比如输入阶跃大小
外围电路 负载电容等
在这里 我们对 OPA827 的建立时间进行仿真
条件如下 反相放大 闭环增益为 1
输入 10V 阶跃信号 100pF 负载电容
图中显示了 OPA827 建立时间的瞬态分析结果
建立时间包含了两部分
一是输出电压的摆动时间
二是进入并稳定在误差范围内的时间
输出电压稳定在误差范围内的细节
在此图中无法观察
我们将对其进行放大
并在后面几张幻灯片中进行分析
在放大观察建立时间之前
我们先来设置最终要求的误差允许范围
这样会更易于观察和分析
通过点击 TINA 中的 Post-processor 图标
我们在 Vout 上方和下方添加两条水平基准线
作为误差允许范围
它们到 Vout 的终值相距 0.01%
因为 Vout 的最终值为 10V
所以这里误差允许范围是 0.999V 到 10.001V
通过对结果的放大观察
我们可以看到
在稳定过程中
会有一些过冲和阻尼震荡的发生
在这里
我们看到在经历了一次过冲和一次振铃后
输出稳定在误差范围内
整个建立时间约为 400ns
对比数据手册中给出的 550ns 建立时间
此处我们的仿真结果是可以接受的
到目前为止
我们在讨论压摆率时
一直使用了大信号输入
通常输入信号的幅值大于等于 1V
下面我们来看看
当给运放输入一个幅值
小于等于 100mV 的小阶跃信号时
运放会怎么响应
与前面讲到的大信号输入不同的是
后面几页幻灯片讨论的小信号输入
通常不会使运放达到其压摆率极限
通常不会使运放达到其压摆率极限
我们同样可以使用 TINA 来仿真
小信号输入时运放的上升时间
这里是对 OPA827
输入一个 100mV 小阶跃信号时的仿真结果
下一页幻灯片
我们将会放大上升沿
来精确测量小信号输入的上升时间
这里对仿真结果放大观察
为了和压摆率进行对比
我们在计算小阶跃信号输入的上升时间时
仍沿用 V/us 作为单位
通过测量最终稳定值的 10%到 90%之间的时间
我们可以得到上升时间为 11.7V/us
这和数据手册上给出的
28V/us 的压摆率相比似乎相差很多
这是因为我们输入的信号
没有使运放达到压摆率的上限
所以这里的上升时间和压摆率指标是不同的
是什么造成了这种时间的差异呢
您可能还记得
我们在压摆率的第一个视频中提到
一个大阶跃信号可能会让运放达到压摆率极限
从而使运放无法线性工作
但小信号则可以保证运放工作在线性区
上升时间仅仅由运放的带宽所限制
我们可以通过简单的计算来进行证明
首先 我们定义运放的上升时间
为运放输出信号
从其稳定输出值的 10%到 90% 之间的时间差
其次 我们假设运放的输出只接一个电容
即电路为一阶电路
从而可以求出运放输出电压 Vout 的表达式
因为我们最终要解出上升时间
所以我们分别令 Vout
等于 10%的运放稳定输出值
和 90%的运放稳定输出值
从而得到这两个时间点的表达式
将它们相减 就可以求出上升时间了
这里得到的上升时间是 tr=2.19τ
接着前面的推导
我们引入放大器闭环截止带宽 fc
它等于 1/(2*pi*RC)
而 τc=RC
我们带入上升时间 tr 和 τc 的关系式
即 tr=2.19τ
得到上升时间和闭环带宽之间的表达式
tr=0.35/fc
下面我们用仿真来验证前面的推导
OPA2188 的数据手册上
给出其增益带宽积为 2MHz
代入我们上一页幻灯片得到的
tr=0.35/fc
可知上升时间为 175ns
这里仿真得到的上升时间为 138ns
和计算结果之间存在 20%的误差
但作为一种近似这个结果是不错的
因为实际运放并不简单是一阶系统
而且仿真模型和实际器件
在综合准确度上也是有差异的
有意思的是
在前面的小信号上升时间表达式中
放大器带宽是式中唯一的变量
这说明上升时间与小信号的阶跃幅值无关
当然阶跃幅值不能超过 100mV
否则输入就不是小信号了
通过仿真可以来验证上升时间
是否和阶跃幅值无关
我们给运放分别输入 10mV 到 100mV 之间
不同幅值的阶跃信号
可以看到仿真得到的上升时间都是一样的
但是对于大输入信号而言
上升时间和输入信号的幅值是相关的
这正是因为压摆率
限制了运放输出电压的改变速度
使它最大只能以固定的斜率上升
这里显示的是当压摆率为 0.8V/us 时
上升时间随输入阶跃幅值的增大而延长
运放小信号的阶跃响应
也可以被用来判断系统的稳定性
一般而言 对任何一个像运放这样的
二阶或者三阶系统
都可以通过在输入端施加方波
并测试输出端波形来判断系统的稳定性
鉴于大信号会受压摆率的限制而造成非线性失真
为了保证测试时运放工作于线性放大状态
应该使用小信号输入
一般而言
响应的输出过冲越大
运放就越不稳定
这个 OPA827 的例子中
为保证稳定
负载电容的最大值是 1000pF
这时的输出过冲为 60%
这一页幻灯片从二阶系统复频域
和时域表达式上简单说明过冲和稳定性的关系
从右图可以看到
通过改变阻尼系数 zeta 的值
会改变系统的过冲量
稳定性将会在其他视频教程中详述
这里我们不再深入讨论
以上就是本次视频的内容
谢谢观看
请准备好下面的一个小测试
看看您是否掌握了本次学习的内容
-
 未学习 1.1 TI 高精度实验室 - 介绍
未学习 1.1 TI 高精度实验室 - 介绍
-
 未学习 1.2 TI 高精度实验室 - 国家仪器虚拟测试仪概述
未学习 1.2 TI 高精度实验室 - 国家仪器虚拟测试仪概述
-
 未学习 2.1 TI 高精度实验室 - 输入失调电压与输入偏置电流
未学习 2.1 TI 高精度实验室 - 输入失调电压与输入偏置电流
-
 未学习 2.2 TI 高精度实验室 - 输入失调电压与输入偏置电流 实验
未学习 2.2 TI 高精度实验室 - 输入失调电压与输入偏置电流 实验
-
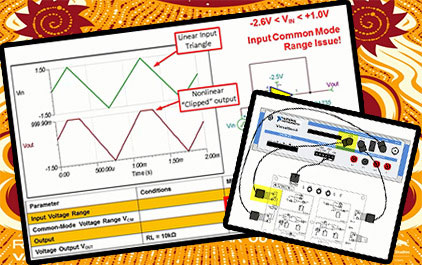 未学习 3.1 TI 高精度实验室 - 输入输出限制
未学习 3.1 TI 高精度实验室 - 输入输出限制
-
 未学习 3.2 输入和输出限制 2
未学习 3.2 输入和输出限制 2
-
 未学习 3.3 输入和输出限制 3
未学习 3.3 输入和输出限制 3
-
 未学习 3.4 TI 高精度实验室 - 输入输出限制 实验
未学习 3.4 TI 高精度实验室 - 输入输出限制 实验
-
 未学习 4.1 功率与温度
未学习 4.1 功率与温度
-
 未学习 5.1 TI 高精度实验室 - 带宽 1
未学习 5.1 TI 高精度实验室 - 带宽 1
-
 未学习 5.2 TI 高精度实验室 - 带宽 2
未学习 5.2 TI 高精度实验室 - 带宽 2
-
 未学习 5.3 TI 高精度实验室 - 带宽 3
未学习 5.3 TI 高精度实验室 - 带宽 3
-
 未学习 5.4 TI 高精度实验室 - 带宽 4
未学习 5.4 TI 高精度实验室 - 带宽 4
-
 未学习 5.5 TI 高精度实验室 - 带宽 实验
未学习 5.5 TI 高精度实验室 - 带宽 实验
-
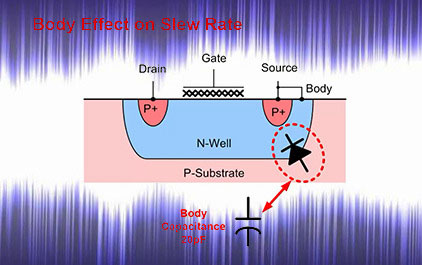 未学习 6.1 TI 高精度实验室 - 压摆率 1
未学习 6.1 TI 高精度实验室 - 压摆率 1
-
 未学习 6.2 TI 高精度实验室 - 压摆率 2
未学习 6.2 TI 高精度实验室 - 压摆率 2
-
 未学习 6.3 TI 高精度实验室 - 压摆率 3
未学习 6.3 TI 高精度实验室 - 压摆率 3
-
 未学习 6.4 TI 高精度实验室 - 压摆率 实验
未学习 6.4 TI 高精度实验室 - 压摆率 实验
-
 未学习 7.1 共模抑制
未学习 7.1 共模抑制
-
 未学习 7.2 电源抑制
未学习 7.2 电源抑制
-
 未学习 8.1 TI 高精度实验室 - 噪声 1
未学习 8.1 TI 高精度实验室 - 噪声 1
-
 未学习 8.2 TI 高精度实验室 - 噪声 2
未学习 8.2 TI 高精度实验室 - 噪声 2
-
 未学习 8.3 TI 高精度实验室 - 噪声 3
未学习 8.3 TI 高精度实验室 - 噪声 3
-
 未学习 8.4 TI 高精度实验室 - 噪声 4
未学习 8.4 TI 高精度实验室 - 噪声 4
-
 未学习 8.5 TI 高精度实验室 - 噪声 5
未学习 8.5 TI 高精度实验室 - 噪声 5
-
 未学习 8.6 TI 高精度实验室 - 噪声 6
未学习 8.6 TI 高精度实验室 - 噪声 6
-
 未学习 8.7 TI 高精度实验室 - 噪声 7
未学习 8.7 TI 高精度实验室 - 噪声 7
-
 未学习 8.8 TI 高精度实验室 - 噪声 8
未学习 8.8 TI 高精度实验室 - 噪声 8
-
 未学习 8.9 TI 高精度实验室 - 噪声 实验
未学习 8.9 TI 高精度实验室 - 噪声 实验
-
 未学习 9.1 低失真运算放大器的设计-1
未学习 9.1 低失真运算放大器的设计-1
-
 未学习 9.2 低失真运算放大器的设计-2
未学习 9.2 低失真运算放大器的设计-2
-
 未学习 9.3 低失真运算放大器的设计-3
未学习 9.3 低失真运算放大器的设计-3
-
 未学习 9.4 低失真运算放大器的设计-4
未学习 9.4 低失真运算放大器的设计-4
-
 未学习 10.1 TI 高精度实验室 - 运算放大器:稳定性分析 1
未学习 10.1 TI 高精度实验室 - 运算放大器:稳定性分析 1
-
 未学习 10.2 TI 高精度实验室 - 运算放大器:稳定性分析 2
未学习 10.2 TI 高精度实验室 - 运算放大器:稳定性分析 2
-
 未学习 10.3 TI 高精度实验室 - 运算放大器:稳定性分析 3
未学习 10.3 TI 高精度实验室 - 运算放大器:稳定性分析 3
-
 未学习 10.4 TI 高精度实验室 - 运算放大器:稳定性分析 4
未学习 10.4 TI 高精度实验室 - 运算放大器:稳定性分析 4
-
 未学习 10.5 TI 高精度实验室 - 运算放大器:稳定性分析 5
未学习 10.5 TI 高精度实验室 - 运算放大器:稳定性分析 5
-
 未学习 10.6 TI 高精度实验室 - 运算放大器:稳定性分析 6
未学习 10.6 TI 高精度实验室 - 运算放大器:稳定性分析 6
-
 未学习 10.7 TI 高精度实验室 - 运算放大器:稳定性 - 实验
未学习 10.7 TI 高精度实验室 - 运算放大器:稳定性 - 实验
-
 未学习 11.1 TI 高精度实验室 - 静电释放 (ESD)
未学习 11.1 TI 高精度实验室 - 静电释放 (ESD)
-
 未学习 12.1 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 1
未学习 12.1 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 1
-
 未学习 12.2 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 2
未学习 12.2 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 2
-
 未学习 12.3 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 3
未学习 12.3 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 3
-
 未学习 12.4 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 4
未学习 12.4 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 4
-
 未学习 13.1 电流反馈型运算放大器
未学习 13.1 电流反馈型运算放大器
-
 未学习 13.2 电流反馈运放
未学习 13.2 电流反馈运放
-
 未学习 14.1 如何分析合成器相位噪声
未学习 14.1 如何分析合成器相位噪声
-
 未学习 15.1 全差分放大器 — 差分信号和FDA的介绍
未学习 15.1 全差分放大器 — 差分信号和FDA的介绍
-
 未学习 15.2 全差分放大器 — FDA的输入输出和共模
未学习 15.2 全差分放大器 — FDA的输入输出和共模
-
 未学习 15.3 全差分放大器 — FDA的稳定性和相位裕量
未学习 15.3 全差分放大器 — FDA的稳定性和相位裕量
-
 未学习 15.4 全差分放大器 — FDA的噪声和噪声控制
未学习 15.4 全差分放大器 — FDA的噪声和噪声控制
-
 未学习 15.5 全差分放大器 — 设计用于驱动差分输入ADC的前端电路
未学习 15.5 全差分放大器 — 设计用于驱动差分输入ADC的前端电路
-
 未学习 (中文)3.2 输入和输出限制 2
未学习 (中文)3.2 输入和输出限制 2
-
 未学习 (中文)14.3 电流反馈型运算放大器 Spice 仿真
未学习 (中文)14.3 电流反馈型运算放大器 Spice 仿真
-
 未学习 (中文)15.5 设计用于驱动差分输入ADC的前端电路
未学习 (中文)15.5 设计用于驱动差分输入ADC的前端电路
-
 未学习 运算放大器失真:简介
未学习 运算放大器失真:简介
-
 未学习 (中文)反相输入电容
未学习 (中文)反相输入电容
-
 未学习 (中文)断开差分放大器上的环路
未学习 (中文)断开差分放大器上的环路
-
 未学习 (中文)带宽 - 波特图截止频率
未学习 (中文)带宽 - 波特图截止频率
-
 未学习 (中文)带宽 - 增益和 GBW
未学习 (中文)带宽 - 增益和 GBW
-
 未学习 (中文)带宽 - 同相增益和极点
未学习 (中文)带宽 - 同相增益和极点
-
 未学习 (中文)带宽 - AOL 增益转换率
未学习 (中文)带宽 - AOL 增益转换率
-
 未学习 (中文)带宽 - 实验
未学习 (中文)带宽 - 实验
-
 未学习 (中文)转换率介绍
未学习 (中文)转换率介绍
-
 未学习 (中文)稳定时间
未学习 (中文)稳定时间
-
 未学习 (中文)信号响应
未学习 (中文)信号响应
-
 未学习 (中文)运算放大器失真:简介
未学习 (中文)运算放大器失真:简介
-
 未学习 (中文)输入级
未学习 (中文)输入级
-
 未学习 (中文)光谱密度
未学习 (中文)光谱密度
-
 未学习 (中文)计算 RMS 噪声
未学习 (中文)计算 RMS 噪声
-
 未学习 (中文)计算总噪声
未学习 (中文)计算总噪声
-
 未学习 (中文)简化计算
未学习 (中文)简化计算
-
 未学习 (中文)噪声spice模拟
未学习 (中文)噪声spice模拟
-
 未学习 (中文)验证噪声模型
未学习 (中文)验证噪声模型
-
 未学习 (中文)测量系统噪声
未学习 (中文)测量系统噪声
-
 未学习 (中文)1/F 噪声
未学习 (中文)1/F 噪声
-
 未学习 (中文)噪声 - 实验
未学习 (中文)噪声 - 实验
-
 未学习 理想的无源元件
未学习 理想的无源元件