人工智能
最新课程
- LP-MSPM0G3507 按键输入基础:基于计时器的短按检测
- MSPM0G 系列 MCU 时钟配置:在 LED 闪烁的情况下动手操作
- Code Composer Studio™ v20 入门
- 双 DMA 正弦波环回:在 MSPM0G 上实现从 DAC 生成到 ADC 捕捉
- MSPM0G3507 动态 CRC 配置和实时验证
- 视频系列:tiarmclang 编译器
- 汽车应用中的 Jacinto™ 7 处理器
- 可以在 2 分钟内实现无线基础设施应用
- TI 超声成像系统电源方案介绍
- TI 连续血糖监测(CGM)方案介绍
热门课程
TI-RSLK 模块 17 - 讲座视频 - 控制系统
大家好,我是
在本模块中,我们将讨论控制系统。
现在,在整个课程中,
我们一直在努力解决机器人的问题。
有各种不同的问题,
需要我们去解决,
但这些问题全部涉及到一件事
让机器人按照要求执行一些任务。
因此,在本模块中,
我们将讨论闭环。
换句话说,我们将讨论的
输入将是线传感器、
距离传感器或码盘。
这些传感器使得机器人可以感知外界
正在发生的情况,然后在本模块中建立
一组方程,这些方程允许我们使用该输入
设置两个电机的
按照您的要求运行。
这就是我要表达的意思,我们将控制该机器人。
我们将使它听从我们的指挥。
这将是本模块的目标。
现在,控制系统无处不在,
许多应用中都有它们的身影。
许多嵌入式系统实际上在内部
都有一个控制系统,无论是在汽车中,
在洗衣机等电器中,在工业机器人等工业
设备中,还是在医疗设备中,都是如此。
存在大量符合我们将在本模块中看到的
理论的应用,它们用于影响和控制
我们的世界。
我说过,本模块中系统将闭环。
因此,举例来说,如果我尝试使电机
以恒定的速度旋转,
我将使用码盘,
该码盘就是我们要使用的传感器。
该传感器的输出显然将是速度。
我将创建一组控制方程,
也就是将编写一段软件代码,
用于确定驱动两个电机的适当
按照我的要求运行。
很显然,本例中的物理设备是电机
这是我的
那么,这个控制系统
由一个环路组成,这些组件在环路中相互
连接在一起。
正如我说过的,目标是让电机
以恒定的速度转动。
这将是我们的目标。
那么,让我向您展示这是怎么发生的。
在接下来的几张幻灯片中,
将显示大量的数学公式。
平心而论,您实际上不必了解所有这些
数学公式就可以完成本课程
和配套的实验。
但是,可以这么说,如果您以后会选修控制系统
课程,或者您过去已经
参加了该课程,那么我想这时
在这里做这个实验将帮助您了解和领悟
您将在课程中看到的理论。
换句话说,控制系统可能需要整整一门课程或
一系列课程进行讲授。
在这里,在这个简短的视频中,在这一个模块中,
我们当然不会看到全部内容。
但是,可以这么说,您将看到一个控制系统
的所有组件。
因此,再说一次,我们将实现所需的速度。
比如说我想以
然后,我们将使用一个码盘
测量电机的速度。
这称为状态评估器。
那么,在这里,我们有当前速度。
我们将计算误差,
它是目标值与估算值之间的差异。
那么,本实验模块的
目的是建立一个控制方程,
或控制器,它采用测量值作为输入,
确定新的
以使得实际测量速度和某个目标速度相等。
好的,让我向您展示这是怎么发生的。
好,在我们开始之前,
让我们讨论一下它的效果如何,
以便我们可以讨论控制系统的一些性能指标。
换句话说,如果我试着让转速达到
让我查看下实际速度,
我现在可以看到稳定状态下的
平均误差。
换句话说,x*
平均差值是多少。
这是一个精度指标,
即目标值与实际值之间的平均差异。
我们在上一个视频中提到了时间常数。
在上一个视频中,我们所做的是,
我们将占空比从
现在,让我们执行一些不同的操作。
让我们更改目标速度。
那么如果我将目标速度从
现在问题来了,它的响应速度有多快。
控制系统对输入变化的响应
控制系统对输入变化的响应
由底部的三条曲线表示。
换句话说,我将更改工作点。
如果我更改小车上的摩擦力或负载,
也有可能发生上述情况。
现在,如果把速度看作时间的函数,会发生什么呢?
我们期望的结果
是精密、平滑并且速度很快。
我们将再次使用时间常数的概念,
时间常数是在我更改
工作点之后达到最终速度的
所需的时间。
因此,现在它将是系统的时间常数,而不仅是
电机的时间常数。
但可能发生两件糟糕的事情
它可能会发生过阻尼,也可能发生欠阻尼。
欠阻尼意味着它具有大量的振荡。
实际上,振荡可能多到
系统变得不稳定。
这会是一件糟糕的事情。
另一件事
它可能非常慢,这也很糟糕。
那么,我们想做的是,研究我们控制系统
的响应速度,
电机、码盘、软件、PWM、H
整个环路,研究它的
响应速度有多快。
这称为系统的时间常数。
好,我们在上一个模块中也向您
展示了该幻灯片。
再说一次,实际情况可能会与理论有所差别,
如果我们尝试实践控制系统理论,
那么我们希望将电机的响应
以微分方程形式表示。
这是一个非常简单的线性模型,
用于描述电机的行为。
如果您查看电机的占空比输入
和速度输出,
在时域或频域中进行查看,
您可以尝试编写一个方程来对这现象进行描述。
电机实际上不是线性的,
摩擦力是一个大问题。
我们实际上不需要该理论即可
成功实现和解决该实验。
但是,可以这么说,许多人
花费整个职业生涯尝试建立
一种精确的模型来描述物理世界的行为。
这里是一个电机特性的示例图,
这是一个电机,
我要关注的是
计算电机实际所消耗的功率
它由占空比进行控制
该功率是速度的函数。
那么,我增大功率,
但电机完全没有旋转。
这称为保持摩擦力。
因此,电机中存在一种摩擦力,
如果您只为电机提供很小的功率,它完全不会旋转。
但是,接下来,它会突然开始旋转。
我们可以从中注意到的另一个现象是,
这组电机具有很好的线性。
因此,随着我增大功率,速度将以
几乎同样的方式增大。
但您将看到,这里有七个不同的电机,
它们彼此之间差别很大。
那么该幻灯片的目的是演示两点。
首先,电机完全不遵循该方程。
它们不是线性的,我们无法为它编写一个微分方程,
此外还有这样一个事实:在这里,摩擦力是我们的敌人,
而我们很难对该摩擦力本身的
影响进行建模。
因此,我们将需要根据经验进行一些调整。
我们将在下一张幻灯片中对此进行讨论。
再说一次,这里是实验所用的理论,
但您不必了解它即可进行实验。
但是,如果您参加控制系统课程,您将看到该理论。
该理论指出,如果我们
在时域中看到一个反馈电路,
我们实际上可以在频域中表示它。
因此,当您看到作为
它是拉普拉斯
但是,这个理论其实给了我们一些提示,
关于我们可能希望尝试的三类控制参数。
关于我们可能希望尝试的三类控制参数。
第一类是,输出与误差成
线性比例关系。
第二类是,输出与误差成
积分关系。
第三类是微分关系。
因此我们有比例项、积分项
和微分项。
现在,事实证明,我们的传感器具有
如此大的噪声,以至于我们根本不会在本课程中尝试
执行微分信号。
请不要尝试它。
因为您的传感器噪声实在太大。
那么,让我们讨论一下什么是有用的。
这是经验之谈。
我们来这样想
我们要尝试控制电机的速度,
就在这里。
让我们再次暂且假设
我们将尝试将转速提高至
您应该记得,这里是我们的目标状态,x*。
您测量了速度,x,或
即估算速度。
现在,您要做什么?
嗯,我说的是,如果误差
如果您的误差是
-1、0、1、2
换句话说,如果我以
这对我而言已经足够接近了。
那么,我将使电机保持不动。
另一方面,如果电机旋转得过快,
如果旋转速度是
我要做的是减小占空比。
这里是占空比,正如您知道的,
它的值将介于
它的值将介于
它的值将介于
它的值将介于
这就是我们的占空比。
因此,如果电机旋转得过快,我将减小
如果旋转得过慢,我将增大它。
这其实和我们
开汽车时候是类似的。
我们只是上下调节汽车中的油门,
直到我们的眼睛看到
汽车以正确速度行驶。
这称为渐进式控制。
对于控制系统而言,它非常慢,但它非常稳定。
只要您的方向正确,只要您在行驶得
过快时减小功率,在行驶得过慢时
增大功率,
系统就不会变得不稳定。
因此,尽管比较慢,但这是一个很好的开始。
那么,让我们来讨论使它更快的方法。
我们将讨论比例和积分。
我已经告诉过您,我们不会使用微分。
这里向我们展示的是,
我如何将比例、积分
和微分的理论定义
映射到实际执行的软件上,
让软件在控制器上以固定速率执行?
那么,我们将从这个概念开始,
就像我们的
我们将以恒定时间间隔来运行我们的控制器。
例如,每
我的控制器。
这将是一个优先级相当高的周期性中断。
如果我运行一个比例控制器,
我会计算误差,然后使占空比
成为误差的线性函数。
我们稍后会看到一个相关的示例。
如果我想创建一个积分控制器,
那么我基本上会采用积分方程。
事实上这不再是一个
连续变量,它将成为一个离散时间。
因此,它会把它自身
从一个非连续间隔转换为一个离散和。
然后,我将对它进行优化。
我不是每次都把它累加起来,
而是仅把这里的当前值添加到前一个值。
这将在本质上是一个离散
间隔。
我可以对离散微分执行同样的操作。
如果您自己有一个很好的传感器,
那么您可以添加一个微分项。
但是,再说一遍,不要在本课程中这么做。
您的传感器没有这么好。
然后我可以对它们进行组合,
我可以只使用比例项,或只使用积分项,
我可以同时使用比例项和积分项,
也可以同时使用比例项微分项,
或者可以同时使用所有这些项。
因此,在我学会运用这些方程之后,
我希望能够用任何我想要的方式
组合它们。
请记住,我们将以大约比电机快
速度运行它。
它的另一个问题是,传感器也具有
速度。
因此我们必须了解我们的
传感器有多快,以便我们不会使控制器的
运行速度快于我们的传感器。
因此,将存在一个最佳位置,
使控制器的运行速度慢于传感器,
但快于电机。
您将看到有时我们需要某个
是非整数值的数。
因此,如果我们需要使用这样的数,
那么基本来说,我要做的是,
把看起来像是浮点数的值
用整数的运算结果来表示。
因此,我实际上可以将任何数字近似表示为
为两个整数的商。
因此,我们不必在我们的系统上
实际进行浮点运算。
如果我们不使用浮点运算,
这将极大地加快我们的控制器。
因此,我们将使用定点运算。
每当您需要某个值的小数部分时,
我们可以把它分离出来。
这里的技巧是,我们必须先执行乘法,然后再执行除法。
因此,您会注意到,我先执行乘法,然后再执行除法。
好,让我们来演示几个示例。
那么,这是一个比例控制器。
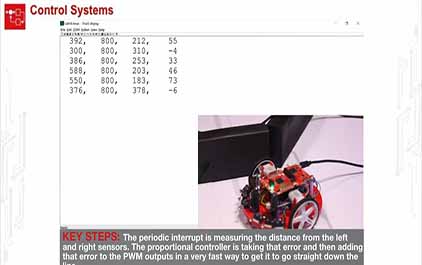
我所做的是,我用红外线传感器,就在那里,
用于测量距离。
我对它进行了校准,因此距离
机器人的中心到墙的距离。
我在这里的目标是把该距离控制到
250
就是这个距离,从这里到那里。
那么,就像我在其他示例中所做的那样,
我将计算误差,也就是目标值和
估算值之间的差异。
我使用
来估算该距离。
现在,我将使用比例关系
并且将计算占空比。
我将把占空比表示为
误差的线性或比例的形式。
在本例中,我添加了一个偏移量。
因此,如果误差等于
那么我将让两个电机都以大约
我将让两个电机都以大约
如果误差是
但是,如果我的误差为正,那么我将减小
让左轮的占空比较小,
而右轮占空比较大,从而对它进行调节。
如果我的误差为负,那么方向将相反。
我将限制占空比,以便它不会出现异常行为。
然后以快于电机的速度运行它。
这是我实际上实现的效果,
它运行得很好,
机器人很好地沿墙行进。
如果您愿意,您可以沿着左侧的墙行进,
也可以沿着中间行进。
这个比例控制器可以起到很好的效果,
如果您想使用距离传感器让机器人沿直线前进。
如果您想使用距离传感器让机器人沿直线前进。
让我们看看另一个示例,让我们看看积分控制器。
那么,我将再次计算误差,
然后调节占空比。
我将向上或向下调节占空比,具体取决于
我的误差有多大。
换句话说,如果我行进得很慢,
我将大幅增大占空比。
如果我行进得很快,我将大幅减小占空比。
我还是会将占空比限制在
一个合理的区间之内,
并以固定的速率运行控制器。
在这里,我的策略是,必须保证方向正确。
换话句话说,如果您想行进得更快,
就使占空比增大。
如果您想行进得更慢,就使占空比减小。
如果您向右行进得太多,就向左转。
如果您向左行进得太多,就向右转。
因此,保证控制器的方向正确,
然后您可以做的是,调整或调节参数,
从而使机器人按照您的要求运行。
因此,如果您的系统发生过阻尼
它响应很慢
那么您可以增大增益。
如果您的系统发生过阻尼
我是说欠阻尼(口误),
如果它发生过阻尼,很慢,
就增大增益。
如果它发生欠阻尼,就减小增益。
该策略可以起到很好的效果。
您应该记得,积分控制器的目的
是调节您增加的幅度,
它是误差的函数。
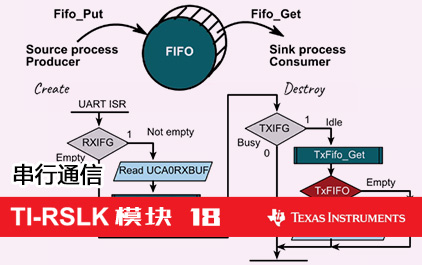
我在这里针对本次实验有几点建议。
那就是,不要忘记其他实验,
不要相信您的传感器,它们有误差。
使用一些调试技巧,
你可以将传感器读取的内容或测量值可视化,
把调试结果存储到
或者通过串口传到电脑,或者使用
您需要使测量值可视化,
因为如果您的控制器无法看到墙,
它就无法沿墙行进。
您还需要使控制器的每个阶段可视化,
换句话说,如果您的控制器有多个步骤
如果这样,那么那样,如果这样,那么那样
您需要确保您可以看到机器人在想什么,
因为当它撞到墙时,
您会说,当它撞到墙时它在
想什么呢?
要知道原因您只需要问,
您必须能够看到它当时在想什么。
好,控制器通常具有多个参数,
我建议您一次改变一个旋钮。
您应该意识到,稳定地沿着赛道前进
要比走得快更重要。
因此我鼓励您从稳定性开始,
确保您的控制器是稳定的。
然后您可以对它进行调节,使它具有更高的响应速度。
希望您喜欢本次实验,下面我们即将开始终极挑战。
-
 未学习 TI-RSLK 模块 1 - 讲座视频 – 使用 CCS 在 LaunchPad 上运行代码
未学习 TI-RSLK 模块 1 - 讲座视频 – 使用 CCS 在 LaunchPad 上运行代码
-
 未学习 TI-RSLK 模块 1 - 实验视频 1.1 – 安装 tirslk_maze
未学习 TI-RSLK 模块 1 - 实验视频 1.1 – 安装 tirslk_maze
-
 未学习 TI-RSLK 模块 1 - 实验视频 1.2 – 安装 CCS 和调试
未学习 TI-RSLK 模块 1 - 实验视频 1.2 – 安装 CCS 和调试
-
 未学习 TI-RSLK 模块 1 - 实验视频 1.3 – 运行 TExaS 逻辑分析仪
未学习 TI-RSLK 模块 1 - 实验视频 1.3 – 运行 TExaS 逻辑分析仪
-
 未学习 TI-RSLK 模块 1 - 实验视频 1.4 – 运行 TExaS 示波器
未学习 TI-RSLK 模块 1 - 实验视频 1.4 – 运行 TExaS 示波器
-
 未学习 TI-RSLK 模块 2 - 讲座视频 – 电压、电流和功率
未学习 TI-RSLK 模块 2 - 讲座视频 – 电压、电流和功率
-
 未学习 TI-RSLK 模块 2 - 实验视频 2.1 – 测量电容器的阻抗
未学习 TI-RSLK 模块 2 - 实验视频 2.1 – 测量电容器的阻抗
-
 未学习 TI-RSLK 模块 2 - 实验视频 2.2 – LED (I,V) 响应曲线、指数关系
未学习 TI-RSLK 模块 2 - 实验视频 2.2 – LED (I,V) 响应曲线、指数关系
-
 未学习 TI-RSLK 模块 3 - 讲座视频 - ARM Cortex M 架构
未学习 TI-RSLK 模块 3 - 讲座视频 - ARM Cortex M 架构
-
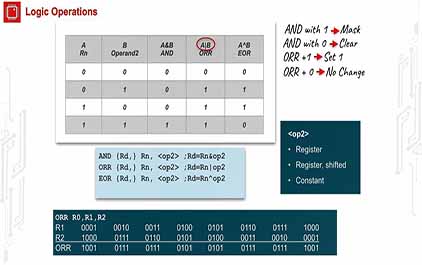 未学习 TI-RSLK 模块 3 - 讲座视频 - ARM Cortex M 组件
未学习 TI-RSLK 模块 3 - 讲座视频 - ARM Cortex M 组件
-
 未学习 TI-RSLK 模块 3 - 实验视频 3.1 - 调试解决方案、可视化、断点和单步执行
未学习 TI-RSLK 模块 3 - 实验视频 3.1 - 调试解决方案、可视化、断点和单步执行
-
 未学习 TI-RSLK 模块 4 - 讲座视频 - C 语言编程
未学习 TI-RSLK 模块 4 - 讲座视频 - C 语言编程
-
 未学习 TI-RSLK 模块 4 - 讲座视频 - 设计
未学习 TI-RSLK 模块 4 - 讲座视频 - 设计
-
 未学习 TI-RSLK 模块 4 - 讲座视频 - 调试
未学习 TI-RSLK 模块 4 - 讲座视频 - 调试
-
 未学习 TI-RSLK 模块 4 - 实验视频 4.1 - 调试解决方案、可视化、变量、单步执行
未学习 TI-RSLK 模块 4 - 实验视频 4.1 - 调试解决方案、可视化、变量、单步执行
-
 未学习 TI-RSLK 模块 4 - 实验视频 4.2 - 调试解决方案、可视化、断点、单步执行
未学习 TI-RSLK 模块 4 - 实验视频 4.2 - 调试解决方案、可视化、断点、单步执行
-
 未学习 TI-RSLK 模块 5 - 讲座视频 - 电池和电压
未学习 TI-RSLK 模块 5 - 讲座视频 - 电池和电压
-
 未学习 TI-RSLK 模块 5 - 实验视频 5.1 - 测量电池的电压和电流
未学习 TI-RSLK 模块 5 - 实验视频 5.1 - 测量电池的电压和电流
-
 未学习 TI-RSLK 模块 5 - 实验视频 5.2 - 连接电机驱动器和配电板
未学习 TI-RSLK 模块 5 - 实验视频 5.2 - 连接电机驱动器和配电板
-
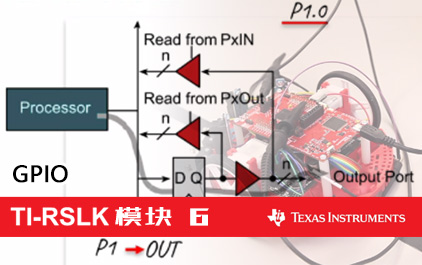 未学习 TI-RSLK 模块 6 - 讲座视频 - GPIO MSP432
未学习 TI-RSLK 模块 6 - 讲座视频 - GPIO MSP432
-
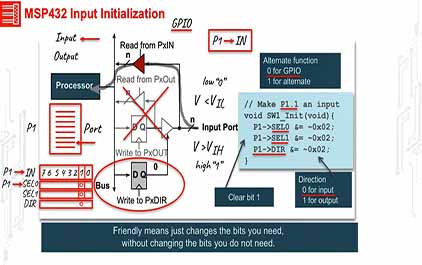 未学习 TI-RSLK 模块 6 - 讲座视频 - GPIO 编程
未学习 TI-RSLK 模块 6 - 讲座视频 - GPIO 编程
-
 未学习 TI-RSLK 模块 6 - 实验视频 6.1 - 演示反射传感器的工作原理
未学习 TI-RSLK 模块 6 - 实验视频 6.1 - 演示反射传感器的工作原理
-
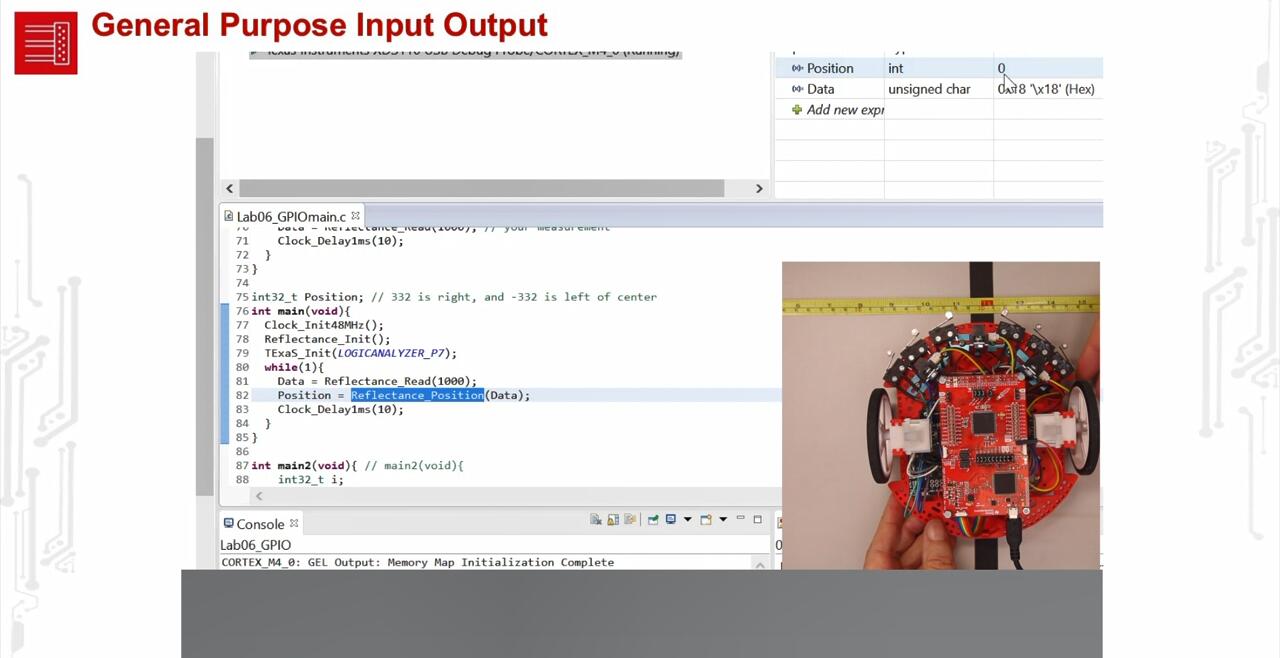 未学习 TI-RSLK 模块 6 - 实验视频 6.2 - 演示实验解决方案 - 测试线路传感器
未学习 TI-RSLK 模块 6 - 实验视频 6.2 - 演示实验解决方案 - 测试线路传感器
-
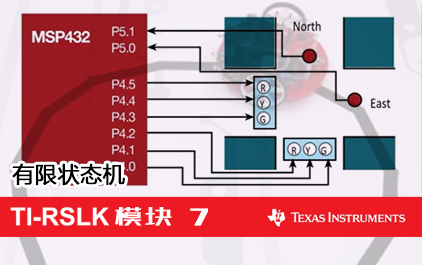 未学习 TI-RSLK 模块 7 - 讲座视频 - 有限状态机理论
未学习 TI-RSLK 模块 7 - 讲座视频 - 有限状态机理论
-
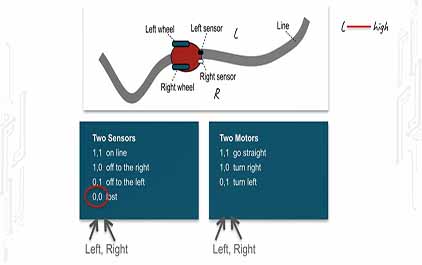 未学习 TI-RSLK 模块 7 - 讲座视频 - 有限状态机线路跟踪器
未学习 TI-RSLK 模块 7 - 讲座视频 - 有限状态机线路跟踪器
-
 未学习 TI-RSLK 模块 7 - 实验视频 7.1 - 运行 FSM 启动代码
未学习 TI-RSLK 模块 7 - 实验视频 7.1 - 运行 FSM 启动代码
-
 未学习 TI-RSLK 模块 7 - 实验视频 7.2 - 运行解决方案代码 - 设计更好的 FSM
未学习 TI-RSLK 模块 7 - 实验视频 7.2 - 运行解决方案代码 - 设计更好的 FSM
-
 未学习 TI-RSLK 模块 8 - 讲座视频第一部分 - 开关
未学习 TI-RSLK 模块 8 - 讲座视频第一部分 - 开关
-
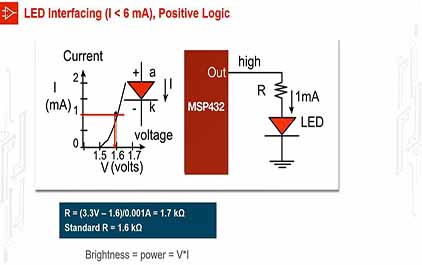 未学习 TI-RSLK 模块 8 - 讲座视频第二部分 - 连接输入和输出 - LED
未学习 TI-RSLK 模块 8 - 讲座视频第二部分 - 连接输入和输出 - LED
-
 未学习 TI-RSLK 模块 8 - 实验视频 8.1 - 连接开关和 LED 以及调试
未学习 TI-RSLK 模块 8 - 实验视频 8.1 - 连接开关和 LED 以及调试
-
 未学习 TI-RSLK 模块 9 - 讲座视频 - SysTick 计时器 - 理论
未学习 TI-RSLK 模块 9 - 讲座视频 - SysTick 计时器 - 理论
-
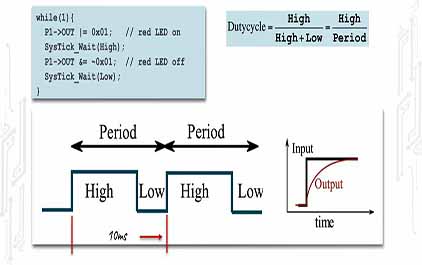 未学习 TI-RSLK 模块 9 - 讲座视频 - SysTick 计时器 - PWM
未学习 TI-RSLK 模块 9 - 讲座视频 - SysTick 计时器 - PWM
-
 未学习 TI-RSLK 模块 9 - 实验视频 9.1 - 演示通过调整占空比来运行检测信号
未学习 TI-RSLK 模块 9 - 实验视频 9.1 - 演示通过调整占空比来运行检测信号
-
 未学习 TI-RSLK 模块 9 - 实验视频 9.2 - 演示通过运行正弦波输出来调整功率
未学习 TI-RSLK 模块 9 - 实验视频 9.2 - 演示通过运行正弦波输出来调整功率
-
 未学习 TI-RSLK 模块 10 - 讲座视频 - 调试实时系统 - 理论
未学习 TI-RSLK 模块 10 - 讲座视频 - 调试实时系统 - 理论
-
 未学习 TI-RSLK 模块 10 - 讲座视频 - 调试实时系统 - 中断
未学习 TI-RSLK 模块 10 - 讲座视频 - 调试实时系统 - 中断
-
 未学习 TI-RSLK 模块 10 - 讲座视频 - 调试实时系统 - SysTick 中断
未学习 TI-RSLK 模块 10 - 讲座视频 - 调试实时系统 - SysTick 中断
-
 未学习 TI-RSLK 模块 10 - 实验视频 - 演示运行线传感器和黑匣子记录器
未学习 TI-RSLK 模块 10 - 实验视频 - 演示运行线传感器和黑匣子记录器
-
 未学习 TI-RSLK 模块 11 - 讲座视频 - 液晶显示屏
未学习 TI-RSLK 模块 11 - 讲座视频 - 液晶显示屏
-
 未学习 TI-RSLK 模块 11 - 实验视频 11.1 - 演示 LCD 界面
未学习 TI-RSLK 模块 11 - 实验视频 11.1 - 演示 LCD 界面
-
 未学习 TI-RSLK 模块 12 - 讲座视频 - 直流电机 - 物理
未学习 TI-RSLK 模块 12 - 讲座视频 - 直流电机 - 物理
-
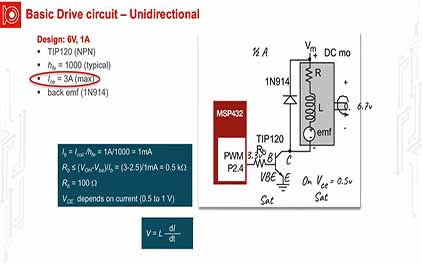 未学习 TI-RSLK 模块 12 - 讲座视频 - 直流电机 - 接口
未学习 TI-RSLK 模块 12 - 讲座视频 - 直流电机 - 接口
-
 未学习 TI-RSLK 模块 12 - 实验视频 12.1 - 演示电机基础知识
未学习 TI-RSLK 模块 12 - 实验视频 12.1 - 演示电机基础知识
-
 未学习 TI-RSLK 模块 12 - 实验视频 12.2 - 演示机器人以预设模式移动
未学习 TI-RSLK 模块 12 - 实验视频 12.2 - 演示机器人以预设模式移动
-
 未学习 TI-RSLK 模块 13 - 讲座视频 - 周期性输入
未学习 TI-RSLK 模块 13 - 讲座视频 - 周期性输入
-
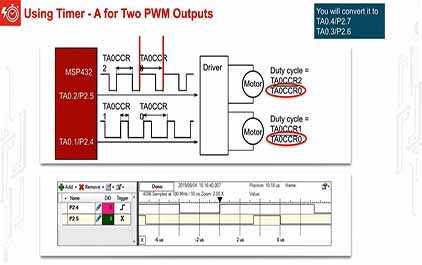 未学习 TI-RSLK 模块 13 - 讲座视频 - 脉宽调制
未学习 TI-RSLK 模块 13 - 讲座视频 - 脉宽调制
-
 未学习 TI-RSLK 模块 13 - 实验视频 13.1 - 通过计时器产生的 PWM 输出来旋转电机
未学习 TI-RSLK 模块 13 - 实验视频 13.1 - 通过计时器产生的 PWM 输出来旋转电机
-
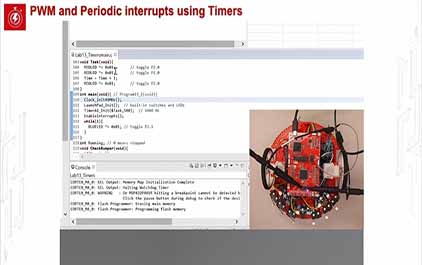 未学习 TI-RSLK 模块 13 - 实验视频 13.2 - 测量中断延迟
未学习 TI-RSLK 模块 13 - 实验视频 13.2 - 测量中断延迟
-
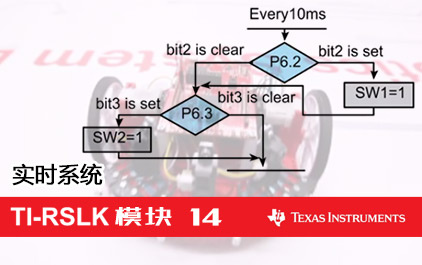 未学习 TI-RSLK 模块 14 - 讲座视频 - 实时系统 - 理论
未学习 TI-RSLK 模块 14 - 讲座视频 - 实时系统 - 理论
-
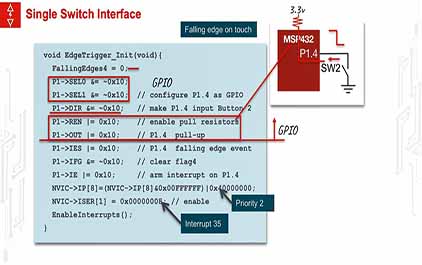 未学习 TI-RSLK 模块 14 - 讲座视频 - 实时系统 - 边沿触发中断
未学习 TI-RSLK 模块 14 - 讲座视频 - 实时系统 - 边沿触发中断
-
 未学习 TI-RSLK 模块 14 - 实验视频 14.1 - 使用边沿触发中断为碰撞开关提供实时响应
未学习 TI-RSLK 模块 14 - 实验视频 14.1 - 使用边沿触发中断为碰撞开关提供实时响应
-
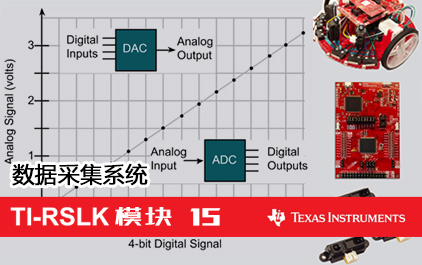 未学习 TI-RSLK 模块 15 - 讲座视频 - 数据采集系统 - 理论
未学习 TI-RSLK 模块 15 - 讲座视频 - 数据采集系统 - 理论
-
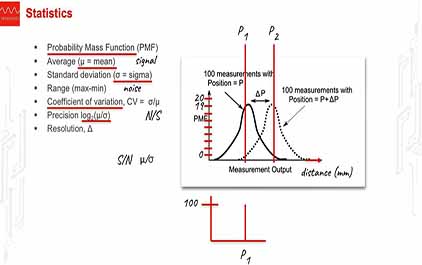 未学习 TI-RSLK 模块 15 - 讲座视频 - 数据采集系统 - 性能测量
未学习 TI-RSLK 模块 15 - 讲座视频 - 数据采集系统 - 性能测量
-
 未学习 TI-RSLK 模块 15 - 实验视频 15.1 - 使用 ADC 测试红外距离测量
未学习 TI-RSLK 模块 15 - 实验视频 15.1 - 使用 ADC 测试红外距离测量
-
 未学习 TI-RSLK 模块 16 - 讲座视频 - 转速计 - 输入捕捉
未学习 TI-RSLK 模块 16 - 讲座视频 - 转速计 - 输入捕捉
-
 未学习 TI-RSLK 模块 16 - 讲座视频 - 转速计 - 接口
未学习 TI-RSLK 模块 16 - 讲座视频 - 转速计 - 接口
-
 未学习 TI-RSLK 模块 16 - 实验视频 16.1 - 测试转速计以测量速度
未学习 TI-RSLK 模块 16 - 实验视频 16.1 - 测试转速计以测量速度
-
 未学习 TI-RSLK 模块 17 - 讲座视频 - 控制系统
未学习 TI-RSLK 模块 17 - 讲座视频 - 控制系统
-
 未学习 TI-RSLK 模块 17 - 实验视频 17.1 - 演示控制系统 - 积分控制
未学习 TI-RSLK 模块 17 - 实验视频 17.1 - 演示控制系统 - 积分控制
-
 未学习 TI-RSLK 模块 17 - 实验视频 17.2 - 演示控制系统 - 比例控制
未学习 TI-RSLK 模块 17 - 实验视频 17.2 - 演示控制系统 - 比例控制
-
 未学习 TI-RSLK 模块 18 - 讲座视频 - 串行通信 - UART
未学习 TI-RSLK 模块 18 - 讲座视频 - 串行通信 - UART
-
 未学习 TI-RSLK 模块 18 - 讲座视频 - 串行通信 - FIFO
未学习 TI-RSLK 模块 18 - 讲座视频 - 串行通信 - FIFO
-
 未学习 TI-RSLK 模块 18 - 实验视频 18.1 - 演示 UART
未学习 TI-RSLK 模块 18 - 实验视频 18.1 - 演示 UART
-
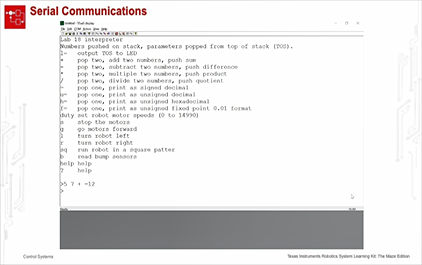 未学习 TI-RSLK 模块 18 - 实验视频 18.2 - 命令解释器
未学习 TI-RSLK 模块 18 - 实验视频 18.2 - 命令解释器
-
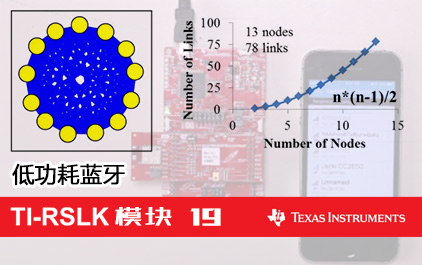 未学习 TI-RSLK 模块 19 - 讲座视频 - 低功耗蓝牙 - 无线
未学习 TI-RSLK 模块 19 - 讲座视频 - 低功耗蓝牙 - 无线
-
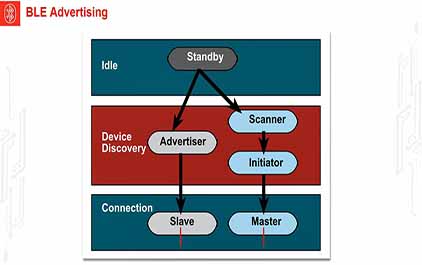 未学习 TI-RSLK 模块 19 - 讲座视频 - 低功耗蓝牙 - 理论
未学习 TI-RSLK 模块 19 - 讲座视频 - 低功耗蓝牙 - 理论
-
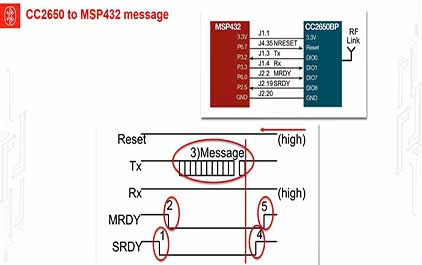 未学习 TI-RSLK 模块 19 - 讲座视频 - 低功耗蓝牙 - 简单网络处理器
未学习 TI-RSLK 模块 19 - 讲座视频 - 低功耗蓝牙 - 简单网络处理器
-
 未学习 TI-RSLK 模块 19 - 实验视频 19.1 - 演示 BLE
未学习 TI-RSLK 模块 19 - 实验视频 19.1 - 演示 BLE
-
 未学习 TI-RSLK 模块 19 - 实验视频 19.2 - 与机器人通信
未学习 TI-RSLK 模块 19 - 实验视频 19.2 - 与机器人通信
 视频简介
视频简介
TI-RSLK 模块 17 - 讲座视频 - 控制系统
在该模块中,你将学习控制系统的基本概念。