人工智能
最新课程
- MSPM0G 系列 MCU 时钟配置:在 LED 闪烁的情况下动手操作
- Code Composer Studio™ v20 入门
- 双 DMA 正弦波环回:在 MSPM0G 上实现从 DAC 生成到 ADC 捕捉
- MSPM0G3507 动态 CRC 配置和实时验证
- 视频系列:tiarmclang 编译器
- 汽车应用中的 Jacinto™ 7 处理器
- 可以在 2 分钟内实现无线基础设施应用
- TI 超声成像系统电源方案介绍
- TI 连续血糖监测(CGM)方案介绍
- AI 智能眼镜充电的需求与续航力
热门课程
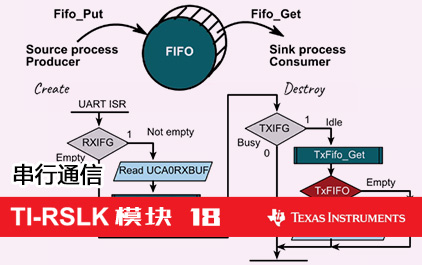
TI-RSLK 模块 18 - 讲座视频 - 串行通信 - UART
[音乐播放]
大家好,我是
这节课我们将介绍通信。在通信问题部分,我们首先来讨论一下
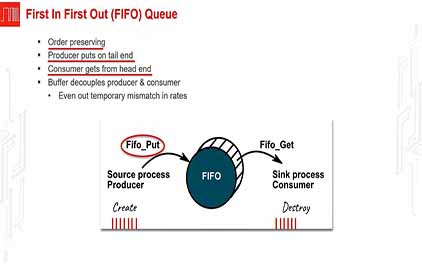
一种叫做先入先出队列的
重要数据结构。
我们现在要做的是,创建该缓冲器,
以便在数据流过系统时
存储数据。
这是一个非常重要的数据结构,
一般用于复杂的系统,具体来说
是通信系统。
接下来,我们将讨论一些定理
和一些性能指标。
现在,我们开始吧。
好的,这个先入先出队列
是一个缓冲器,对吧?
它会存储数据。
我们将会在能产生数据的
系统中使用该缓冲器。
这个系统可能是一个输入设备,
也可能是一个软件。
在另一个流程中,会使用或销毁
数据。
它会处理这些数据,然后这些数据就没用了。
我们要做的是,在数据从生成器
传输到使用器时,将其临时存储在
此
在执行放置操作时,我会将其放在列表的末尾。
在执行获取操作时,我会从列表的
开始位置进行获取。
通过这种方式,该结构便成为了保序结构。
它的优点是,我可以对两个流程的执行
过程进行解耦。
所以,我可以生成几个,使用一个,然后再生成
几个,再使用几个。
通过这种方式,便无须再以锁步方式
运行生成器和使用器。
我可以对在整个系统中流式传输的数据进行缓冲。
这将是一个非常重要的结构。
下面,让我来演示一下它是如何运作的。
这个系统会有很多实现结构,
这个是最简单的结构之一,但它是一个缓冲器。
我为它分配了固定大小的空间。
这是一个有限缓冲器。
这个
我不会让它一直走到
会更简单。
但我将会使用两个指标。
一个告诉我最早的数据的位置。
GetI
即这条线的开头,
它告诉我下一个要获取的数据是哪个。
第二个指标叫做
该指标指向这条线的末尾,
即我接下来要放置数据的空白点。
在这个特殊的例子中,如果
则表明该
让我来演示一下,
我将会把五个东西放进
然后取出五个东西,
我们来看看这个操作是如何实现的。
首先,我将会把数据放在
PutI
所以,这便是进入这个地方的全部数据。
然后,我将会把它存储在
然后使
下一个数据,我将会放在这里。
所以,如果我再次调用,第二个数据便会
出现在这里,且
然后是第三次调用。
这是第一个。
这是第二个。
这是第三个,也是最新的一个。
但是,现在我需要将
因为这是一个有限缓冲器,需要重复使用数据。
然后,我放置第四个数据。
这是最早的数据。
这是最新的,对吧?
这便是我放入的数据。
每次放置后,我都会将数据存储在
并使
很明显,我将会把下一个放在这里。
因此,这是第一个、第二个、第三个、第四个和
第五个。
在这个特定队列中,GetI
PutI
下一个东西的位置。
让我们调用
同样,当我调用
所以,这个数据会被删除,
我将会读取
我将会获取下一个。
也就是这个。
我读取
在取出这个后,我需要
将
如果您记得,这是
我放入了这五个东西,并且已经删除了
第
最早的数据是第四个。
所以这个会被删除。
同样,我会第四次调用
现在,GetI
调用
这个会被删除。
现在,GetI
表明该
虽然现在与开始时的
情况不再一样,但是,如果
在函数开始时等于GetI,便表明
FIFO
好的,这里的几个流程图
从根本上解释了我刚刚在
换句话说,它可以存储
如果有
如果有
将数据存储在
同样,对于
如果
我将会返回清空错误。
如果有
从
并返回成功的结果。
所以,系统有许多实现方式,
但这是相当简单的一个。
让我们来讨论一下一个有趣的定理,利特尔定理。
让我们以桥为例讨论一下,好吧?
假设
汽车将会通过这座桥,对吧?
我们将会定义
存在的汽车的总数,
也就是数据包的总数。
我们会在桥上的FIFO
数据包,并有一个处理中的数据包。
因此,系统中总共有
如果我们考虑每秒钟的数据包到达率,
或者也可以想成每秒的汽车到达率,
然后我们使用利特尔定理来定义平均到达率,
也就是数据包的平均
响应时间。
相当于,如果汽车驶往桥的前面,
要用多少秒
才能通过这座桥?
如果我知道数据包进入我的系统的到达率,
而且知道桥上的汽车总数,也就是,
FIFO
再加上
那么,我便可以使用利特尔定理来评估
N、λ
例如,R
数据包数量,也就是
FIFO
除以进入系统的数据的到达率。
这样,便可以确定系统的平均
响应时间。
从这个角度来看,队列是我们处理
数据流问题时的一个有趣的
处理和研究对象。
综上所述,我们使用
生成器和使用器之间暂时存储数据。
我们了解了利特尔定理。
这是从实验
我所做的便是定期测量FIFO
我执行了很多次,因此您可以
看到成千上万的测量数据。
在本实验中,不存在
数据包的数量超过
因此,我们可以看到,在这个特定的
或者说
这个特定的生成器和使用器用例中,
如果我选择大小为
这便是在实验中绘制这个直方图的
好处之一,因为您可以了解
怎样才能确保FIFO
希望您喜欢本次实验。
这是一个非常重要的实验,
介绍了通信的概念以及数据
如何在系统中流动。
祝您学习愉快!
[音乐播放]
-
 未学习 TI-RSLK 模块 18 - 讲座视频 - 串行通信 - UART
未学习 TI-RSLK 模块 18 - 讲座视频 - 串行通信 - UART
-
 未学习 TI-RSLK 模块 18 - 讲座视频 - 串行通信 - FIFO
未学习 TI-RSLK 模块 18 - 讲座视频 - 串行通信 - FIFO
-
 未学习 TI-RSLK 模块 18 - 实验视频 18.1 - 演示 UART
未学习 TI-RSLK 模块 18 - 实验视频 18.1 - 演示 UART
-
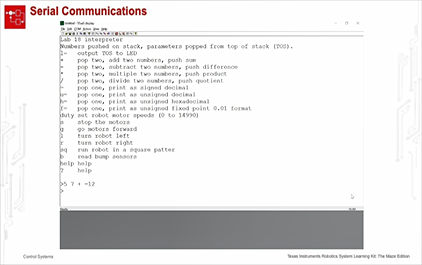 未学习 TI-RSLK 模块 18 - 实验视频 18.2 - 命令解释器
未学习 TI-RSLK 模块 18 - 实验视频 18.2 - 命令解释器