线性系统的性质
Loading the player...
将在30s后自动为您播放下一课程
线性系统的属性 、那么我们的介绍 熟悉 我们的房地产空间配方、 以及我们如何从中提取认证 信息、 包括矢量 和矢量值、 然后是动态 响应 之间的连接时, 优先考虑 MOSFET 表示法和 transfe 函数表示法。 该段 会进一步变小、 并检查 状态空间公式的属性。 尤其是、 非常重要、还有几个 想象 不到的其他人。 最不可避免的属性 是稳定性。 您可能会看到非常清晰的图像 我所说的稳定性。 很明显 、对于稳定的系统、 对于连续时间系统 、甚至是传递函数 稳定意味着什么。 您在看到它时就知道它。 它要么 是一个细长的 gthat 仍然绑定、 或者它不 会重新绑定、这很好。 但对于 stat 空间描述 其中我们有一 个内部变量、 稳定性分为几个级别 认知很重要。 当您进一步讲德语时、 如果您继续了解双头螺栓 非线性系统、 你会发现稳定性确实 是一个非常可怕的概念。 有这样的系统 外观 就像它们是稳定的、 看起来就像它们一样 同时在重写。 因此,我需要从 国家的角度解释稳定 空间说明, 特别是从状态开始 CEO 观点 然后,还有交流损耗。 这些是对资产空间描述的唯一性。 这些称为可控 性和可观察性。 它们不适用于 etransfer 函数描述。 但它们确实适用于 空间描述。 它们非常重要。 因为当我们稍后使用 进行设计控制系统时 状态空间模式、即系统 无法控制、 我们的努力将是徒劳的。 稍后 、当我们开始设计时 估算器或观测器 、这是相同的、 如果无法 观察到我们开始使用的系统、 同样,我们的努力 也是徒劳的。 我们无法从 无法观察到的系统估算 estat。 控制能力 和可观察性 是 我们稍后需要的重要属性。 现在、事实证明、稳定性 以及可控性 和可观察性、 所有这三项 如果 我们可以执行、就会有非常清晰的可视化效果 特定的近亲 DOF 变换 在系统上调用 da 模式分解。 我将向您解释 一下实际的模式分解 方法。 但是、如果您可以执行 eout、则会执行所有这些属性 您会非常清楚、 并且有好处 也是如此。 因此、我们将从 模态分解开始、 我将向您展示 所介绍的属性 以及 其他方面的术语。 然后 、我们将再次查看标准化的实现。 我向您展示了一 种、phas 可变规范形式。 事实证明、它 是另外两个被称为的位 可控制的规范形式 和可观察到的规范 因为此处是三角波形。 这就是为什么这个部分 恰好出现在那个部分之后 控制 能力和可观察性。 然后 是我要做的最后一件事 这 是一个 fairl yshort 部分、 最后要介绍的是冲头 下一个教程、我 将会或多或少地 每个教程都 将基于该教程。 它是一个双质量系统。 它由一 个有两个质量的机械系统组成 耦合在一起、 这样当你推动 水体时、其他质量就会移动。 但 两者之间存在某种能量交换 质量。 结果是振荡。 这是一个很好的、易于视觉化的系统。 它具有很多动态特性 让这些教程 变得有趣 这三种运动。 所以,我要启用系统。 驱动 ZVS 转换。 现在、我想先 解释一下这个概念 矩阵。 当矩阵使用 dfor 变换时、 您已经看到 、在 n 维度中、矩阵具有尺寸 n 乘以 n 矩阵为方形。 因此 、如果存在转换 在 三维空间中、从一个矢量到另一个矢量、 变换矩阵执行 三维变换。 例如、在这里 、我们有一个矢量 V、 它不由矩阵 T1运行 将矢量 t oa 变换为不同的矢量 V tilde。 因此、V tilde 是指向 不同方向的点 Gin 因为 它是由矩阵 T1进行操作的。 现在、T1、如 Wel las V 和 V tilde、 将以该坐标系的项 s表示 或者二者都是复数。 例如 x1、 y1和 z1、它们 可能是正交坐标 它代表矢量 和变换 权衡关系。 现在、让我们想象一下 、我们什么都不会改变、 但所有 这些信息都是坐标系 演示。 我们不使用 x1、y1、z1、而是使用 x2、y2、 Z2. 嗯,现在,相同的 tw omatrics-相同 的两个矢量 具有 slightl ydifferent 表示法。 因为它们的元件 将会不同。 因为它们 虽然指向相同的方向 从理论上讲、它们 在中重新呈现 不同的坐标系。 以及变压器 矩阵 从 V 移动到 V tilde、 这也会有所不同。 因为它的协调 帧发生了变化。 它在做的是相同 的事情、 但它是在 adifferent 坐标系中执行它的。 矩阵 T1和 T2 试用相似的矩阵。 它们可以实现 相同的变换、 但它们在 adifferent 坐标系中执行它。 它们与 所谓的旅游相关 相似性变换。 具体而言、T2 i 序列到 M、再到-1、 T1乘以 M、其中 M 是 相似性变换。 它将 Matri x 从一个坐标系变换 另一个坐标系。 且在 500 MHz 下,其 IP3 为 [听不清] dBm 时 不是吗? 您可以看到矩阵 M它必须进行测量。 它必须具有 与 T 相同的名称尺寸、 因为 T2的 esame 尺寸与 t1相同。 但是、当 你看到它时、M 乘以-1、 考虑相似性变换。 它将在 一秒内进入 com ein。 请注意,这是一个重要的属性, 那么、让我 花几分钟时间来讨论它、 难以仿真。 可以找到类似 的变换矩阵 M、它 采用 T1并使 T2对角线。 如果您可以 执行该操作、则会出现该情况 是 产生的许多好处 系统的电感。 该特定坐标系。 但 为了实现这一点、t1 必须具有一 组完整的特征。 否则、您可以 对 T2进行 tdiagonalize。 如果 T1没有一 组完整的特征向量、 您不能具有对角线 T2、 但您可以接近它。 出现的仿真形式、 称为 Jordan、用于 mrepresentation 稍后我会介绍。 但现在让我们想象一下,我们 已经不会有一整套特征的特征 这种 SoM 相似性变换可以实现 从而 使产生的 diagona lmatrix t2 该矩阵是对角线、bit 具有更进一步的属性 即您可以 对元素进行范围内的操作 对角线 Matri 的斜线、使其如此 以及系统的效率。 类似 的转变 这对你来说是一个 scolumns,它们本身就是这样 T1的特征向量。 这里有一些重要 的信息 一些特性。 如果 T1具有一 组完整的特征向量、 矢量 是定义的 CPU 独立 这些矢量 扫描用作列 以形成类似 的变换矩阵 M 因为 您知道、对于尺寸来说是可以的 你 有 n eigenvalue sin t1、t1是 n x n、 并且 您已经设置了完整值。 您有一个特征矢量。 每个特征都对 RHAS 中的元素感到羡慕。 因此、通过将这些列、 即 M、M 的列进行设置 尺寸也必须为 n b yn。 并通过使用 Matri x 实现相似性 变换、T2斜 线对角线、但不仅仅是 对角矩阵 T 1的特征值将是元素 对角线的对角线。 现在、在 我们了解该信息之前、 我 将向您介绍如何操作 您 可以使用状态方程进行状态变换。 现在、假设我 将一个状态方程式进行了打字 对于基于 关节状态选择的系统 影响。 我之前告诉过你 ,没有什么特别的 状态元素。 大家想用什么都可以。 那么、让我们假设 您做出一个选择、 它对 您来说并不是很有效、 您希望将它们更改为 不同的元素集。 没有理由不能这样做。 变化可能 会因所发生的事情而产生 称为状态变换。 那么、假设您使用的是 x 、并且您希望进行转换、 改用 v。 vis a different -- 我是说它是一个状态矢量、但 我现在将其称为 v。 它与 x 通过 这个矩阵 M 相关、即 现在是 n 的任意矩阵 那么、我们要做的是将 这个直接置于状态 等式、x 点等于 x plu SV。因此、左侧不是 x 点不再出现、但它是 M 时间 SV 点。V 点是新状态 等于 AMV。 MV 只是插入之前 的 xwas,加上 v 乘以 u. v 不变。 现在、我们要做的是 、我的 SWE 将对两侧进行预乘法 与 M 的倒数相反、如果 您可以的话、现在这是一件好事 M 由特征向量组成。 因为 M 肯定 会反向。 因此、您可以 从 M 中找到反向 它是正方形的、因此尺寸 是我们所需要的。 爬虫 程序会以 M 的倒数进行预乘、 您得到 v 点等于 m t othe -1、乘以 M 次 五、看,类似 的状态转变 矢量。 加 n 到-1 乘以 v 乘以 u 我们执行 了相似性变换 在电压矢量上的优先权。 并猜测 负1 AM 矩阵的 MTO 值 变为负数的区域。 它就是带宽。 它 将在前导代码中具有该 eeenvalues 对角矩阵 我们要将其命名为 LPO。 让我们将 M t othe -1B、B1称为。 现在、这是状态向量 Rinto 转换状态。 我们现在需要集中讨论 输出方程。 可以执行相同的操作。 但它要简单得多。 因为我们不会 将 ETO M 反转。我们需要的一切 将 x 替换为 M 时间 SV。我们将其称为 C1。 因此、C Time M 将 变为 t obe c1加 v 乘以 UD 不受所有这些影响。 那么、现在我们有了 stat 公式和输出 该 新状态的 I nterms、v、 v 恰好是多少。 现在、独特的选择 -那么、这里有 无限选择。 您可以随意选择名称。 因此、我们不会将任何 特定状态绑定在一起。 您可以在 一个和另一个之间切换频率。 但对于这种声波 ,v 的元素 有一个特定的名称。 它们被称为 系统的表情。 典型系统运行 I nCharacteristic Set of Patterns、 梯形脉冲。 这些模式称为模式。 它是 状态矢量的电子元素的唯一选择 这些称为模式。 这之所以很 重要的原因是 您将看到 每个模式的时间 与所有其他模式完全解耦。 这种变换、 独特的变换 其中您使用了 eigenvector 列的 Mmatrix 转换为-使用 我的 neffect 矢量变换。 这称为调制 分解。 在以后您了解到 自己可能希望 第一个是 、事实上这些模式是不耦合的 彼此之间、可 提供非常清晰的可视化效果 放大数模转换器和输出之间的信号。 不仅是这样、而且通路 从状态中的输入端 到输出 的状态要清晰得多 如果 你刚刚采取随机状态、你会更好 矢量 MAPS 动态特性 更易于解决。 因为存在 标量、而不是矢量。 您可以对 随时间变化的运动进行非常简单的视图、 它使 系统的动态变得更加清晰。 因为通过公开这些 值、 您知道哪些是主要模式、 这一点不太重要。 请记住 复平面中的电子滤波模式、 复数中左侧的特征值 比 那些衰减得多 在右侧、它们接近 虚轴、 如果它是一 个持续计时系统、那么它们就会被执行 与我 FIT 的离散时间系统并联。 您还可以 获得更清晰的见解 介绍了 tw 属性 更早的可控 性和可观察性。 我 认为通路暴露在外的原因 实现平衡。 该过程在 一段连续的时间内类似 奈奎斯特路径。 只是曲折 的特征值是不同的。 那么,让我们来执行它。 我们将编写 模态相似性变换 我 现在将其称为 W、 因为它是一 个非常具体的转换矩阵。 M、但 我想将其称为 W 由 列 sof W 组成 独立 的特征向量的特征向量 矩阵 A。因此您不需要 对列进行调整、 每列都有 n 个元素。 这是一个 n x n 矩阵。 我将为 该矢量添加符号 因为经济转型也是如此具体 以及 称为模式的独特选择。 我将为 符号 q 进行 E过渡期、 元素 wil lbe Q1到 q sub n 有 系统的模式。 是的。 就是这样。 现在 、存在 r表示 法变化 我想让您知道。 这是 EMI 滤波器部分。 这里是 输出端。 因为这 是一个独特的选择 的列数 W、正如我说过的、我们最终得到 了一个令人激动的新系统 矩阵 DMS 这是一个交流电机。 Lambda 将沿其前对角线包含 A 的特征 那么、写入这些方程 、Iguest 这就是它们的外观。 扇 出的模式矩阵包含在其列中 A 的特征向量 和频谱矩阵、 因为它称为 Lambda 、所以我对角线矩阵在这里 特征值位于 主对角线上、 所有的 释放都是零。 模态矩 阵 是应用 于这两者的名称。 现在、模式输入矩阵是 W 到-1乘以 v 我们将把 W 插入 状态变换公式 那个方程。 我已经解释过的 λ。 现在、输入矩阵 、W 至-1 v。当您 进行此分解时、 将 该输入的各个行分开很有用 矩阵。 因此、我一直将这些行 称为 sbeta 1、beta 2 至 β n 这些是 WTO 的负1 v 行,即 为什么我这么写。 可以将其视为变量。 但实际上 、它们是行矢量、 现在、输入矩阵的第行中有 n 个。 输入 矩阵的 Beta 1和 beta n ar ethe 行、 W 至-1 V 因此、这会 影响您的状态方程 看起来像完整格式。 左侧的模型矢量的导数 等于频谱矩乘 以模态矢量、加 然后、这些是 新模式输入矩阵的行 s. 但我想它们是 一个矢量乘以输入矢量。 如果您愿意、它 将为我提供测试版 捕获所有 电子输入到特定模式的耦合。 然后、Lambda 我捕获 从 Qi 到 Qi 点的动态。 那么、您现在看到了我的意思、即完成 去耦。 如果您可以用 此表单编写 estat 公式。 那么、这是模 态输入矩阵。 这就是它在 到达单个模式时的外观 您得到的方程。 那么、现在请注意 、这个 Lambda 我出现在这里、这是 是完全标量。 关键点是 动态不耦合。 输入矩阵。 现在、模式响应、之前 的每个状态派生 可能涉及 所有其他状态。 因为 状态矩阵可能有一个 da 行 它 一直具有非零元素。 但现在你得到的是我 只需一个一阶 差分方程、 涉及相同的模式。 其他模式不 会产生任何效果。 这是模式的分辨率。 因此、它是用来 修复瞬态响应的特征值。 这将为您提供 模式演进的增长或衰减。 然后、参与 积分涉及 β I 这样我们就可以 得到响应的整形 是 确定该值的矢量 通过 与 B.的关系 输出矩阵 I sthe 乘积为 C 和 W 这对我的想法很有帮助 作为 单独的向量。 此外,可能会发生击穿,这可能 因为该 wil 向上乘以向量。 因此、伽马1至 GAMM an、单独的矢量、 每个矢量对 成个单独的-一种单模式 所有输出上。 那么、这就是我 应该看到的样子。 我是说它们是向量 、但考虑它们 现在至少是标量。 正如我所说的、每个伽马我 都会闪烁一个特定的模式 所有输出上。 以便输出矢量 等于所有这些乘积的总和。 因此伽马1乘以 Q1、plu sgamma 2乘以 Q2、依此类推。 现在、我认为这个图 将把它全部绑在一起。 因为这是我们 所做的所有图形。 我们已更改了显示方式 完全 独立的套件 状态、每个状态 都是完全的 去耦所有其他的。 现在为 729。 因为 Qi 取决于 y 点、反之亦然。 以及空间与所有输入之间的耦合 由相应行的低确定、 输入矩阵的输出。 以及所有输出之间的耦合 由模态输出矩阵的 I colum n 决定。 那么、您现在可以看到吗? 您已经获得了非常清晰的可视化效果 所有输入 如何影响一种模式、 以及 MOD 如何影响所有输出。 这 种表示非常明显 发生的情况。 现在一切都正常、 前提是您已经完成了 一整套 eigenvectors。 如果您没有 、那么您可以使用的单向方法是这样的 如果您使用 了树形特征值。 那么、在我向 您介绍如何操作之前 您使用这些 信息来描述 我 想要的属性 o fa 系统 简单地轻触一下 、如果您有问题、会出现什么问题 有一个去生成系统矩阵。 它只能通过 反复的特征值来实现。 即使这样、我 也可能不会发生。 你可能会幸运 、可以说、你已经成功了 才会出现退化。 但您仍然有 一组完整的特征矢量。 或者您可能运气不好 、丢失一个或多个 铜。 因此、系统会发生退化。 当您遇到 eigenvectors 时、您必须 如果您要执行 TA 模式分解、 您必须 替换 mby、替换缺失的 具有 被调用的矢量的矢量 广义特征向量。 这些 仍将是真正的特征矢量的正交。 但它们不会 满足矢量的要求 我 在前面展示的公式、它是什么 是负 λ i、乘以 WI。 我们寻求 了一种微不足道的解决方案。 因此、它们会对 特征去变体进行泛化。 您可以在网站上找到这些信息。 有一个很长的 yprocess 可以找到它们、 我不打算 在今天的研讨会中讨论这些内容。 但一旦找到 了它们、您就可以使用它们 实现平衡。 但频谱矩阵、对 角线 eigenvalues 不再 是真正的对角线。 它 将在斜升对角线中有一些元件、即1。 这意味着电 极二极管不会完美 去耦所有其他的。 将会有一个小的耦合 EBIT 开启。 Matxri 的形式 具有该对角线、 但某些受支持 的对角线等于1。 它们称为 Jordan 矩阵。 矩阵、即 生成的系统矩阵、 或频谱矩阵、其中 有 Jordan 块。 现在 、在时会出现可能的差分排列 您开始丢失矩阵。 但从根本上说 、特征检测器的编号是 实现的最大值 取决于您 的解决方案 获取公式 A minu si 乘以 λ i 再乘以 WI α1α2 = 0。 这就是你发现了这些嫉妒者的方式,你还记得。 你这样做是为 lambda i 的选择 现在、我的 λ 一定 是可耻的、您可能会失去解决方案。 您可能没有完全 独立的解决方案。 您得到的数字取决于 在空空间维度 o fthis matrix 上、A 减 I 次 λ I. 空的 spac eDimension 会告诉您 您 将要获取多少个电子矢量 该特定的 Lambda I. 在本例中、 有一个整数 我叫 calin ghi、告诉你 可用 特征向量的数量 放大器驱动电路。 且 numrbe 介于1、 你将始终得到 1、而 Mi 特定 特征值的多重性。 如果您幸运、您可以使用 GE TA 全套、在这种情况下 你已经得到 了完全不一般的东西。 我们无需担心。 但是 、如果您没有这么做、 嗯、如果 你只有一个、你 需要这些通用 的去 igenvalues、 最后得到完整 的 Jordan 表格展示。 如果 您具有介于1和多重性之间的 你最终 会看到 Jordan Blocks 出现。 频谱矩阵 x 中有特定的块 它们具有1的超级对角线。 但它们并非全部为1。 它们中有些被压入。 让我来向您展示 一个有关这方面的快速示例。 这可能是一 个 Jorda 挡块 与特定的值相关联 具有一定的多样性。 同谋 是数字 对角线上的元件数。 您可以看到 、所有元素都是0、 但这几个除外。 这称为 Jorda nblock 或 Jordan 矩阵。 因为这是唯一的矩阵。 例如 、这里是一个五阶系统、 它具有三个特征值。 这有两个主要目的。 我有两个在-2处 、两个在+ 3处。 这 是一个不稳定的系统、1位于-1。 那么、在这个 scase 中、会出现什么 是 针对负2处的 tw oeigenvalues、 有一个约旦集团 的 kof A。你看到了吗? 它位于对角线上、 因此特征值 XY 尺寸更小。 但我们 需要的广义的 eigenvecto 在那里放置了1。 然后 、对于3、还有相同的细 gg 一个 Jordan Block 出现 在 ghere、对角线上有3秒、 对角线中为1。 然后是单 个特征值 给了我们一个 与它相关联的嫉妒。 因此 、您会在右下角得到一个很好的-1 i 类似情况。 现在、我将执行 一个快速教程、 只是为了向您展示 如何使用模式分解。 一次、它不再是 这些降压转换器的基础。 当 我清除其他一切时、请与我保持联系。 在本例中、我们在教程6.1中 分解-- 我不知道我做了什么。 为此我 道歉、我按下了一些东西 我不应该把 它分解 组成模式。 那么、很显然、这是 一个三阶系统。 我不知道它 将是怎样表现的。 但它显然有两个输入。 因为输入 Matri x 中有两列。 因此、我们有三个状态、 我们有两个输入、 我们有单 输出、因为 输出矩阵 C 的形式。它有一行。 因此必须有一个输出。 它具有 thre ecolumns、因为我们 知道有三种状态。 输入矩阵为0 - 转换矩阵 很抱歉、是0。 它包含两个元素。 因为有两个输入。 它有一行、 因为有一个输出。 那么、让我们分解 成它的组成模式、 看看会发生什么情况。 那么、首先、我们 要做的就是 hthen 使用 与我相同的方法构建系统 之前在 MATLAB 中展示的。 在我们进行 模分解之前、 我将绘制其响应。 我们将看到其 响应变化 模式分解后。 首先、我 将要构建 阶跃响应 、并绘制三种模式。 现在问题是 、这里有两个输入。 那么、阶跃响应 、问题是-原因 它 有两个 Pste 输入。 因为当 您执行一个步骤时、MATLAB 会对 LDO 产生什么影响 具有两个输入的系统上的响应是 有两组结果。 一个是 施加到第一个输入的 ste、 而第二个保持为0。 另一组结果 、当第一组结果保持为0时、 第二个应用 了阶跃输入。 因此 、这里将会有状态图的 tw oset。 它将反映 状态的维度 由此产生的矢量、 状态矢量结果。 我们可以开始了。 仿真结果如下。 上图是 三种内部状态的演变 当我们有阶跃应用 程序 dto U1、U2保持为0时。 然后 、在这里的底部图中、反向是 这些是 随时间推移的状态解决方案 因为 U1保持恒定、 而 nu2施加了阶跃。 现在、我们要做的是 perfor ma 模式分解。 我们就是通过这种方法来连接它的。 此 CLC 只清除 工作区中的任何内容。 这使事情 对我们来说有点整洁。 然后、我 将再次执行 EIG 指令。 请记住、这是 从中提取的特征值。 但当您使用 这两者的结构时 电 容、电容和电容参数 将返回模态矩阵 W、 频谱矩阵 λ。 嗯 、键盘对 lambda 没有注意。 那么、我将使用大写的 L 这是两个矩阵 、n x n、3 x 3 在这种情况下、将返回这些值。 您为其提供系统 mmatrix a、而不是仅提供平衡 意味着不要平衡 特征检测器、 我的意思是,我只是把 电子贸易机会这样做。 没有关系。 现在 、你已经把 W 变为原来的值。你可以 在类似 的变换中使用它 提取模式输入 和模式输出矩阵。 请记住、模式输入 Matri xwas W 到-1乘以 B 因此、我们将反转 W、 并将其乘以 B 我是雅斯特- 嗯、 我将断开它。 因为我很感兴趣、所以我 将行视为向量。 稍后您会看到。 然后、模态 outpu tmatrix 为 C 乘以 W 然后 、OIS 将代表它们 作为电流 LSB。 我们来操作一下。 您将看到 A、B、C 和 D 消失、 我们最终获得 L 和 MIM 0和 D 我不知道为什么 w EDID 不会结束-好的。 好的。 因此、它所做的就是再次为 我提供 A、B、C 和 D。 但这点我 是作为频谱矩阵的点。 这是 以指数值的 gof 表示的 λ 实现平衡。 这就是 EN/UVLO 引脚。 很好。 我想知道为什么它会被转置。 这实际上是正确的形式。 我不得不思考 为什么它被转置了。 但这是 输入矩阵的巨大形式。 因为它有两列。 有两种方法。 然后,还有交流损耗。 因为 其中有三种状态。 然后是 outpu tmatrix、模态输出矩阵、 透射 性 nmatrix 仍然为0。 我们现在将 执行相同的操作 我们在 Carrie dout 模态分解之前做过。 我们将进行预设 、并绘制状态。 现在,这是问题所在。 对于这种特定的状态选择、 因为我们有一 个完整的对角化光谱矩阵、 我们现在必须具有完全去耦内部状态。 每个状态 都取决于其自身的状态。 因此、我们得到了等于 λ i 乘以 Qi 的 Qi。 它们耦合在一起。 它是第一 个 orde rdifferential 等式。 这里没有其他东西。 您从过去就知道 、一阶解决方案 差分均衡 呈指数级。 因此、当我们计算 并解决这些问题时 对于阶跃输入、我们应该找到 1减去指数衰减 代码。 我们得到的确实是这样。 那么、这些是状态 、以及它们现在是如何演变的 变化情况。 因为它们 彼此去耦。 您可能会看一下 并思考、嗯、好的。 他告诉我们。 那么、什么。 可能系统也发生了变化。 但我 的观点是、它只是这样 系统实际动态的状态变换 不变。 换言之、 整个系统 无论 我是否表示、行为都完全令人感到羞耻 使用 SoM 耳本选择的状态、 或这个特定的选择。 我将向您展示这一点。 现在,我要 做的是,我要 绘制原始系统。 Y1的图、这是 原始系统的输出。 第二个传感器已经成功连接。 好的、这 没什么特别有趣的。 这就是系统的行为方式。 现在、我在 这里的 GTO 中所做的是、 这是一回事。 我将绘制 该图 Y2的顶部、Y2 是发射 分解的输出。 我 希望、所有这些变化 是该图的颜色。 它应该从蓝色变为绿色、 因为它是同一个系统。 它只是国际 动力学 以不同的状态选择表示。 这就是调制 分解为我们所做的事情。 [INAUDIBLE]? 使用 GA 模式分解的主要原因 从 mthe 输入到输出的路径 更清晰。 该属性意味着 可控性的属性 和可观察性、 可预测性等 更容易实现可视化。 看到 GPIO。 没错,这是问题的关键。 因为它会引导我 了解接下来将要做的事情。 [INAUDIBLE]? 是的、这是可能的。 [INAUDIBLE]? 嗯、它会使 引脚感到它 可能会将注意力集中 在非主导模式。 因此、它可能在这方面有所帮助。 或者您是否希望 简化系统 通过减少它的 orde rof、它可能会对您有所帮助 做出该选择。 因此、我 需要在控制设计方面提供帮助的原因有很多。 [INAUDIBLE]? 是的,确实如此。 [INAUDIBLE]? 嗯、有点像。 对,很接近了。 但我想摆脱 超前和滞后的想法 补偿器、也 是根轨迹的除法器。 因为在 系统中-我昨天介绍过 其中我们使用 doutput 反馈、我们 必须 关闭闭环 特定线路上的极点称为 loci 的复平面。 我们 可以更改的唯一精简 gg 是增益、沿 这些轨迹移动轨迹。 状态反馈控制的一大优势 您可以在 复平面中任意选择您喜欢的任意值 放置极点。 您具有极大的灵活性 接近 的环形极点所在的位置。 您 正在使用的栅极、FAC 而 不仅仅是输出中的状态矢量 好处。 因此、我认为这有助于 推进这一决策过程 极点的选择。 现在、我 将稍后更多地使用该小数位。 但我想 在一段时间内继续保持 kabout 稳定性。 那么,有两种 类型的函数。 在 我们继续之前、我想告诉您、 并了解如何使用它们。 第一个问题是,我们 可能会立即这样做 视为稳定的系统。 这一制度占有 财产 称为渐近 cti 稳定性 这意味着它的状态 i nthe initial condition 随着 时间的无限变化、 将收敛于该 电子平衡点。 因此、这相当于一 个稳定节点或一个稳定焦点 在我 之前向您展示的相位纵向中。 因为这种状态 会跟随某种路径。 这是一个稳定的焦点、 最终会随着时间的推移而出现 它稳定地稳定 在平衡点。 它称为渐近稳定性。 对于什么、有一个字的 ydefinition 这意味着、就 可以在多大程度上取代初始条件而言、 它与 平衡点收敛的事实。 因此、具有 连续时间值的系统 小于0、或者 如果是 rdiscrete time eigenvalue 小于 1的模数、具有属性 渐近稳定性。 现在、在 本幻灯片中、我能不能 做一些看起来 很明显的事情 您很清楚、 这一点非常明显。 因为它稍后很重要。 在稳定状态下 、对于渐近稳定系统、 如果是连续时间、您 知道稳态是 由 T 等于0的 x 点定义。 这意味着 estat 不再改变。 它达到 了它的固件点。 那么这是稳态。 但请注意、如果它是 离散时间系统、 存在陷阱。 因为我 在稳定状态下的意思 是 nex tstate 没有不同 输入和现态。 状态 XK 加 1与 XK 相同。 因此、当你保持 稳定状态时 对于分立式系统 、重要的是 右侧 不再是0。 这将在 我们看设计时再次出现 控制 系统中的稳态的高电压基准。 但我想提醒 您注意这一点 一个重要的差异。 实际上 、这是唯一的一个 稳定部队的差异 时间和 离散时间系统之间的差异。 因此 、稳态定义存在差异。 但无论如何、我认为您 可能[听不清] 想象一下,“那是一 种很棒的稳定。 现在 存在某种稳定性、 它位于 phas 纵向图中 其中平衡 点被称为中心。 一般而言、我 称为 Lyapunov 稳定性。 Lyapuno v컈 뚨 所说的是 如果您将初始 状态从其平衡状态中移位 然后让它运行、 前提是您没有 让它从 该状态转得太远、 它将对 状态进行收敛、 也可能不会达到无穷大。 它可能会保持 在平衡的每一个特征中 不 会在比赛中到达它。 这是 一个系统示例 它具有复杂的共轭 值、如果它是连续的 时间、或单 个转盘上的电子值、如果它是离散时间。 因为这些振荡 是持续的。 它位于边界上、不稳定。 它称为预翘曲。 有时您会看到具有 Lyapunov 稳定性的系统、 被称为稳定的是 Lin 的 Lyapunov 感。 这不是我们担心 的事情。 但术语会不时出现 、尤其是 非 线性系统的应用。 但执行 此操作的系统、在本例中 它是二阶 的、它的相位纵向会是 属于 中心的类别、 它具有利亚普诺夫稳定性。 现在 、绘制了两个车床图 就输出而言, DPWM 模块 2 和 此电路的频率响应。 我将讨论的是、没有 WIS 如何涉及输入。 因为 输入的有效性允许 我们将在 内部和外部进行区分 稳定性 首先、 内部稳定性是 耦合的属性介于 输入和状态之间。 它有时称为边界 性状态稳定性、 或 BIBS 稳定性。 有时、它是回调 式内部稳定性。 因为我们在谈论内部 变量集 称为状态。 提供 RA 有界输入、 状态保持 受限 获得 BIBS 或内部稳定性。 如果您解决 稳定性的均衡问题 主动能量传输。 显然、您正在寻找 外部信号。 以及 外部稳定性 当有界输入仅 产生有界输出时定义。 您具有 BIBO 稳定性。 现在、因为输出均衡 仅是代数方程 涉及到状态、则会提供 有界输入 有界状态稳定性、您会 自动获得有界输入 宽输出稳定性 因为在 该状态下、动态特性仅在那里 但不会相反。 这并不一定是一 个关键问题、因为系统是这样的 外部稳定、 内部稳定。 要确定该值、 您需要确定 状态如何从 内部耦合到输出、 主动能量传输。 您可能具有内部状态、这些状态 会像疯狂的那样振荡、但 不会耦合振荡 到输出 电流、因为存在 是输出矩阵中的0个元素。 因此、内部 稳定性是肯定的 可保证外部稳定性 、但不会相反。 好的, 现在、让我们来了解 一下可控性 10K 欧姆的电阻器。 稳定性概念也 会进入这种情况。 我有她 的 eis 四阶 已 执行模式解调后的系统。 它与 我之前展示的图表类似。 因为每个 表情都是完全的 与所有其他组件不耦合。 输入和 每种模式之间的耦合 由 W 减1 B 矩阵的 sw 行确定、 以及从 EAC 模式到所有输出的耦合 C Wmatrix 的列、这些伽马元素。 现在、 这是 W 的异或响应行 负1 B、因此 Bi 转换器 是非零值和伽马 I 非零、很显然 、tmode 是通过耦合的。 因此、您可以说是 因为输入 耦合到该模式、 我可以影响该模式 来减少输入电压。 因此、我 所说的模式是可控的。 因为 CW 矩阵的相应 gcolumn 非零、当该 模式移动时、它是 某种程度上会影响 至少一个输出。 因此、这 种模式的情绪 观察到的相关事物。 模式1被认为是 可控制和可观察的。 您可以看到我 在这个图上进行了详细的了解。 因为您知道该 异或响应矢量、 Beta 1和 γ 1为非零。 现在想象 一下伽马2为零的位置。 这意味着该模式不 会耦合到输出。 我们无法 通过观察输出来确定 gSimply Q2是否稳定 EOR 为不稳定模式。 因此 无法观察到 tmode。 但由于 β 2是非零、 因此它与输入耦合。 因此我们可以对它施加影响。 这 是一种可控但无法观察的模式。 当 reverse 为 true 时、您可以 看看 模式3会发生什么情况、β 3是零、 但伽马3不为零。 因此、这种模式是不可控制的、 但至少可以观察到。 最后、有一种模式 、它与任何东西都是解耦的。 它是一 种无法控制的模式和一种无法观察的模式。 因此、这些属性 非常明确、 模式分解后、它将立即开始运行。 首先、 正如我说过的、它们的重要性是、 您无法确定 任何相关内容 内部可控性从 传输中循环伺服 功能描述 这些只是 状态空间描述中的属性。 幸运的是、物理 系统 控制 器和可观察的、 这意味着、当您 从头开始构建 astate 空间模型时、 某种系统、 即实际系统本身 那么这里的电压将大于 VOH。 但您的模型通常 包含一些简化 或一些假设、意味 着模型可能不会 具有这些属性。 因此您无法 控制 系统或观测器的型号 您的系统模型。 如果您选择的 stat edoes 具有这些属性、 然后执行 astate 变换 不会更改属性。 因此 、您使用的 wha tstate 选择无关紧要、 证明其正确性。 和可观察性 是系统独有的、 而不是选择状态。 你往往有各种原因使稳定部队有问题。 最常见的原因是您 忘记了有极点 在 您的转账职能部门、您可以在此处取消或取消预订 或 等效的传递函数 说明中有 偏斜极点和零点。 但由于 其他原因、您可能会运行 int oit、 例如、对状态进行明智的选择、 或可能是国家数量。 这些东西也可能会降低 可控性 简称 WCT。 首先是包络。 总结 一下左侧的两张幻灯片 sago IAR。 因为只是很喜欢 动态、 从 输入到模式的连接路径、 β 1和 β 2列矩阵矢量 为 SPI。 Q1和 Q2 与输入进行爬电耦合。 那么,这是一个 RAM 地址。 而系统在黄昏中是无法控制的 功能模式。 但它是具体的模式 2、这是不可控制的。 因为模式2未 连接到输入端。 Beta 2是一个0矢量。 这是 IC。 因为这个 特定的特征值 位于右半平面。 这意味着 系统不稳定、 无论如何、GWE 都无法做到这一点。 因为我们无法 控制不稳定模式的通量。 这种薄 的 gg 可能不是很明显 如果您只需要随机 选择状态变量、 以及完整的可变状态 器描述。 但 它可以避免雪的存在 系统中存在不稳定和不可控的仿真二极管。 这将在稍后引发问题。 因此,如果您 在这里有电阻, 分类是 可控和不可控的 非常清楚。 您只需查看 rnonzero beta i 矢量。 这 是一种查看事物的方法。 还有 一个代数测试 适用于一般情况。 代尔拜 ctest 就是这样的。 您首先必须构建 可控制性矩阵 从现在开始、我将调用 P可控性矩阵 这样。 现在、这是 calle da 分区矩阵。 我想这是 昨天的 Matri x代 数笔记中的内容。 一个分区 Matri xcontains 元素 它们本身就是矩阵。 eis 上的这个特定结构如下所示。 它是 B、A 乘以 B、A 平方 B、一直到 A 到 n 减1乘以 B。让我们细小 它的尺寸。 B、您知道、i n x r matrix。 它有 n 行和 r 列。 a 是方形矩阵。 因此它不会 改变行数 有很多类型。 AB 将 会进行仿真、因此是 n x r 矩阵。 A 平方 B、类似地、n 除以 r 因此每个 分区都是 n 乘以 r 因此 、整个东西中都有 n 列。 您有 n 行、您 有 n 次 r 列 一个示例。 然后、你所做的 是、你看一下它的排名。 现在、请记住 矩阵的侧面 是 最大非零决定因素的尺寸 任何位置。 那么 、对于这个矩阵、你可以得到的最重要的排名是什么? 你不能大于 n 因为它中有 n 行。 它有 n 乘以 r 列。 那么、您有一个输入。 它将 是 bEAN n x n matrix。 这就是 EMC 问题。 如果您有10个输入、它 将是10n 的10倍。 但它不能得到大于 n 的 bigge、因为你 需要一个方形 Matri xto 具有一个决定因素。 因此、你 可以拥有的最大的 RAN 是 n 现在、如果这个特定 矩阵具有秩 n、 系统是可控的。 您是怎么做的。 对于离散时间系统 也可以这样做, 唯一的区别是 电位变化、A 的 C、 B 的伽马。 否则、您将构建 控制 器矩阵、并对其进行评估 完全相同的方式。 您 可以说有 SoM 的表达方式。 如果您只有一个级别 o fv、其中 v 小于 n 然后您知道您 只能使用 v 可控模式。 您有 n minu SV 不可控模式。 因为其中 n 减 v Beta 检测器为零。 还有一些人在可 控制性指数中进行了定义 因为 它是必须具有的最小数量的分区 添加、直到您获得全排名。 嗯、无论如何、这是第三 个可控制性指数。 现在、可观察性非常 相似、令人惊讶的是、 令人震惊的相似之处。 我有一个问题。 请说。 [INAUDIBLE]? 是的。 [INAUDIBLE]? 当然。 [INAUDIBLE]? 好的。 [INAUDIBLE]? 你会说 滴滴不会改变。 它 将永远到达一零。 你们得到的是这个吗? 是的。 就是这个[听不清]。 它将如何激发? 是的。 答案 是、我在数学上讲这个东西 将永远保持为零。 实际上,我们没有这样做过。 存在影响 系统的噪声和扰动 实际上、您只是 不知道。 它不会保持为零。 但你已经确定了你 不能影响它的 FAC 低电压。 因此、无论发生什么 情况、您都无法更改。 什么都不会改变。 因为会 有激发它的 SoM e扰动。 然后实习 YIT 将会增长。 但从数学角度讲、您是对的。 没有什么可以激发它的。 因此、理论上、它 永远不会保持为零。 但这不是必需的。 是的。 这是 ROM。 音频正常吗? 是的。 好的。 因此、继续 观察、 没什么特别的。 我们解决 了可观察性的均衡问题 放大数模转换器和输出之间的信号。 它是 CW 矩阵的列 s 它为我们提供该信息。 如果它们都是非零、 那么-即使是模式 通过输出耦合。 因为 γ 1、即 refxample、决定了 Q1与 所有输出耦合的方式。 在左侧、有 一个可观察的系统。 它仍然是一个不稳定的系统。 因为如果 N 大于 0, 它是一种 弱实时系统。 大家可以看到这一点。 因此、该电子模块 将会振荡。 但至少我们可以检测 输出端的振荡。 这是 可观察性的定义。 右侧是 I hav EAN 不稳定系统。 我认为它具有相同的模式 、因此具有相同的特征值。 但这是不可观察的、 因为伽马2是0。 CW 矩阵的第二列为0、 因此、secon dmode 未连接 任何输出。 我们 没有什么可以检测到什么 第二种模式将会执行。 这 也有一个代尔拜克特尔。 它涉及形成 顶点矩阵 时间反转函数。从现在起、P Q 将为 这两个矩阵保留 dd。 因为我们现在非常需要 GTO。 现在形成 了分区 从 C 转置、转置、 转置、转置 转置等。 您在 该矩阵中查找运行 kof n。 如果您有它、 则可以观察到 nthe 系统。 如果您没有 该系统、则无法观察到系统。 离散时间有一个并行 替换为 C 的系统 现在有两 个相关的附加属性。 其中第一个是 我的扇贝稳定性。 IO_SUP 与 RX_SUP 相同。 但问题是仅针对 不稳定模式。 我来举一个例子。 这是一个系统、它是 一个无法控制的系统。 因为我们知道 FIRS tmode 与输入不耦合。 因为 Beta 1为0。 因此、这个 modeCAN 执行它所需要的任何操作。 w eCAN 无法影响这个模式。 但它是一种稳定模式、 至少它是稳定的。 但是、第二种模式是不稳定的。 但它具有一 个非 Zer obeta 2矢量。 因此、它通过 输入耦合、 因此、w eCAN 会影响它。 我们可以稳定 输入的 b y 操作。 因此、我 可以控制该系统、 需要的电压电平。 但至少它是可以稳定的。 但可以设计它。 还有另一 个与此相同的 mter。 但它会应用于输出。 它称为预翘曲。 它是可观察的、但只能寻址 到不稳定的模式。 实际上、它是 Sam esystem、 但在这里、您已经获取 tgamma 1非零值、 第一种模式是耦 合到输出。 第二个问题是可靠性。 现在、这里的第一 种模式是不稳定的。 因此、它 是一个可检测的系统、 降压-升压解决方案的大门。 第二项要求源于 虽然它不可观察、 因为它是稳定的 则可以说器件具有 ELDRS。 这意味着、如果 涉及到一个 yinternal 振荡、 系统内部任何不稳定的东西、 至少您可以检测到它。 因此、我通过 两种方式定义了可控性和可观察性。 我已经定义了稳定性 和可检测性 是可控 性和可观察性 但仅解决 不稳定模式的问题。 下面我们快速测验一下。 因为这 真的很有趣。 我们将对 结构特性进行调查 四阶系统的性能。 我 没有任何 IDE。 因为我不记得 本教程是如何实现的。 那么,让我们看看两种情形。 首先 、我们创建系统。 这里没有 什么令人惊讶的东西、 仅使用 SS 和 A、B、C、 D首先、我们要介绍 进行稳定性分析。 现在 、MATLAB 中有一个手录。 您不必担心 像 eigenvectors 这样的事情 和特征值、以及在 左半部分计划中的工作情况、 或右半平面。 您只需键入即可保持稳定。 是稳定的、它真的需要所有的东西 、不是吗? 因此、 您所做的是、您键入的是稳定的、 或者它是稳定还是不稳定。 是的。显然这 是一个不稳定的系统。 我们还不知道它。 但它是一种电路外的 EOS。 现在、我们要在 GTO 中做的下一件事是检查可控性。 我首先要做 的是我正在看 显示了片上 SRAM 的大小。 这将告诉你维特 尼-现在如果你在这里键入1、 它将告诉您 行数。 如果您键入2、则 会显示列数。 因为 它们的尺寸为1、2。 但我知道 AIS 是一个方形矩阵。 因此、这并不重要。 这将告诉我 系统的尺寸是多少。 当然、在 本例中、它是4。 然后、在这里、我 介绍了重要的一行、 因为这是 可控制性矩阵的构造。 CTRB 构造 控制性矩阵 您 所需的两个抹香 为其提供 系统矩阵 A、 和输入矩阵 C 因此,我们 现在对 P 退了 我只需要了解 P 的级别 与 A 的尺寸相同、它 是系统的等级 和系统的尺寸。 如果是、 则系统是可控的。 如果不 是、则是无法控制的。 很高兴这 是一个可控制系统。 因此 、在那里的某个地方有一个不稳定的仿真二极管。 但至少它是可控的。 因此、您可以说 该系统是可稳定的、 尽管它不稳定。 现在、我们将为 可观察性做类似的事情。 我将使用构建 可观察性矩阵 Q 为其提供 A 和 C 矩阵、 然后再次检查排名。 希望运行 的 kwill 等于4。 不幸的是、它不是。 等级小于4。 因此 、系统无法观察到。 并尝试 去探索神秘之地 在这个系统的后面、我们 将进行模式分解 你会发现这是为什么。 那么、我们将 共同定义 A 的 EIG 为我们提供一 个模态 d光谱 矩阵、 然后计算调制 线性输出和输出矩阵。 这是下一个脚本中的目标。 我们可以开始了。 现在、在我们 进一步讨论这个问题之前、 一些属性 现在变得清晰。 因为我们所做的都不 是模态分解。 我们显然拥有 完整的一组特征值、 和完整的特征 矢量。 由于所有 这些值都不同、 因此,我们知道我们 不会成为一整套特征的特征。 但是、如果您看 一下它们、左半平面、 左半平面 、你得到的是加1。 这就是 系统不稳定的原因。 这里有一种积极的价值。 3号为正。 嗯、我们知道它是 一个可控系统、 所以 我们不应该感到惊讶 einput 矩阵的所有行都不为零。 但我们也知道我 无法观察到、 这意味着 模式的 SoM eof 不是 噪声有多少。 输出 矩阵的头两列 为0。 因此伽马1和 伽马2都是0。 但伽马3和 伽马4不是0。 我们已准备好 [? 我们有 ISO-21848。 我们有 ISO-21848。 现在、 我告诉过您的其他一些属性 稳定性 和可检测性。 那么、让我们 先处理稳定性问题。 这 是不可扩展的系统吗? 是的。 米歇尔说是的。 每个人都能实现 经济转型的稳定? 它是稳定的、 因为所有模式都是如此 RTI = 参考了输入 因此 、无论模式的音调如何都是不稳定的。 它通过耦合。 因此它 可以稳定下来。 这是可检测系统吗? 为什么没有呢? 好。 嗯,请思考一下。 可检测性是可观察性、 但仅解决此问题 ECG 波形总是延迟。 因此、我们不是处于 稳定模式的中间位置 不稳定的情况。 嗯、它是第三个 不稳定的模块。 因此、我们将提高 可检测性、 可观察性。 我们需要 CW 矩阵非零的第三个色谱。 就是这里。 通过观察 gthe 输出、我们得到了 至少得到 了这个东西的电子信息 变为负数的区域。 这 是一个稳定的电子和一个可检测的系统。 但这并不理想。 这是无法观察到的 、整体来看。 因此 、该系统具有这些属性。 好。 我希望我们几乎就在那里。 我们有两种形式。 我不打算对这个进行人工操作。 因为我已经完成了。 这几乎是午餐时间。 这是 phas 可规避的规范形式。 这两者之间的任何不同之处 我 在上一张幻灯片中展示了相位 变量规范对于 mon、它是标题。 它称为控制 器 ecanonical 表单。 您可以通过 我向您展示的过程来实现这一点 开始, 您会得到矩阵的非常识别的电子结构。 您可以从 系统矩阵中获取该值 其中所有 的不祥因子系数 显示在底部行中。 除 超对角线外、矩阵的其余部分为0、 即1。 这是因为状态的选择、 即状态选择 是相位。 B 矩阵、输入矩阵 、为0、除了最后一个矩阵。 C 矩阵、 输出矩阵、 包含 分子的系数。 当您看到它时 、您就知道您是 处理控制 器 ecanonical 表单。 它称为自动生成该表单 可控 今天 下午、我们将使用这种形式 设计状态空间系统。 现在 、有一个类似的形式、称为 可观察的规范形式。 我将 很快地向您介绍、 告诉你 滴滴的关系非常密切 与可控 性表单非常接近。 该矩阵是 可观察到的规范形式、 现在我将调用 OCF。 好。 您有 CCF 和 OCF、 您可以看到这些缩写。 OCF 系统矩阵 与 CCF 系统矩阵相关 锁存器。 这就是所有的不同之处。 现在来看看关断, 对于观测 表例形式、 输出为 经济过渡期 控制 器规范形式的矩阵、 这两者也与 转置相关。 在某种意义上、可 控制的输出矩阵 是 可观察输入矩阵的转置、 反之亦然。 接下来,请看这里的 观测 表例形式的矩阵、 它与输入矩阵相同 可控制的 canonica lform、只是转置。 因此、如果您了解 一下音调描述、 您已经自动 获得了另一个、 如果您现在有 转置、OCF 和 CCF。 现在、 当我们来到这里时、这些东西令人非常愉快 进行状态空间设计。 CCF 更改了状态 反馈的设计 非常简单。 和 OCF 表格让 观察员设计人员 简单的提示。 现在它们是 calle dcomp配套 表单。 它们通过 这些转置相互关联、 我在 上一张幻灯片中向您介绍的内容。 但是、这种关系我 非常强大、 您最初可能想象的更强大的功能。 这种关系的名称 称为 duality、 这意味着这两个系统 被这些矩阵所描述 相反的信号线。 因此、您可以选择 其中一个的可控性 检测 对方的可观察性、反之亦然。 因为如果您在寻找 P 和 Q 矩阵、 它们的关联 方式与我的关联方式不完全相同。 请记住、P 矩阵是 B 分区 B、A 乘以 B、 乘以 B 可观察性矩阵 I twas C 转置在 B 位置、 和 A 的转置 I nplace。否则 完全相同。 因此、当您检查 其中一个的可控性时、 您实际上正在检查 另一个是否具有可循环性。 这种类似的并行功能有助于我们以后的工作 详述这一点。 因为使用 的技术是这样的 电压反馈控制器的设计 与 您用于观测器设计的完全相同。 这是一件充满力量的事情。 因为您只 能获得一组流程、 您可以执行这两个作业。 在这一部分的最后, 我 将向您展示一个非常简短的教程 可能会出现什么问题。 有一个术语"最低 限度实现" 这意味着您找到 了具有最小空间矢量的空间矢量 可能的尺寸。 以及您的模型可以使用的 GIS 的功能 在那里有状态、什么 都不做。 保存的操作太多。 您可能有 第三阶系统。 但你不小心 给了它四个状态。 当你这样做的时候 ,事情可能会出错。 通常 会出现问题的是您 失去 了我刚才讨论过的一个属性。 例如、您会丢失 可控制性属性、 这意味着 UCA 无法控制系统。 因此、您必须开始 确保已经完成了 具有可控性。 如果没有、请看一下。 您是否在处理 实现问题? 为了说明这一点、 我将执行它 以组织形式提供、教程6.3。 这意味着、对 可控性和进行调查 三 阶的可观察性属性似乎无害 一个输入。 因为 B 矩阵是 acolumn 矩阵、并且有一个输出、 因为 C Matri 坐标轴是行矩阵。 那么、让我们在 MATLAB 中查看这一点、看看会发生什么情况。 因此 、从一开始就没有什么令人惊讶的、 我们将开始 建立这一制度。 命令窗口中没有任何显示。 但这些是 工作区中的 Matrice swover。 我们已经构建了系统。 现在、我们将确定 首先可控性、 使用过去 用过的技术, 构建 可控制性矩阵、 并确定其等级是否为 等于 系统矩阵的大小。 如果是、 则系统是可控的。 如果它不 是-嗯、它是不可控制的。 但令人高兴的是、这是一个。 因为系统 mmatrix 是3 x 3。 这是 P 矩阵。 我们正在寻找它 中的大非零决定因素。 实际上、它会发生 这种情况 具有非零决定因素。 因此 、该矩阵的排名为3、3等于3。 因此、这 是一个可控系统。 现在、让我们继续、为 可观察性做些令人遗憾的事情。 我们已经知道 n 是3。 我们不必重新计算它。 可观察性、这 是可观察性矩阵。 不幸的是、最大 非零决定因素是2 降低了 2 毫瓦。 在这里、它具有2级。 2小于3、这 是一个无法观察到的系统。 现在、为了找出 原因、我接下来要做的是什么 查看 传递函数的 stat 部分。 因此、我将 使用脚本转换 S STO TS 要转换为 transfe 函数描述、 然后 TS 从 它构造 G、即 etransfer 函数。 我们来看看这个。 简单地说、好的、 到目前为止没有什么明显的。 它是一个三阶系统 、其中包含两个零。 现在、我们接下来要做的是、I SWE 将使用此 ZTK 脚本。 请记住、这是 一个显示极点和零点的函数 信息作为数组。 因此、这将告诉我们 分子是什么 分母是相同的。 这将显示 极点和零点。 此时、您 可以看到存在问题。 因为 这里有一个阻抗极点。 一个极点位于 S 等于 sminus 1、另一个零点 时间极点开始。 据说这 是一种微不足道的认识。 现在、我在这里看到 一个 TA 相当简单的系统。 系统会变得更 复杂、 订单数量众多。 找到这些东西有点难。 有时您不需要 转至传递函数 以查找它们。 但很高兴 MATLAB 为您提供 了一个名为 minreal 的脚本。 看到、 MATLAB 花费多少钱-花费多少钱是惊人的 MATLAB 工作将从它中取出。 MinReal、您将为我提供 传递函数。 在本例中、G1是 ZTK 形式、然后是 将返回 rtransfer 函数、 控制器,即这里的 EC。 在本例中、它将为 我们移除该消除极点。 现在、我们有 一个二阶的 transfe 函数。 我可以继续 对状态空间进行疏浚 评估它的稳态响应。 现在、我 在做它的方式、你会的 这也是一件事 、就是回来 这些系数数组进行比较 该设计的链接。 这与该 TS 数据不相关。 它返回枚 举符和分母的数组、 将系数转换为数组。 然后使用 TF 到 F STO 返回另一个方向。 将函数 转移到状态空间、 它将这两个数组作为 对四个矩阵的返回值 空间描述中所需的所有信息。 我们可以开始了。 现在有 了秒序系统 以国家空间形式表示、 这是一种最小的实现方式。 最后一件 行李简单地确认了 我们现在处理 的是可控和可观察的 转换器。 它与 之前应用的测试 SWE 相同、 构建可控 性和可观察性矩阵、 并在 本例中检查它们的侧面是否为2。 因为 系统的顺序减少了1。 我们可以开始了。 2是 系统的 orde r. 我们有一个2 x 2矩阵、其等级为2。 这是可 控制性矩阵。 因此、我们仍然很好。 现在是可观察的 Matri 坐标轴2 x 2、它有一个秩。 现在、我们也开始 了可观察性。 因此您可能会遇到问题。 这些问题往往 会降低可控性 简称 WCT。 因此 、我们在本次课程中几乎没有遇到过这种情况。 然后、我们将 准时地点餐。 现在、我要在 GTO 中使用的系统非常一致 今天下午 、对于教程、 是一个机械系统。 它基于像 这个这样的双重 sma 系统、其中 有两个质量、M 1和 M2、它们在坐着 并在 某种情况下自由滑动。 因此、您可以想象 这两个质量 金属块或桌子上的某种薄格。 我们可以影响 他们的立场 从 质量 M1的黄昏开始。 当我们这么做时、 很显然 M1将移动。 其位置称为 Y1。 当它移动时、它会 在 M2上施加力、 因为它通过 该弹簧减振器与它耦合 组件 现在、这些 sprin gand 风门值 耦合的情况 耦合非常轻微潮湿。 这意味着、当你在 M1上给它一点细微差别时、 M2将 像这样进行归零、 它将在很 长一段时间内继续执行 lik ethat。 因为 那里有非常轻的阻尼。 那么、现在、如果我构造 它的 da 模型、 就像这样、这可能 会永远地滑动。 因为 没有什么东西可以阻止它。 我所做的是、我已经对 DIN 进行了几个摩擦术语的说明 因此、我 当然不会 你知道 会有摩擦。 这种化石 正在发展 死机有两个原因。 一个是 因为它有点潮湿、 另一个原因是 存在滑动摩擦 这 将最终在这两个质量中获得成功 为了平稳的停止、我 只需给它一个踢。 现在、我 想变量 o finterest 是 Y2。 我想我 在这里的工作就是我 力控制、 施加到 M1的力、 希望专家组 Y2 在我希望的位置。 当然、在 不受控制的无反馈中 情况、某种程度的操作 计、实际上是死算。 但 您将在今天下午晚些时候看到 Ron 控制的应用、 它是令人惊叹的超精确度 使用 gof M2的位置、即使有 它们 之间的间接耦合、 它们之间的轻微阻隔耦合。 现在 、我选择它的原因是 您可以将 此处发生的情况可视化。 它 有一个很好的统计器空间描述。 我将此作为新 版本的书中的附录。 它还可以从 网站下载 附录。 因此、如果 您访问网站和您 查找 该书的版本、 如果您不 想购买这本书、 您实际上可以在 此处重新创建附录、 附录 E、它实际上为 您编写了所有这些内容。 这是 PDF 格式的电子附录、 欢迎 您下载。 而不进行详细 介绍 是运动方程。 这就是这个空间方程的样子。 这是二阶的。 您有 一个4x4系统矩阵。 什么 情况下发生呢? 太好了! [INAUDIBLE]? 抱歉。 您在附录中给出了它。 这里有一些 mor 电子信息。 我能不能事后跟你谈谈这件事吗? 因为我没有 完整的推导 而设计。 这将有所帮助。 是的,可行。 是的。 我可能应该这么做。 我还没有完成 整个推导过程 而设计。 但方程 中的"sher"几乎是正确的。 它们 不是完全正确的原因就是这样。 我也可以告诉您。 看到、我刚刚应用 了牛顿的第二定律 以获取这两项。 这里也有一个摩擦力。 因为这是 关于运动的电子方程 第一个质量的值、其为 输入力 u 其中涉及的内容。 我已经将 状态指定为 第一 块块块块块块块块的位置及其导数。 那么、这是第一 个质量的速度 DOF、 以及 secon dmass 的位置及其导数。 因此、当我为 x2点形成电子方程时、 乘以加速 因子 nx2点等于所有该批次。 问题是 这里的 mas sterm 出现在左侧。 因此、您将会遵守 这些其他条款 乘 以 M1除以除法、 左 侧有 x2点、如果您愿意、 控制器,即这里的 EC。 而薄 的 gthat 出错了 我忘记 了将该项除以 M1。 那么、在 这里的方程上、这不应该是1。 这应该是1除以 M1、对吧? 因此、无论如何、我在 六个月前发布了该内容。 我了解 了这种情况的结果。 因为有 七或八个像 附录 E 中的不同部分和所有拓扑。 我们的到来 非常漂亮。 然后我开始了 BAC KTO 在我发布了 Dar ning 之后、我查看了它。 天哪! 我忘记了 M1。 您知道 我为什么要离开它? 因为 M1是1千克。 因此 、我在人生中有一次很幸运。 因此 M1是1千克。 好。 现在、让我们快速 学习本教程、 您将看到该 系统的行为、 或没有行为、具体取决于 您的行为定义。 好的, 好了。 所以、我们要做的 是非常精细的非常细化的 gery。 我已在脚本中更正了它。 在这里、我们将使用 SS 函数创建模式焊盘 以创建状态空间模型。 就是这个。 现在、我要做的是 执行模式分解 就像 我之前所做的那样。 我们将看到 模体的外观。 现在、它是一个拥有 一整套特征器的系统。 因为我 现在有一个完整的对角线模式矩阵。 但您已经可以使用 这两个特征值 非常复杂。 因为大多数 esmall 实际组件、 但想象中的分量 非常虚幻。 因此 、您在这里有一个较低的振荡。 我们可以 从中看到的 在第三种模式下存在一个非常小的数字。 这可能意味 着系统不稳定。 但这并不理想。 这低至 MATLAB 的分子分辨率。 这是一个0 eigenvalue。 我们有一 个模式线性输入矩阵 它包含一组复杂的术语。 因此、我 可以控制系统、这很好。 您可能会想象 它是什么样的系统。 和模型 outpu tmatrix 类似 一个复杂的术语集。 因此、它也是 一个不可伺服系统。 到目前为止一切顺利。 我们可以像 以前一样,以同样的方式来核实这一点。 那么、让我来证明 它是可控的 它很复杂。 现在、我要做的是 不执行初始条件 评估它的稳态响应。 我将从 x 矢量中转到 t*、它 因为这里有 四种状态。 我将从 该状态中提取第一状态和第三状态。 现在、我已经在其中添加 了这两者之间的初始分色。 因此、这个 y0 更远、 这表示初始 化两个质量 被距离隔开。 我想我使用 大约一个仪表。 它是一 个非常好的双系统、这个。 那么、当我将其添加到该位置、 然后减去第一个 从第三种模式 中、我从 Y2减去 Y1、 并添加初 始偏移。 因此、这将为 LME 分色 质量的影响。 当我运行它时、 您会看到 EIT 是一个振荡系统 确实。 这是一个曲线。 但您将 看到它会下降 我们开始控制它。 总数值非常高。 因为你给了我 一个微移、它将会运行 就像那样。 这就是 EN/UVLO 引脚。 让我 第二次运行 BAC KA、然后向您展示 我使用了什么初始条件。 这个矢量、我在这里 对第一个位置质量进行了调节 稍微偏右一点、 这是一个正向。 第二个是 左侧的易碎位。 因此、我稍微压缩了一下 sprin GA、 然后放开。 因此、这 种平装的东西压缩了它 为 10 伏或类似的电压, 它会停止所有该运动。 这是 IC。 现在、我们将绘制 单个质量位置。 这是 所涉及的绝对的排列。 因为我 将 Y2的开始考虑在内。 Y0被添加到 Y2中。 在 我们应用该测试时、您将看到行为是如何的。 好了。 那么,这是 ROM。 它要重得多、 而且它的 SGOT 是一个更大的摩擦 大电压系数引起的。 它的 衰减速度非常快。 这是质量 M2 、它受到影响 到更大的程度。 很好。 这 两种情况下会发生什么情况 会在 该幻灯片上缓慢地摆动 Way: 他们在 幻灯片上进一步休息了大约法米 比他们开始时要好很多。 因此、我想您可以通过 执行 BOOING 来实现这一目的、就像这样、 它将 稍微振荡一点。 然后它最终进入 GTO 移动并休息。 就是这样。 如果 我们有如此倾向、 构建该图的波特图。 为此、我们启用 了传递函数 表示 好,就是这。 现在、这证明 存在 SAN 集成。 因此、极小 的 leigenvalue 为0。 然后、我得到 了共轭偶极 和 一个实极点和一个实0。 所有这些东西都可以 在波特图中进行初始化、 样子的拓扑。 因此、我们有一个积分器 、负90度、然后 有一 个共轭共轭极对、它 提供了这个和那个。 然后、这里有一个极点、 真正的极点和一个真正的0 在这里的某个位置。 这些是校验器的校验器。 我们将 更详细地进行检查 此常见问题解答 现在 剩下的是唯一一个细牙 是我最喜欢的部分 、即测验。 类似 矩阵有什么共同之处? 它们相似吗? 因此、它们 是通用的。 [INAUDIBLE]? 是的、它们确实如此。 是的、它们确实具有 名称值的数量 帧周期和帧数。 这不是 我要找的答案。 但这是一个很好的答案。 我 要寻找的答案是他们 用 二表示 Sam 的系统化 不同的坐标系。 但 你绝对是对这种情况的。 在过去,这主要依赖串行总线 模式表示法的两个优点。 我想此时-- 简单 您是对的、简化。 从输入 和输出到输出的路径 可视化效果要明显得多。 [听不清] 对,是的。 因此、由于 我们刚才所说的第一个属性、 证明其正确性。 可观察性、 以及可检测性 10K 欧姆的电阻器。 所有这些东西 都更容易实现可视化 在构建 可控制性矩阵时、 例如 ,寻找一个排名。 因此 、对这些内容进行视觉化要容易得多。 对于离散时间系统、内部稳定情况如何? [听不清] 您处于稳定状态。 说得对。 稳态输出。 因此、内部稳定性、请调用 另一个名称。 Michelle 知道、它具有 有限的输入、有限的状态。 那么、只要输入受 限、状态是否受限? 如果是、它具有边界 输入受限状态、 或内部稳定性。 这种离散时间会怎么样? 那么 CMTI 呢? 我们对系统的看法是什么 它是否具有内部稳定性? 对我来说、内部稳定性确实 是一个错误。 输入怎么样呢? 稳定。 特征值必须是什么? [听不清] 对。 它将小于1 、或者如果它具有 Lyapunov 稳定、 它必须是 Equa LTO 1或更少该1。 是的。 系统是什么时候- 我刚才告诉过您。 离散 时间系统何时稳定 ISL? 还记得这是什么意思吗? 从 Lyapunov 的角度来看、它是稳定的 当 eigenvalue 剃须一个幅度时 大于或等于 1 因为实际上严格地说 是 Lyapunov 稳定性 还包括渐近 稳定性。 我们如何确定 给定的状态空间 是否在工作。 我为您提供了两种方法。 第一种甲基甲基甲 基甲基甲基甲基甲基甲基胺 模式分解。 我们对铁蛋白模式分解有何看法? [听不清] 是的。 是的。 模型输出 Matri x 中没有0列。 模式输出矩阵的每个列、 它们是伽马1、 伽马2、伽马3。 每个伽马耦合的对流二极管都朝向输出。 因此、只要这些 gammas 都不是0、 你知道所有 的表情都是通过耦合的。 因此 系统是可以观察到的。 还有一个测试。 [听不清] 是的。 您构建了 可观察性矩阵 Q 它是 C 转置、 转置、C 转置、 这些分区。 它应该具有 N 的全排名 观察性矩阵。 因此 、有两种不同的方法来确定它。 太棒了。 如何观察 可控制的规范表单 相关 我要找一个词。 双性。 它们是彼此的双重结构。 我 通过转置将系统矩阵相关联。 可见的系统 mmatrix、OCF 矩阵 是 CSF 系统矩阵的转置。 然后、您有 可控制的 B 矩阵 是 C 矩阵的转置、 观测 用例、反之亦然。 是的。 可观察性是 我一直在寻找的字。 我将为您提供该值。 QFN/SON 是什么? 它是什么? 它与 状态矢量的大小有关。 它只是 一个具有最小尺寸的系统 向量的 这就是它的样子、 换句话说、就是很大的尺寸。 与 FRAM 有什么不同?” 和 ARM™ [听不清] 是的。 那么、可检测性-是的。 我知道您的意思。 解决了可检测性问题 不稳定模式。 这意味着您可以 通过观察来检测不稳定性 输出端发生的情况。 现在、我们将 花一点时间吃午餐。 但在我们这么做之前 、我要感谢您 在 过去三小时内引起您的注意。 因为这是一项艰巨的工作。 它似乎很抽象。 其中许多是数学运算。 它看起来不像我 在做任何真正的事情。 但今天下午 、请回来。 因为我们 将获取这些信息 要控制双质量系统等系统、 飞行控制器等令人兴奋的东西。 我们以 非常真实的方式使用该信息。 所有这些东西对于 今天下午的到来都很重要。 因此 、对于那些从 TI 外部加入的引信、 我们在回退时看到了一些袋子 吃午餐。 我们将 在1点处恢复、 请重写 第7章。
线性系统的属性 、那么我们的介绍 熟悉 我们的房地产空间配方、 以及我们如何从中提取认证 信息、 包括矢量 和矢量值、 然后是动态 响应 之间的连接时, 优先考虑 MOSFET 表示法和 transfe 函数表示法。 该段 会进一步变小、 并检查 状态空间公式的属性。 尤其是、 非常重要、还有几个 想象 不到的其他人。 最不可避免的属性 是稳定性。 您可能会看到非常清晰的图像 我所说的稳定性。 很明显 、对于稳定的系统、 对于连续时间系统 、甚至是传递函数 稳定意味着什么。 您在看到它时就知道它。 它要么 是一个细长的 gthat 仍然绑定、 或者它不 会重新绑定、这很好。 但对于 stat 空间描述 其中我们有一 个内部变量、 稳定性分为几个级别 认知很重要。 当您进一步讲德语时、 如果您继续了解双头螺栓 非线性系统、 你会发现稳定性确实 是一个非常可怕的概念。 有这样的系统 外观 就像它们是稳定的、 看起来就像它们一样 同时在重写。 因此,我需要从 国家的角度解释稳定 空间说明, 特别是从状态开始 CEO 观点 然后,还有交流损耗。 这些是对资产空间描述的唯一性。 这些称为可控 性和可观察性。 它们不适用于 etransfer 函数描述。 但它们确实适用于 空间描述。 它们非常重要。 因为当我们稍后使用 进行设计控制系统时 状态空间模式、即系统 无法控制、 我们的努力将是徒劳的。 稍后 、当我们开始设计时 估算器或观测器 、这是相同的、 如果无法 观察到我们开始使用的系统、 同样,我们的努力 也是徒劳的。 我们无法从 无法观察到的系统估算 estat。 控制能力 和可观察性 是 我们稍后需要的重要属性。 现在、事实证明、稳定性 以及可控性 和可观察性、 所有这三项 如果 我们可以执行、就会有非常清晰的可视化效果 特定的近亲 DOF 变换 在系统上调用 da 模式分解。 我将向您解释 一下实际的模式分解 方法。 但是、如果您可以执行 eout、则会执行所有这些属性 您会非常清楚、 并且有好处 也是如此。 因此、我们将从 模态分解开始、 我将向您展示 所介绍的属性 以及 其他方面的术语。 然后 、我们将再次查看标准化的实现。 我向您展示了一 种、phas 可变规范形式。 事实证明、它 是另外两个被称为的位 可控制的规范形式 和可观察到的规范 因为此处是三角波形。 这就是为什么这个部分 恰好出现在那个部分之后 控制 能力和可观察性。 然后 是我要做的最后一件事 这 是一个 fairl yshort 部分、 最后要介绍的是冲头 下一个教程、我 将会或多或少地 每个教程都 将基于该教程。 它是一个双质量系统。 它由一 个有两个质量的机械系统组成 耦合在一起、 这样当你推动 水体时、其他质量就会移动。 但 两者之间存在某种能量交换 质量。 结果是振荡。 这是一个很好的、易于视觉化的系统。 它具有很多动态特性 让这些教程 变得有趣 这三种运动。 所以,我要启用系统。 驱动 ZVS 转换。 现在、我想先 解释一下这个概念 矩阵。 当矩阵使用 dfor 变换时、 您已经看到 、在 n 维度中、矩阵具有尺寸 n 乘以 n 矩阵为方形。 因此 、如果存在转换 在 三维空间中、从一个矢量到另一个矢量、 变换矩阵执行 三维变换。 例如、在这里 、我们有一个矢量 V、 它不由矩阵 T1运行 将矢量 t oa 变换为不同的矢量 V tilde。 因此、V tilde 是指向 不同方向的点 Gin 因为 它是由矩阵 T1进行操作的。 现在、T1、如 Wel las V 和 V tilde、 将以该坐标系的项 s表示 或者二者都是复数。 例如 x1、 y1和 z1、它们 可能是正交坐标 它代表矢量 和变换 权衡关系。 现在、让我们想象一下 、我们什么都不会改变、 但所有 这些信息都是坐标系 演示。 我们不使用 x1、y1、z1、而是使用 x2、y2、 Z2. 嗯,现在,相同的 tw omatrics-相同 的两个矢量 具有 slightl ydifferent 表示法。 因为它们的元件 将会不同。 因为它们 虽然指向相同的方向 从理论上讲、它们 在中重新呈现 不同的坐标系。 以及变压器 矩阵 从 V 移动到 V tilde、 这也会有所不同。 因为它的协调 帧发生了变化。 它在做的是相同 的事情、 但它是在 adifferent 坐标系中执行它的。 矩阵 T1和 T2 试用相似的矩阵。 它们可以实现 相同的变换、 但它们在 adifferent 坐标系中执行它。 它们与 所谓的旅游相关 相似性变换。 具体而言、T2 i 序列到 M、再到-1、 T1乘以 M、其中 M 是 相似性变换。 它将 Matri x 从一个坐标系变换 另一个坐标系。 且在 500 MHz 下,其 IP3 为 [听不清] dBm 时 不是吗? 您可以看到矩阵 M它必须进行测量。 它必须具有 与 T 相同的名称尺寸、 因为 T2的 esame 尺寸与 t1相同。 但是、当 你看到它时、M 乘以-1、 考虑相似性变换。 它将在 一秒内进入 com ein。 请注意,这是一个重要的属性, 那么、让我 花几分钟时间来讨论它、 难以仿真。 可以找到类似 的变换矩阵 M、它 采用 T1并使 T2对角线。 如果您可以 执行该操作、则会出现该情况 是 产生的许多好处 系统的电感。 该特定坐标系。 但 为了实现这一点、t1 必须具有一 组完整的特征。 否则、您可以 对 T2进行 tdiagonalize。 如果 T1没有一 组完整的特征向量、 您不能具有对角线 T2、 但您可以接近它。 出现的仿真形式、 称为 Jordan、用于 mrepresentation 稍后我会介绍。 但现在让我们想象一下,我们 已经不会有一整套特征的特征 这种 SoM 相似性变换可以实现 从而 使产生的 diagona lmatrix t2 该矩阵是对角线、bit 具有更进一步的属性 即您可以 对元素进行范围内的操作 对角线 Matri 的斜线、使其如此 以及系统的效率。 类似 的转变 这对你来说是一个 scolumns,它们本身就是这样 T1的特征向量。 这里有一些重要 的信息 一些特性。 如果 T1具有一 组完整的特征向量、 矢量 是定义的 CPU 独立 这些矢量 扫描用作列 以形成类似 的变换矩阵 M 因为 您知道、对于尺寸来说是可以的 你 有 n eigenvalue sin t1、t1是 n x n、 并且 您已经设置了完整值。 您有一个特征矢量。 每个特征都对 RHAS 中的元素感到羡慕。 因此、通过将这些列、 即 M、M 的列进行设置 尺寸也必须为 n b yn。 并通过使用 Matri x 实现相似性 变换、T2斜 线对角线、但不仅仅是 对角矩阵 T 1的特征值将是元素 对角线的对角线。 现在、在 我们了解该信息之前、 我 将向您介绍如何操作 您 可以使用状态方程进行状态变换。 现在、假设我 将一个状态方程式进行了打字 对于基于 关节状态选择的系统 影响。 我之前告诉过你 ,没有什么特别的 状态元素。 大家想用什么都可以。 那么、让我们假设 您做出一个选择、 它对 您来说并不是很有效、 您希望将它们更改为 不同的元素集。 没有理由不能这样做。 变化可能 会因所发生的事情而产生 称为状态变换。 那么、假设您使用的是 x 、并且您希望进行转换、 改用 v。 vis a different -- 我是说它是一个状态矢量、但 我现在将其称为 v。 它与 x 通过 这个矩阵 M 相关、即 现在是 n 的任意矩阵 那么、我们要做的是将 这个直接置于状态 等式、x 点等于 x plu SV。因此、左侧不是 x 点不再出现、但它是 M 时间 SV 点。V 点是新状态 等于 AMV。 MV 只是插入之前 的 xwas,加上 v 乘以 u. v 不变。 现在、我们要做的是 、我的 SWE 将对两侧进行预乘法 与 M 的倒数相反、如果 您可以的话、现在这是一件好事 M 由特征向量组成。 因为 M 肯定 会反向。 因此、您可以 从 M 中找到反向 它是正方形的、因此尺寸 是我们所需要的。 爬虫 程序会以 M 的倒数进行预乘、 您得到 v 点等于 m t othe -1、乘以 M 次 五、看,类似 的状态转变 矢量。 加 n 到-1 乘以 v 乘以 u 我们执行 了相似性变换 在电压矢量上的优先权。 并猜测 负1 AM 矩阵的 MTO 值 变为负数的区域。 它就是带宽。 它 将在前导代码中具有该 eeenvalues 对角矩阵 我们要将其命名为 LPO。 让我们将 M t othe -1B、B1称为。 现在、这是状态向量 Rinto 转换状态。 我们现在需要集中讨论 输出方程。 可以执行相同的操作。 但它要简单得多。 因为我们不会 将 ETO M 反转。我们需要的一切 将 x 替换为 M 时间 SV。我们将其称为 C1。 因此、C Time M 将 变为 t obe c1加 v 乘以 UD 不受所有这些影响。 那么、现在我们有了 stat 公式和输出 该 新状态的 I nterms、v、 v 恰好是多少。 现在、独特的选择 -那么、这里有 无限选择。 您可以随意选择名称。 因此、我们不会将任何 特定状态绑定在一起。 您可以在 一个和另一个之间切换频率。 但对于这种声波 ,v 的元素 有一个特定的名称。 它们被称为 系统的表情。 典型系统运行 I nCharacteristic Set of Patterns、 梯形脉冲。 这些模式称为模式。 它是 状态矢量的电子元素的唯一选择 这些称为模式。 这之所以很 重要的原因是 您将看到 每个模式的时间 与所有其他模式完全解耦。 这种变换、 独特的变换 其中您使用了 eigenvector 列的 Mmatrix 转换为-使用 我的 neffect 矢量变换。 这称为调制 分解。 在以后您了解到 自己可能希望 第一个是 、事实上这些模式是不耦合的 彼此之间、可 提供非常清晰的可视化效果 放大数模转换器和输出之间的信号。 不仅是这样、而且通路 从状态中的输入端 到输出 的状态要清晰得多 如果 你刚刚采取随机状态、你会更好 矢量 MAPS 动态特性 更易于解决。 因为存在 标量、而不是矢量。 您可以对 随时间变化的运动进行非常简单的视图、 它使 系统的动态变得更加清晰。 因为通过公开这些 值、 您知道哪些是主要模式、 这一点不太重要。 请记住 复平面中的电子滤波模式、 复数中左侧的特征值 比 那些衰减得多 在右侧、它们接近 虚轴、 如果它是一 个持续计时系统、那么它们就会被执行 与我 FIT 的离散时间系统并联。 您还可以 获得更清晰的见解 介绍了 tw 属性 更早的可控 性和可观察性。 我 认为通路暴露在外的原因 实现平衡。 该过程在 一段连续的时间内类似 奈奎斯特路径。 只是曲折 的特征值是不同的。 那么,让我们来执行它。 我们将编写 模态相似性变换 我 现在将其称为 W、 因为它是一 个非常具体的转换矩阵。 M、但 我想将其称为 W 由 列 sof W 组成 独立 的特征向量的特征向量 矩阵 A。因此您不需要 对列进行调整、 每列都有 n 个元素。 这是一个 n x n 矩阵。 我将为 该矢量添加符号 因为经济转型也是如此具体 以及 称为模式的独特选择。 我将为 符号 q 进行 E过渡期、 元素 wil lbe Q1到 q sub n 有 系统的模式。 是的。 就是这样。 现在 、存在 r表示 法变化 我想让您知道。 这是 EMI 滤波器部分。 这里是 输出端。 因为这 是一个独特的选择 的列数 W、正如我说过的、我们最终得到 了一个令人激动的新系统 矩阵 DMS 这是一个交流电机。 Lambda 将沿其前对角线包含 A 的特征 那么、写入这些方程 、Iguest 这就是它们的外观。 扇 出的模式矩阵包含在其列中 A 的特征向量 和频谱矩阵、 因为它称为 Lambda 、所以我对角线矩阵在这里 特征值位于 主对角线上、 所有的 释放都是零。 模态矩 阵 是应用 于这两者的名称。 现在、模式输入矩阵是 W 到-1乘以 v 我们将把 W 插入 状态变换公式 那个方程。 我已经解释过的 λ。 现在、输入矩阵 、W 至-1 v。当您 进行此分解时、 将 该输入的各个行分开很有用 矩阵。 因此、我一直将这些行 称为 sbeta 1、beta 2 至 β n 这些是 WTO 的负1 v 行,即 为什么我这么写。 可以将其视为变量。 但实际上 、它们是行矢量、 现在、输入矩阵的第行中有 n 个。 输入 矩阵的 Beta 1和 beta n ar ethe 行、 W 至-1 V 因此、这会 影响您的状态方程 看起来像完整格式。 左侧的模型矢量的导数 等于频谱矩乘 以模态矢量、加 然后、这些是 新模式输入矩阵的行 s. 但我想它们是 一个矢量乘以输入矢量。 如果您愿意、它 将为我提供测试版 捕获所有 电子输入到特定模式的耦合。 然后、Lambda 我捕获 从 Qi 到 Qi 点的动态。 那么、您现在看到了我的意思、即完成 去耦。 如果您可以用 此表单编写 estat 公式。 那么、这是模 态输入矩阵。 这就是它在 到达单个模式时的外观 您得到的方程。 那么、现在请注意 、这个 Lambda 我出现在这里、这是 是完全标量。 关键点是 动态不耦合。 输入矩阵。 现在、模式响应、之前 的每个状态派生 可能涉及 所有其他状态。 因为 状态矩阵可能有一个 da 行 它 一直具有非零元素。 但现在你得到的是我 只需一个一阶 差分方程、 涉及相同的模式。 其他模式不 会产生任何效果。 这是模式的分辨率。 因此、它是用来 修复瞬态响应的特征值。 这将为您提供 模式演进的增长或衰减。 然后、参与 积分涉及 β I 这样我们就可以 得到响应的整形 是 确定该值的矢量 通过 与 B.的关系 输出矩阵 I sthe 乘积为 C 和 W 这对我的想法很有帮助 作为 单独的向量。 此外,可能会发生击穿,这可能 因为该 wil 向上乘以向量。 因此、伽马1至 GAMM an、单独的矢量、 每个矢量对 成个单独的-一种单模式 所有输出上。 那么、这就是我 应该看到的样子。 我是说它们是向量 、但考虑它们 现在至少是标量。 正如我所说的、每个伽马我 都会闪烁一个特定的模式 所有输出上。 以便输出矢量 等于所有这些乘积的总和。 因此伽马1乘以 Q1、plu sgamma 2乘以 Q2、依此类推。 现在、我认为这个图 将把它全部绑在一起。 因为这是我们 所做的所有图形。 我们已更改了显示方式 完全 独立的套件 状态、每个状态 都是完全的 去耦所有其他的。 现在为 729。 因为 Qi 取决于 y 点、反之亦然。 以及空间与所有输入之间的耦合 由相应行的低确定、 输入矩阵的输出。 以及所有输出之间的耦合 由模态输出矩阵的 I colum n 决定。 那么、您现在可以看到吗? 您已经获得了非常清晰的可视化效果 所有输入 如何影响一种模式、 以及 MOD 如何影响所有输出。 这 种表示非常明显 发生的情况。 现在一切都正常、 前提是您已经完成了 一整套 eigenvectors。 如果您没有 、那么您可以使用的单向方法是这样的 如果您使用 了树形特征值。 那么、在我向 您介绍如何操作之前 您使用这些 信息来描述 我 想要的属性 o fa 系统 简单地轻触一下 、如果您有问题、会出现什么问题 有一个去生成系统矩阵。 它只能通过 反复的特征值来实现。 即使这样、我 也可能不会发生。 你可能会幸运 、可以说、你已经成功了 才会出现退化。 但您仍然有 一组完整的特征矢量。 或者您可能运气不好 、丢失一个或多个 铜。 因此、系统会发生退化。 当您遇到 eigenvectors 时、您必须 如果您要执行 TA 模式分解、 您必须 替换 mby、替换缺失的 具有 被调用的矢量的矢量 广义特征向量。 这些 仍将是真正的特征矢量的正交。 但它们不会 满足矢量的要求 我 在前面展示的公式、它是什么 是负 λ i、乘以 WI。 我们寻求 了一种微不足道的解决方案。 因此、它们会对 特征去变体进行泛化。 您可以在网站上找到这些信息。 有一个很长的 yprocess 可以找到它们、 我不打算 在今天的研讨会中讨论这些内容。 但一旦找到 了它们、您就可以使用它们 实现平衡。 但频谱矩阵、对 角线 eigenvalues 不再 是真正的对角线。 它 将在斜升对角线中有一些元件、即1。 这意味着电 极二极管不会完美 去耦所有其他的。 将会有一个小的耦合 EBIT 开启。 Matxri 的形式 具有该对角线、 但某些受支持 的对角线等于1。 它们称为 Jordan 矩阵。 矩阵、即 生成的系统矩阵、 或频谱矩阵、其中 有 Jordan 块。 现在 、在时会出现可能的差分排列 您开始丢失矩阵。 但从根本上说 、特征检测器的编号是 实现的最大值 取决于您 的解决方案 获取公式 A minu si 乘以 λ i 再乘以 WI α1α2 = 0。 这就是你发现了这些嫉妒者的方式,你还记得。 你这样做是为 lambda i 的选择 现在、我的 λ 一定 是可耻的、您可能会失去解决方案。 您可能没有完全 独立的解决方案。 您得到的数字取决于 在空空间维度 o fthis matrix 上、A 减 I 次 λ I. 空的 spac eDimension 会告诉您 您 将要获取多少个电子矢量 该特定的 Lambda I. 在本例中、 有一个整数 我叫 calin ghi、告诉你 可用 特征向量的数量 放大器驱动电路。 且 numrbe 介于1、 你将始终得到 1、而 Mi 特定 特征值的多重性。 如果您幸运、您可以使用 GE TA 全套、在这种情况下 你已经得到 了完全不一般的东西。 我们无需担心。 但是 、如果您没有这么做、 嗯、如果 你只有一个、你 需要这些通用 的去 igenvalues、 最后得到完整 的 Jordan 表格展示。 如果 您具有介于1和多重性之间的 你最终 会看到 Jordan Blocks 出现。 频谱矩阵 x 中有特定的块 它们具有1的超级对角线。 但它们并非全部为1。 它们中有些被压入。 让我来向您展示 一个有关这方面的快速示例。 这可能是一 个 Jorda 挡块 与特定的值相关联 具有一定的多样性。 同谋 是数字 对角线上的元件数。 您可以看到 、所有元素都是0、 但这几个除外。 这称为 Jorda nblock 或 Jordan 矩阵。 因为这是唯一的矩阵。 例如 、这里是一个五阶系统、 它具有三个特征值。 这有两个主要目的。 我有两个在-2处 、两个在+ 3处。 这 是一个不稳定的系统、1位于-1。 那么、在这个 scase 中、会出现什么 是 针对负2处的 tw oeigenvalues、 有一个约旦集团 的 kof A。你看到了吗? 它位于对角线上、 因此特征值 XY 尺寸更小。 但我们 需要的广义的 eigenvecto 在那里放置了1。 然后 、对于3、还有相同的细 gg 一个 Jordan Block 出现 在 ghere、对角线上有3秒、 对角线中为1。 然后是单 个特征值 给了我们一个 与它相关联的嫉妒。 因此 、您会在右下角得到一个很好的-1 i 类似情况。 现在、我将执行 一个快速教程、 只是为了向您展示 如何使用模式分解。 一次、它不再是 这些降压转换器的基础。 当 我清除其他一切时、请与我保持联系。 在本例中、我们在教程6.1中 分解-- 我不知道我做了什么。 为此我 道歉、我按下了一些东西 我不应该把 它分解 组成模式。 那么、很显然、这是 一个三阶系统。 我不知道它 将是怎样表现的。 但它显然有两个输入。 因为输入 Matri x 中有两列。 因此、我们有三个状态、 我们有两个输入、 我们有单 输出、因为 输出矩阵 C 的形式。它有一行。 因此必须有一个输出。 它具有 thre ecolumns、因为我们 知道有三种状态。 输入矩阵为0 - 转换矩阵 很抱歉、是0。 它包含两个元素。 因为有两个输入。 它有一行、 因为有一个输出。 那么、让我们分解 成它的组成模式、 看看会发生什么情况。 那么、首先、我们 要做的就是 hthen 使用 与我相同的方法构建系统 之前在 MATLAB 中展示的。 在我们进行 模分解之前、 我将绘制其响应。 我们将看到其 响应变化 模式分解后。 首先、我 将要构建 阶跃响应 、并绘制三种模式。 现在问题是 、这里有两个输入。 那么、阶跃响应 、问题是-原因 它 有两个 Pste 输入。 因为当 您执行一个步骤时、MATLAB 会对 LDO 产生什么影响 具有两个输入的系统上的响应是 有两组结果。 一个是 施加到第一个输入的 ste、 而第二个保持为0。 另一组结果 、当第一组结果保持为0时、 第二个应用 了阶跃输入。 因此 、这里将会有状态图的 tw oset。 它将反映 状态的维度 由此产生的矢量、 状态矢量结果。 我们可以开始了。 仿真结果如下。 上图是 三种内部状态的演变 当我们有阶跃应用 程序 dto U1、U2保持为0时。 然后 、在这里的底部图中、反向是 这些是 随时间推移的状态解决方案 因为 U1保持恒定、 而 nu2施加了阶跃。 现在、我们要做的是 perfor ma 模式分解。 我们就是通过这种方法来连接它的。 此 CLC 只清除 工作区中的任何内容。 这使事情 对我们来说有点整洁。 然后、我 将再次执行 EIG 指令。 请记住、这是 从中提取的特征值。 但当您使用 这两者的结构时 电 容、电容和电容参数 将返回模态矩阵 W、 频谱矩阵 λ。 嗯 、键盘对 lambda 没有注意。 那么、我将使用大写的 L 这是两个矩阵 、n x n、3 x 3 在这种情况下、将返回这些值。 您为其提供系统 mmatrix a、而不是仅提供平衡 意味着不要平衡 特征检测器、 我的意思是,我只是把 电子贸易机会这样做。 没有关系。 现在 、你已经把 W 变为原来的值。你可以 在类似 的变换中使用它 提取模式输入 和模式输出矩阵。 请记住、模式输入 Matri xwas W 到-1乘以 B 因此、我们将反转 W、 并将其乘以 B 我是雅斯特- 嗯、 我将断开它。 因为我很感兴趣、所以我 将行视为向量。 稍后您会看到。 然后、模态 outpu tmatrix 为 C 乘以 W 然后 、OIS 将代表它们 作为电流 LSB。 我们来操作一下。 您将看到 A、B、C 和 D 消失、 我们最终获得 L 和 MIM 0和 D 我不知道为什么 w EDID 不会结束-好的。 好的。 因此、它所做的就是再次为 我提供 A、B、C 和 D。 但这点我 是作为频谱矩阵的点。 这是 以指数值的 gof 表示的 λ 实现平衡。 这就是 EN/UVLO 引脚。 很好。 我想知道为什么它会被转置。 这实际上是正确的形式。 我不得不思考 为什么它被转置了。 但这是 输入矩阵的巨大形式。 因为它有两列。 有两种方法。 然后,还有交流损耗。 因为 其中有三种状态。 然后是 outpu tmatrix、模态输出矩阵、 透射 性 nmatrix 仍然为0。 我们现在将 执行相同的操作 我们在 Carrie dout 模态分解之前做过。 我们将进行预设 、并绘制状态。 现在,这是问题所在。 对于这种特定的状态选择、 因为我们有一 个完整的对角化光谱矩阵、 我们现在必须具有完全去耦内部状态。 每个状态 都取决于其自身的状态。 因此、我们得到了等于 λ i 乘以 Qi 的 Qi。 它们耦合在一起。 它是第一 个 orde rdifferential 等式。 这里没有其他东西。 您从过去就知道 、一阶解决方案 差分均衡 呈指数级。 因此、当我们计算 并解决这些问题时 对于阶跃输入、我们应该找到 1减去指数衰减 代码。 我们得到的确实是这样。 那么、这些是状态 、以及它们现在是如何演变的 变化情况。 因为它们 彼此去耦。 您可能会看一下 并思考、嗯、好的。 他告诉我们。 那么、什么。 可能系统也发生了变化。 但我 的观点是、它只是这样 系统实际动态的状态变换 不变。 换言之、 整个系统 无论 我是否表示、行为都完全令人感到羞耻 使用 SoM 耳本选择的状态、 或这个特定的选择。 我将向您展示这一点。 现在,我要 做的是,我要 绘制原始系统。 Y1的图、这是 原始系统的输出。 第二个传感器已经成功连接。 好的、这 没什么特别有趣的。 这就是系统的行为方式。 现在、我在 这里的 GTO 中所做的是、 这是一回事。 我将绘制 该图 Y2的顶部、Y2 是发射 分解的输出。 我 希望、所有这些变化 是该图的颜色。 它应该从蓝色变为绿色、 因为它是同一个系统。 它只是国际 动力学 以不同的状态选择表示。 这就是调制 分解为我们所做的事情。 [INAUDIBLE]? 使用 GA 模式分解的主要原因 从 mthe 输入到输出的路径 更清晰。 该属性意味着 可控性的属性 和可观察性、 可预测性等 更容易实现可视化。 看到 GPIO。 没错,这是问题的关键。 因为它会引导我 了解接下来将要做的事情。 [INAUDIBLE]? 是的、这是可能的。 [INAUDIBLE]? 嗯、它会使 引脚感到它 可能会将注意力集中 在非主导模式。 因此、它可能在这方面有所帮助。 或者您是否希望 简化系统 通过减少它的 orde rof、它可能会对您有所帮助 做出该选择。 因此、我 需要在控制设计方面提供帮助的原因有很多。 [INAUDIBLE]? 是的,确实如此。 [INAUDIBLE]? 嗯、有点像。 对,很接近了。 但我想摆脱 超前和滞后的想法 补偿器、也 是根轨迹的除法器。 因为在 系统中-我昨天介绍过 其中我们使用 doutput 反馈、我们 必须 关闭闭环 特定线路上的极点称为 loci 的复平面。 我们 可以更改的唯一精简 gg 是增益、沿 这些轨迹移动轨迹。 状态反馈控制的一大优势 您可以在 复平面中任意选择您喜欢的任意值 放置极点。 您具有极大的灵活性 接近 的环形极点所在的位置。 您 正在使用的栅极、FAC 而 不仅仅是输出中的状态矢量 好处。 因此、我认为这有助于 推进这一决策过程 极点的选择。 现在、我 将稍后更多地使用该小数位。 但我想 在一段时间内继续保持 kabout 稳定性。 那么,有两种 类型的函数。 在 我们继续之前、我想告诉您、 并了解如何使用它们。 第一个问题是,我们 可能会立即这样做 视为稳定的系统。 这一制度占有 财产 称为渐近 cti 稳定性 这意味着它的状态 i nthe initial condition 随着 时间的无限变化、 将收敛于该 电子平衡点。 因此、这相当于一 个稳定节点或一个稳定焦点 在我 之前向您展示的相位纵向中。 因为这种状态 会跟随某种路径。 这是一个稳定的焦点、 最终会随着时间的推移而出现 它稳定地稳定 在平衡点。 它称为渐近稳定性。 对于什么、有一个字的 ydefinition 这意味着、就 可以在多大程度上取代初始条件而言、 它与 平衡点收敛的事实。 因此、具有 连续时间值的系统 小于0、或者 如果是 rdiscrete time eigenvalue 小于 1的模数、具有属性 渐近稳定性。 现在、在 本幻灯片中、我能不能 做一些看起来 很明显的事情 您很清楚、 这一点非常明显。 因为它稍后很重要。 在稳定状态下 、对于渐近稳定系统、 如果是连续时间、您 知道稳态是 由 T 等于0的 x 点定义。 这意味着 estat 不再改变。 它达到 了它的固件点。 那么这是稳态。 但请注意、如果它是 离散时间系统、 存在陷阱。 因为我 在稳定状态下的意思 是 nex tstate 没有不同 输入和现态。 状态 XK 加 1与 XK 相同。 因此、当你保持 稳定状态时 对于分立式系统 、重要的是 右侧 不再是0。 这将在 我们看设计时再次出现 控制 系统中的稳态的高电压基准。 但我想提醒 您注意这一点 一个重要的差异。 实际上 、这是唯一的一个 稳定部队的差异 时间和 离散时间系统之间的差异。 因此 、稳态定义存在差异。 但无论如何、我认为您 可能[听不清] 想象一下,“那是一 种很棒的稳定。 现在 存在某种稳定性、 它位于 phas 纵向图中 其中平衡 点被称为中心。 一般而言、我 称为 Lyapunov 稳定性。 Lyapuno v컈 뚨 所说的是 如果您将初始 状态从其平衡状态中移位 然后让它运行、 前提是您没有 让它从 该状态转得太远、 它将对 状态进行收敛、 也可能不会达到无穷大。 它可能会保持 在平衡的每一个特征中 不 会在比赛中到达它。 这是 一个系统示例 它具有复杂的共轭 值、如果它是连续的 时间、或单 个转盘上的电子值、如果它是离散时间。 因为这些振荡 是持续的。 它位于边界上、不稳定。 它称为预翘曲。 有时您会看到具有 Lyapunov 稳定性的系统、 被称为稳定的是 Lin 的 Lyapunov 感。 这不是我们担心 的事情。 但术语会不时出现 、尤其是 非 线性系统的应用。 但执行 此操作的系统、在本例中 它是二阶 的、它的相位纵向会是 属于 中心的类别、 它具有利亚普诺夫稳定性。 现在 、绘制了两个车床图 就输出而言, DPWM 模块 2 和 此电路的频率响应。 我将讨论的是、没有 WIS 如何涉及输入。 因为 输入的有效性允许 我们将在 内部和外部进行区分 稳定性 首先、 内部稳定性是 耦合的属性介于 输入和状态之间。 它有时称为边界 性状态稳定性、 或 BIBS 稳定性。 有时、它是回调 式内部稳定性。 因为我们在谈论内部 变量集 称为状态。 提供 RA 有界输入、 状态保持 受限 获得 BIBS 或内部稳定性。 如果您解决 稳定性的均衡问题 主动能量传输。 显然、您正在寻找 外部信号。 以及 外部稳定性 当有界输入仅 产生有界输出时定义。 您具有 BIBO 稳定性。 现在、因为输出均衡 仅是代数方程 涉及到状态、则会提供 有界输入 有界状态稳定性、您会 自动获得有界输入 宽输出稳定性 因为在 该状态下、动态特性仅在那里 但不会相反。 这并不一定是一 个关键问题、因为系统是这样的 外部稳定、 内部稳定。 要确定该值、 您需要确定 状态如何从 内部耦合到输出、 主动能量传输。 您可能具有内部状态、这些状态 会像疯狂的那样振荡、但 不会耦合振荡 到输出 电流、因为存在 是输出矩阵中的0个元素。 因此、内部 稳定性是肯定的 可保证外部稳定性 、但不会相反。 好的, 现在、让我们来了解 一下可控性 10K 欧姆的电阻器。 稳定性概念也 会进入这种情况。 我有她 的 eis 四阶 已 执行模式解调后的系统。 它与 我之前展示的图表类似。 因为每个 表情都是完全的 与所有其他组件不耦合。 输入和 每种模式之间的耦合 由 W 减1 B 矩阵的 sw 行确定、 以及从 EAC 模式到所有输出的耦合 C Wmatrix 的列、这些伽马元素。 现在、 这是 W 的异或响应行 负1 B、因此 Bi 转换器 是非零值和伽马 I 非零、很显然 、tmode 是通过耦合的。 因此、您可以说是 因为输入 耦合到该模式、 我可以影响该模式 来减少输入电压。 因此、我 所说的模式是可控的。 因为 CW 矩阵的相应 gcolumn 非零、当该 模式移动时、它是 某种程度上会影响 至少一个输出。 因此、这 种模式的情绪 观察到的相关事物。 模式1被认为是 可控制和可观察的。 您可以看到我 在这个图上进行了详细的了解。 因为您知道该 异或响应矢量、 Beta 1和 γ 1为非零。 现在想象 一下伽马2为零的位置。 这意味着该模式不 会耦合到输出。 我们无法 通过观察输出来确定 gSimply Q2是否稳定 EOR 为不稳定模式。 因此 无法观察到 tmode。 但由于 β 2是非零、 因此它与输入耦合。 因此我们可以对它施加影响。 这 是一种可控但无法观察的模式。 当 reverse 为 true 时、您可以 看看 模式3会发生什么情况、β 3是零、 但伽马3不为零。 因此、这种模式是不可控制的、 但至少可以观察到。 最后、有一种模式 、它与任何东西都是解耦的。 它是一 种无法控制的模式和一种无法观察的模式。 因此、这些属性 非常明确、 模式分解后、它将立即开始运行。 首先、 正如我说过的、它们的重要性是、 您无法确定 任何相关内容 内部可控性从 传输中循环伺服 功能描述 这些只是 状态空间描述中的属性。 幸运的是、物理 系统 控制 器和可观察的、 这意味着、当您 从头开始构建 astate 空间模型时、 某种系统、 即实际系统本身 那么这里的电压将大于 VOH。 但您的模型通常 包含一些简化 或一些假设、意味 着模型可能不会 具有这些属性。 因此您无法 控制 系统或观测器的型号 您的系统模型。 如果您选择的 stat edoes 具有这些属性、 然后执行 astate 变换 不会更改属性。 因此 、您使用的 wha tstate 选择无关紧要、 证明其正确性。 和可观察性 是系统独有的、 而不是选择状态。 你往往有各种原因使稳定部队有问题。 最常见的原因是您 忘记了有极点 在 您的转账职能部门、您可以在此处取消或取消预订 或 等效的传递函数 说明中有 偏斜极点和零点。 但由于 其他原因、您可能会运行 int oit、 例如、对状态进行明智的选择、 或可能是国家数量。 这些东西也可能会降低 可控性 简称 WCT。 首先是包络。 总结 一下左侧的两张幻灯片 sago IAR。 因为只是很喜欢 动态、 从 输入到模式的连接路径、 β 1和 β 2列矩阵矢量 为 SPI。 Q1和 Q2 与输入进行爬电耦合。 那么,这是一个 RAM 地址。 而系统在黄昏中是无法控制的 功能模式。 但它是具体的模式 2、这是不可控制的。 因为模式2未 连接到输入端。 Beta 2是一个0矢量。 这是 IC。 因为这个 特定的特征值 位于右半平面。 这意味着 系统不稳定、 无论如何、GWE 都无法做到这一点。 因为我们无法 控制不稳定模式的通量。 这种薄 的 gg 可能不是很明显 如果您只需要随机 选择状态变量、 以及完整的可变状态 器描述。 但 它可以避免雪的存在 系统中存在不稳定和不可控的仿真二极管。 这将在稍后引发问题。 因此,如果您 在这里有电阻, 分类是 可控和不可控的 非常清楚。 您只需查看 rnonzero beta i 矢量。 这 是一种查看事物的方法。 还有 一个代数测试 适用于一般情况。 代尔拜 ctest 就是这样的。 您首先必须构建 可控制性矩阵 从现在开始、我将调用 P可控性矩阵 这样。 现在、这是 calle da 分区矩阵。 我想这是 昨天的 Matri x代 数笔记中的内容。 一个分区 Matri xcontains 元素 它们本身就是矩阵。 eis 上的这个特定结构如下所示。 它是 B、A 乘以 B、A 平方 B、一直到 A 到 n 减1乘以 B。让我们细小 它的尺寸。 B、您知道、i n x r matrix。 它有 n 行和 r 列。 a 是方形矩阵。 因此它不会 改变行数 有很多类型。 AB 将 会进行仿真、因此是 n x r 矩阵。 A 平方 B、类似地、n 除以 r 因此每个 分区都是 n 乘以 r 因此 、整个东西中都有 n 列。 您有 n 行、您 有 n 次 r 列 一个示例。 然后、你所做的 是、你看一下它的排名。 现在、请记住 矩阵的侧面 是 最大非零决定因素的尺寸 任何位置。 那么 、对于这个矩阵、你可以得到的最重要的排名是什么? 你不能大于 n 因为它中有 n 行。 它有 n 乘以 r 列。 那么、您有一个输入。 它将 是 bEAN n x n matrix。 这就是 EMC 问题。 如果您有10个输入、它 将是10n 的10倍。 但它不能得到大于 n 的 bigge、因为你 需要一个方形 Matri xto 具有一个决定因素。 因此、你 可以拥有的最大的 RAN 是 n 现在、如果这个特定 矩阵具有秩 n、 系统是可控的。 您是怎么做的。 对于离散时间系统 也可以这样做, 唯一的区别是 电位变化、A 的 C、 B 的伽马。 否则、您将构建 控制 器矩阵、并对其进行评估 完全相同的方式。 您 可以说有 SoM 的表达方式。 如果您只有一个级别 o fv、其中 v 小于 n 然后您知道您 只能使用 v 可控模式。 您有 n minu SV 不可控模式。 因为其中 n 减 v Beta 检测器为零。 还有一些人在可 控制性指数中进行了定义 因为 它是必须具有的最小数量的分区 添加、直到您获得全排名。 嗯、无论如何、这是第三 个可控制性指数。 现在、可观察性非常 相似、令人惊讶的是、 令人震惊的相似之处。 我有一个问题。 请说。 [INAUDIBLE]? 是的。 [INAUDIBLE]? 当然。 [INAUDIBLE]? 好的。 [INAUDIBLE]? 你会说 滴滴不会改变。 它 将永远到达一零。 你们得到的是这个吗? 是的。 就是这个[听不清]。 它将如何激发? 是的。 答案 是、我在数学上讲这个东西 将永远保持为零。 实际上,我们没有这样做过。 存在影响 系统的噪声和扰动 实际上、您只是 不知道。 它不会保持为零。 但你已经确定了你 不能影响它的 FAC 低电压。 因此、无论发生什么 情况、您都无法更改。 什么都不会改变。 因为会 有激发它的 SoM e扰动。 然后实习 YIT 将会增长。 但从数学角度讲、您是对的。 没有什么可以激发它的。 因此、理论上、它 永远不会保持为零。 但这不是必需的。 是的。 这是 ROM。 音频正常吗? 是的。 好的。 因此、继续 观察、 没什么特别的。 我们解决 了可观察性的均衡问题 放大数模转换器和输出之间的信号。 它是 CW 矩阵的列 s 它为我们提供该信息。 如果它们都是非零、 那么-即使是模式 通过输出耦合。 因为 γ 1、即 refxample、决定了 Q1与 所有输出耦合的方式。 在左侧、有 一个可观察的系统。 它仍然是一个不稳定的系统。 因为如果 N 大于 0, 它是一种 弱实时系统。 大家可以看到这一点。 因此、该电子模块 将会振荡。 但至少我们可以检测 输出端的振荡。 这是 可观察性的定义。 右侧是 I hav EAN 不稳定系统。 我认为它具有相同的模式 、因此具有相同的特征值。 但这是不可观察的、 因为伽马2是0。 CW 矩阵的第二列为0、 因此、secon dmode 未连接 任何输出。 我们 没有什么可以检测到什么 第二种模式将会执行。 这 也有一个代尔拜克特尔。 它涉及形成 顶点矩阵 时间反转函数。从现在起、P Q 将为 这两个矩阵保留 dd。 因为我们现在非常需要 GTO。 现在形成 了分区 从 C 转置、转置、 转置、转置 转置等。 您在 该矩阵中查找运行 kof n。 如果您有它、 则可以观察到 nthe 系统。 如果您没有 该系统、则无法观察到系统。 离散时间有一个并行 替换为 C 的系统 现在有两 个相关的附加属性。 其中第一个是 我的扇贝稳定性。 IO_SUP 与 RX_SUP 相同。 但问题是仅针对 不稳定模式。 我来举一个例子。 这是一个系统、它是 一个无法控制的系统。 因为我们知道 FIRS tmode 与输入不耦合。 因为 Beta 1为0。 因此、这个 modeCAN 执行它所需要的任何操作。 w eCAN 无法影响这个模式。 但它是一种稳定模式、 至少它是稳定的。 但是、第二种模式是不稳定的。 但它具有一 个非 Zer obeta 2矢量。 因此、它通过 输入耦合、 因此、w eCAN 会影响它。 我们可以稳定 输入的 b y 操作。 因此、我 可以控制该系统、 需要的电压电平。 但至少它是可以稳定的。 但可以设计它。 还有另一 个与此相同的 mter。 但它会应用于输出。 它称为预翘曲。 它是可观察的、但只能寻址 到不稳定的模式。 实际上、它是 Sam esystem、 但在这里、您已经获取 tgamma 1非零值、 第一种模式是耦 合到输出。 第二个问题是可靠性。 现在、这里的第一 种模式是不稳定的。 因此、它 是一个可检测的系统、 降压-升压解决方案的大门。 第二项要求源于 虽然它不可观察、 因为它是稳定的 则可以说器件具有 ELDRS。 这意味着、如果 涉及到一个 yinternal 振荡、 系统内部任何不稳定的东西、 至少您可以检测到它。 因此、我通过 两种方式定义了可控性和可观察性。 我已经定义了稳定性 和可检测性 是可控 性和可观察性 但仅解决 不稳定模式的问题。 下面我们快速测验一下。 因为这 真的很有趣。 我们将对 结构特性进行调查 四阶系统的性能。 我 没有任何 IDE。 因为我不记得 本教程是如何实现的。 那么,让我们看看两种情形。 首先 、我们创建系统。 这里没有 什么令人惊讶的东西、 仅使用 SS 和 A、B、C、 D首先、我们要介绍 进行稳定性分析。 现在 、MATLAB 中有一个手录。 您不必担心 像 eigenvectors 这样的事情 和特征值、以及在 左半部分计划中的工作情况、 或右半平面。 您只需键入即可保持稳定。 是稳定的、它真的需要所有的东西 、不是吗? 因此、 您所做的是、您键入的是稳定的、 或者它是稳定还是不稳定。 是的。显然这 是一个不稳定的系统。 我们还不知道它。 但它是一种电路外的 EOS。 现在、我们要在 GTO 中做的下一件事是检查可控性。 我首先要做 的是我正在看 显示了片上 SRAM 的大小。 这将告诉你维特 尼-现在如果你在这里键入1、 它将告诉您 行数。 如果您键入2、则 会显示列数。 因为 它们的尺寸为1、2。 但我知道 AIS 是一个方形矩阵。 因此、这并不重要。 这将告诉我 系统的尺寸是多少。 当然、在 本例中、它是4。 然后、在这里、我 介绍了重要的一行、 因为这是 可控制性矩阵的构造。 CTRB 构造 控制性矩阵 您 所需的两个抹香 为其提供 系统矩阵 A、 和输入矩阵 C 因此,我们 现在对 P 退了 我只需要了解 P 的级别 与 A 的尺寸相同、它 是系统的等级 和系统的尺寸。 如果是、 则系统是可控的。 如果不 是、则是无法控制的。 很高兴这 是一个可控制系统。 因此 、在那里的某个地方有一个不稳定的仿真二极管。 但至少它是可控的。 因此、您可以说 该系统是可稳定的、 尽管它不稳定。 现在、我们将为 可观察性做类似的事情。 我将使用构建 可观察性矩阵 Q 为其提供 A 和 C 矩阵、 然后再次检查排名。 希望运行 的 kwill 等于4。 不幸的是、它不是。 等级小于4。 因此 、系统无法观察到。 并尝试 去探索神秘之地 在这个系统的后面、我们 将进行模式分解 你会发现这是为什么。 那么、我们将 共同定义 A 的 EIG 为我们提供一 个模态 d光谱 矩阵、 然后计算调制 线性输出和输出矩阵。 这是下一个脚本中的目标。 我们可以开始了。 现在、在我们 进一步讨论这个问题之前、 一些属性 现在变得清晰。 因为我们所做的都不 是模态分解。 我们显然拥有 完整的一组特征值、 和完整的特征 矢量。 由于所有 这些值都不同、 因此,我们知道我们 不会成为一整套特征的特征。 但是、如果您看 一下它们、左半平面、 左半平面 、你得到的是加1。 这就是 系统不稳定的原因。 这里有一种积极的价值。 3号为正。 嗯、我们知道它是 一个可控系统、 所以 我们不应该感到惊讶 einput 矩阵的所有行都不为零。 但我们也知道我 无法观察到、 这意味着 模式的 SoM eof 不是 噪声有多少。 输出 矩阵的头两列 为0。 因此伽马1和 伽马2都是0。 但伽马3和 伽马4不是0。 我们已准备好 [? 我们有 ISO-21848。 我们有 ISO-21848。 现在、 我告诉过您的其他一些属性 稳定性 和可检测性。 那么、让我们 先处理稳定性问题。 这 是不可扩展的系统吗? 是的。 米歇尔说是的。 每个人都能实现 经济转型的稳定? 它是稳定的、 因为所有模式都是如此 RTI = 参考了输入 因此 、无论模式的音调如何都是不稳定的。 它通过耦合。 因此它 可以稳定下来。 这是可检测系统吗? 为什么没有呢? 好。 嗯,请思考一下。 可检测性是可观察性、 但仅解决此问题 ECG 波形总是延迟。 因此、我们不是处于 稳定模式的中间位置 不稳定的情况。 嗯、它是第三个 不稳定的模块。 因此、我们将提高 可检测性、 可观察性。 我们需要 CW 矩阵非零的第三个色谱。 就是这里。 通过观察 gthe 输出、我们得到了 至少得到 了这个东西的电子信息 变为负数的区域。 这 是一个稳定的电子和一个可检测的系统。 但这并不理想。 这是无法观察到的 、整体来看。 因此 、该系统具有这些属性。 好。 我希望我们几乎就在那里。 我们有两种形式。 我不打算对这个进行人工操作。 因为我已经完成了。 这几乎是午餐时间。 这是 phas 可规避的规范形式。 这两者之间的任何不同之处 我 在上一张幻灯片中展示了相位 变量规范对于 mon、它是标题。 它称为控制 器 ecanonical 表单。 您可以通过 我向您展示的过程来实现这一点 开始, 您会得到矩阵的非常识别的电子结构。 您可以从 系统矩阵中获取该值 其中所有 的不祥因子系数 显示在底部行中。 除 超对角线外、矩阵的其余部分为0、 即1。 这是因为状态的选择、 即状态选择 是相位。 B 矩阵、输入矩阵 、为0、除了最后一个矩阵。 C 矩阵、 输出矩阵、 包含 分子的系数。 当您看到它时 、您就知道您是 处理控制 器 ecanonical 表单。 它称为自动生成该表单 可控 今天 下午、我们将使用这种形式 设计状态空间系统。 现在 、有一个类似的形式、称为 可观察的规范形式。 我将 很快地向您介绍、 告诉你 滴滴的关系非常密切 与可控 性表单非常接近。 该矩阵是 可观察到的规范形式、 现在我将调用 OCF。 好。 您有 CCF 和 OCF、 您可以看到这些缩写。 OCF 系统矩阵 与 CCF 系统矩阵相关 锁存器。 这就是所有的不同之处。 现在来看看关断, 对于观测 表例形式、 输出为 经济过渡期 控制 器规范形式的矩阵、 这两者也与 转置相关。 在某种意义上、可 控制的输出矩阵 是 可观察输入矩阵的转置、 反之亦然。 接下来,请看这里的 观测 表例形式的矩阵、 它与输入矩阵相同 可控制的 canonica lform、只是转置。 因此、如果您了解 一下音调描述、 您已经自动 获得了另一个、 如果您现在有 转置、OCF 和 CCF。 现在、 当我们来到这里时、这些东西令人非常愉快 进行状态空间设计。 CCF 更改了状态 反馈的设计 非常简单。 和 OCF 表格让 观察员设计人员 简单的提示。 现在它们是 calle dcomp配套 表单。 它们通过 这些转置相互关联、 我在 上一张幻灯片中向您介绍的内容。 但是、这种关系我 非常强大、 您最初可能想象的更强大的功能。 这种关系的名称 称为 duality、 这意味着这两个系统 被这些矩阵所描述 相反的信号线。 因此、您可以选择 其中一个的可控性 检测 对方的可观察性、反之亦然。 因为如果您在寻找 P 和 Q 矩阵、 它们的关联 方式与我的关联方式不完全相同。 请记住、P 矩阵是 B 分区 B、A 乘以 B、 乘以 B 可观察性矩阵 I twas C 转置在 B 位置、 和 A 的转置 I nplace。否则 完全相同。 因此、当您检查 其中一个的可控性时、 您实际上正在检查 另一个是否具有可循环性。 这种类似的并行功能有助于我们以后的工作 详述这一点。 因为使用 的技术是这样的 电压反馈控制器的设计 与 您用于观测器设计的完全相同。 这是一件充满力量的事情。 因为您只 能获得一组流程、 您可以执行这两个作业。 在这一部分的最后, 我 将向您展示一个非常简短的教程 可能会出现什么问题。 有一个术语"最低 限度实现" 这意味着您找到 了具有最小空间矢量的空间矢量 可能的尺寸。 以及您的模型可以使用的 GIS 的功能 在那里有状态、什么 都不做。 保存的操作太多。 您可能有 第三阶系统。 但你不小心 给了它四个状态。 当你这样做的时候 ,事情可能会出错。 通常 会出现问题的是您 失去 了我刚才讨论过的一个属性。 例如、您会丢失 可控制性属性、 这意味着 UCA 无法控制系统。 因此、您必须开始 确保已经完成了 具有可控性。 如果没有、请看一下。 您是否在处理 实现问题? 为了说明这一点、 我将执行它 以组织形式提供、教程6.3。 这意味着、对 可控性和进行调查 三 阶的可观察性属性似乎无害 一个输入。 因为 B 矩阵是 acolumn 矩阵、并且有一个输出、 因为 C Matri 坐标轴是行矩阵。 那么、让我们在 MATLAB 中查看这一点、看看会发生什么情况。 因此 、从一开始就没有什么令人惊讶的、 我们将开始 建立这一制度。 命令窗口中没有任何显示。 但这些是 工作区中的 Matrice swover。 我们已经构建了系统。 现在、我们将确定 首先可控性、 使用过去 用过的技术, 构建 可控制性矩阵、 并确定其等级是否为 等于 系统矩阵的大小。 如果是、 则系统是可控的。 如果它不 是-嗯、它是不可控制的。 但令人高兴的是、这是一个。 因为系统 mmatrix 是3 x 3。 这是 P 矩阵。 我们正在寻找它 中的大非零决定因素。 实际上、它会发生 这种情况 具有非零决定因素。 因此 、该矩阵的排名为3、3等于3。 因此、这 是一个可控系统。 现在、让我们继续、为 可观察性做些令人遗憾的事情。 我们已经知道 n 是3。 我们不必重新计算它。 可观察性、这 是可观察性矩阵。 不幸的是、最大 非零决定因素是2 降低了 2 毫瓦。 在这里、它具有2级。 2小于3、这 是一个无法观察到的系统。 现在、为了找出 原因、我接下来要做的是什么 查看 传递函数的 stat 部分。 因此、我将 使用脚本转换 S STO TS 要转换为 transfe 函数描述、 然后 TS 从 它构造 G、即 etransfer 函数。 我们来看看这个。 简单地说、好的、 到目前为止没有什么明显的。 它是一个三阶系统 、其中包含两个零。 现在、我们接下来要做的是、I SWE 将使用此 ZTK 脚本。 请记住、这是 一个显示极点和零点的函数 信息作为数组。 因此、这将告诉我们 分子是什么 分母是相同的。 这将显示 极点和零点。 此时、您 可以看到存在问题。 因为 这里有一个阻抗极点。 一个极点位于 S 等于 sminus 1、另一个零点 时间极点开始。 据说这 是一种微不足道的认识。 现在、我在这里看到 一个 TA 相当简单的系统。 系统会变得更 复杂、 订单数量众多。 找到这些东西有点难。 有时您不需要 转至传递函数 以查找它们。 但很高兴 MATLAB 为您提供 了一个名为 minreal 的脚本。 看到、 MATLAB 花费多少钱-花费多少钱是惊人的 MATLAB 工作将从它中取出。 MinReal、您将为我提供 传递函数。 在本例中、G1是 ZTK 形式、然后是 将返回 rtransfer 函数、 控制器,即这里的 EC。 在本例中、它将为 我们移除该消除极点。 现在、我们有 一个二阶的 transfe 函数。 我可以继续 对状态空间进行疏浚 评估它的稳态响应。 现在、我 在做它的方式、你会的 这也是一件事 、就是回来 这些系数数组进行比较 该设计的链接。 这与该 TS 数据不相关。 它返回枚 举符和分母的数组、 将系数转换为数组。 然后使用 TF 到 F STO 返回另一个方向。 将函数 转移到状态空间、 它将这两个数组作为 对四个矩阵的返回值 空间描述中所需的所有信息。 我们可以开始了。 现在有 了秒序系统 以国家空间形式表示、 这是一种最小的实现方式。 最后一件 行李简单地确认了 我们现在处理 的是可控和可观察的 转换器。 它与 之前应用的测试 SWE 相同、 构建可控 性和可观察性矩阵、 并在 本例中检查它们的侧面是否为2。 因为 系统的顺序减少了1。 我们可以开始了。 2是 系统的 orde r. 我们有一个2 x 2矩阵、其等级为2。 这是可 控制性矩阵。 因此、我们仍然很好。 现在是可观察的 Matri 坐标轴2 x 2、它有一个秩。 现在、我们也开始 了可观察性。 因此您可能会遇到问题。 这些问题往往 会降低可控性 简称 WCT。 因此 、我们在本次课程中几乎没有遇到过这种情况。 然后、我们将 准时地点餐。 现在、我要在 GTO 中使用的系统非常一致 今天下午 、对于教程、 是一个机械系统。 它基于像 这个这样的双重 sma 系统、其中 有两个质量、M 1和 M2、它们在坐着 并在 某种情况下自由滑动。 因此、您可以想象 这两个质量 金属块或桌子上的某种薄格。 我们可以影响 他们的立场 从 质量 M1的黄昏开始。 当我们这么做时、 很显然 M1将移动。 其位置称为 Y1。 当它移动时、它会 在 M2上施加力、 因为它通过 该弹簧减振器与它耦合 组件 现在、这些 sprin gand 风门值 耦合的情况 耦合非常轻微潮湿。 这意味着、当你在 M1上给它一点细微差别时、 M2将 像这样进行归零、 它将在很 长一段时间内继续执行 lik ethat。 因为 那里有非常轻的阻尼。 那么、现在、如果我构造 它的 da 模型、 就像这样、这可能 会永远地滑动。 因为 没有什么东西可以阻止它。 我所做的是、我已经对 DIN 进行了几个摩擦术语的说明 因此、我 当然不会 你知道 会有摩擦。 这种化石 正在发展 死机有两个原因。 一个是 因为它有点潮湿、 另一个原因是 存在滑动摩擦 这 将最终在这两个质量中获得成功 为了平稳的停止、我 只需给它一个踢。 现在、我 想变量 o finterest 是 Y2。 我想我 在这里的工作就是我 力控制、 施加到 M1的力、 希望专家组 Y2 在我希望的位置。 当然、在 不受控制的无反馈中 情况、某种程度的操作 计、实际上是死算。 但 您将在今天下午晚些时候看到 Ron 控制的应用、 它是令人惊叹的超精确度 使用 gof M2的位置、即使有 它们 之间的间接耦合、 它们之间的轻微阻隔耦合。 现在 、我选择它的原因是 您可以将 此处发生的情况可视化。 它 有一个很好的统计器空间描述。 我将此作为新 版本的书中的附录。 它还可以从 网站下载 附录。 因此、如果 您访问网站和您 查找 该书的版本、 如果您不 想购买这本书、 您实际上可以在 此处重新创建附录、 附录 E、它实际上为 您编写了所有这些内容。 这是 PDF 格式的电子附录、 欢迎 您下载。 而不进行详细 介绍 是运动方程。 这就是这个空间方程的样子。 这是二阶的。 您有 一个4x4系统矩阵。 什么 情况下发生呢? 太好了! [INAUDIBLE]? 抱歉。 您在附录中给出了它。 这里有一些 mor 电子信息。 我能不能事后跟你谈谈这件事吗? 因为我没有 完整的推导 而设计。 这将有所帮助。 是的,可行。 是的。 我可能应该这么做。 我还没有完成 整个推导过程 而设计。 但方程 中的"sher"几乎是正确的。 它们 不是完全正确的原因就是这样。 我也可以告诉您。 看到、我刚刚应用 了牛顿的第二定律 以获取这两项。 这里也有一个摩擦力。 因为这是 关于运动的电子方程 第一个质量的值、其为 输入力 u 其中涉及的内容。 我已经将 状态指定为 第一 块块块块块块块块的位置及其导数。 那么、这是第一 个质量的速度 DOF、 以及 secon dmass 的位置及其导数。 因此、当我为 x2点形成电子方程时、 乘以加速 因子 nx2点等于所有该批次。 问题是 这里的 mas sterm 出现在左侧。 因此、您将会遵守 这些其他条款 乘 以 M1除以除法、 左 侧有 x2点、如果您愿意、 控制器,即这里的 EC。 而薄 的 gthat 出错了 我忘记 了将该项除以 M1。 那么、在 这里的方程上、这不应该是1。 这应该是1除以 M1、对吧? 因此、无论如何、我在 六个月前发布了该内容。 我了解 了这种情况的结果。 因为有 七或八个像 附录 E 中的不同部分和所有拓扑。 我们的到来 非常漂亮。 然后我开始了 BAC KTO 在我发布了 Dar ning 之后、我查看了它。 天哪! 我忘记了 M1。 您知道 我为什么要离开它? 因为 M1是1千克。 因此 、我在人生中有一次很幸运。 因此 M1是1千克。 好。 现在、让我们快速 学习本教程、 您将看到该 系统的行为、 或没有行为、具体取决于 您的行为定义。 好的, 好了。 所以、我们要做的 是非常精细的非常细化的 gery。 我已在脚本中更正了它。 在这里、我们将使用 SS 函数创建模式焊盘 以创建状态空间模型。 就是这个。 现在、我要做的是 执行模式分解 就像 我之前所做的那样。 我们将看到 模体的外观。 现在、它是一个拥有 一整套特征器的系统。 因为我 现在有一个完整的对角线模式矩阵。 但您已经可以使用 这两个特征值 非常复杂。 因为大多数 esmall 实际组件、 但想象中的分量 非常虚幻。 因此 、您在这里有一个较低的振荡。 我们可以 从中看到的 在第三种模式下存在一个非常小的数字。 这可能意味 着系统不稳定。 但这并不理想。 这低至 MATLAB 的分子分辨率。 这是一个0 eigenvalue。 我们有一 个模式线性输入矩阵 它包含一组复杂的术语。 因此、我 可以控制系统、这很好。 您可能会想象 它是什么样的系统。 和模型 outpu tmatrix 类似 一个复杂的术语集。 因此、它也是 一个不可伺服系统。 到目前为止一切顺利。 我们可以像 以前一样,以同样的方式来核实这一点。 那么、让我来证明 它是可控的 它很复杂。 现在、我要做的是 不执行初始条件 评估它的稳态响应。 我将从 x 矢量中转到 t*、它 因为这里有 四种状态。 我将从 该状态中提取第一状态和第三状态。 现在、我已经在其中添加 了这两者之间的初始分色。 因此、这个 y0 更远、 这表示初始 化两个质量 被距离隔开。 我想我使用 大约一个仪表。 它是一 个非常好的双系统、这个。 那么、当我将其添加到该位置、 然后减去第一个 从第三种模式 中、我从 Y2减去 Y1、 并添加初 始偏移。 因此、这将为 LME 分色 质量的影响。 当我运行它时、 您会看到 EIT 是一个振荡系统 确实。 这是一个曲线。 但您将 看到它会下降 我们开始控制它。 总数值非常高。 因为你给了我 一个微移、它将会运行 就像那样。 这就是 EN/UVLO 引脚。 让我 第二次运行 BAC KA、然后向您展示 我使用了什么初始条件。 这个矢量、我在这里 对第一个位置质量进行了调节 稍微偏右一点、 这是一个正向。 第二个是 左侧的易碎位。 因此、我稍微压缩了一下 sprin GA、 然后放开。 因此、这 种平装的东西压缩了它 为 10 伏或类似的电压, 它会停止所有该运动。 这是 IC。 现在、我们将绘制 单个质量位置。 这是 所涉及的绝对的排列。 因为我 将 Y2的开始考虑在内。 Y0被添加到 Y2中。 在 我们应用该测试时、您将看到行为是如何的。 好了。 那么,这是 ROM。 它要重得多、 而且它的 SGOT 是一个更大的摩擦 大电压系数引起的。 它的 衰减速度非常快。 这是质量 M2 、它受到影响 到更大的程度。 很好。 这 两种情况下会发生什么情况 会在 该幻灯片上缓慢地摆动 Way: 他们在 幻灯片上进一步休息了大约法米 比他们开始时要好很多。 因此、我想您可以通过 执行 BOOING 来实现这一目的、就像这样、 它将 稍微振荡一点。 然后它最终进入 GTO 移动并休息。 就是这样。 如果 我们有如此倾向、 构建该图的波特图。 为此、我们启用 了传递函数 表示 好,就是这。 现在、这证明 存在 SAN 集成。 因此、极小 的 leigenvalue 为0。 然后、我得到 了共轭偶极 和 一个实极点和一个实0。 所有这些东西都可以 在波特图中进行初始化、 样子的拓扑。 因此、我们有一个积分器 、负90度、然后 有一 个共轭共轭极对、它 提供了这个和那个。 然后、这里有一个极点、 真正的极点和一个真正的0 在这里的某个位置。 这些是校验器的校验器。 我们将 更详细地进行检查 此常见问题解答 现在 剩下的是唯一一个细牙 是我最喜欢的部分 、即测验。 类似 矩阵有什么共同之处? 它们相似吗? 因此、它们 是通用的。 [INAUDIBLE]? 是的、它们确实如此。 是的、它们确实具有 名称值的数量 帧周期和帧数。 这不是 我要找的答案。 但这是一个很好的答案。 我 要寻找的答案是他们 用 二表示 Sam 的系统化 不同的坐标系。 但 你绝对是对这种情况的。 在过去,这主要依赖串行总线 模式表示法的两个优点。 我想此时-- 简单 您是对的、简化。 从输入 和输出到输出的路径 可视化效果要明显得多。 [听不清] 对,是的。 因此、由于 我们刚才所说的第一个属性、 证明其正确性。 可观察性、 以及可检测性 10K 欧姆的电阻器。 所有这些东西 都更容易实现可视化 在构建 可控制性矩阵时、 例如 ,寻找一个排名。 因此 、对这些内容进行视觉化要容易得多。 对于离散时间系统、内部稳定情况如何? [听不清] 您处于稳定状态。 说得对。 稳态输出。 因此、内部稳定性、请调用 另一个名称。 Michelle 知道、它具有 有限的输入、有限的状态。 那么、只要输入受 限、状态是否受限? 如果是、它具有边界 输入受限状态、 或内部稳定性。 这种离散时间会怎么样? 那么 CMTI 呢? 我们对系统的看法是什么 它是否具有内部稳定性? 对我来说、内部稳定性确实 是一个错误。 输入怎么样呢? 稳定。 特征值必须是什么? [听不清] 对。 它将小于1 、或者如果它具有 Lyapunov 稳定、 它必须是 Equa LTO 1或更少该1。 是的。 系统是什么时候- 我刚才告诉过您。 离散 时间系统何时稳定 ISL? 还记得这是什么意思吗? 从 Lyapunov 的角度来看、它是稳定的 当 eigenvalue 剃须一个幅度时 大于或等于 1 因为实际上严格地说 是 Lyapunov 稳定性 还包括渐近 稳定性。 我们如何确定 给定的状态空间 是否在工作。 我为您提供了两种方法。 第一种甲基甲基甲 基甲基甲基甲基甲基甲基胺 模式分解。 我们对铁蛋白模式分解有何看法? [听不清] 是的。 是的。 模型输出 Matri x 中没有0列。 模式输出矩阵的每个列、 它们是伽马1、 伽马2、伽马3。 每个伽马耦合的对流二极管都朝向输出。 因此、只要这些 gammas 都不是0、 你知道所有 的表情都是通过耦合的。 因此 系统是可以观察到的。 还有一个测试。 [听不清] 是的。 您构建了 可观察性矩阵 Q 它是 C 转置、 转置、C 转置、 这些分区。 它应该具有 N 的全排名 观察性矩阵。 因此 、有两种不同的方法来确定它。 太棒了。 如何观察 可控制的规范表单 相关 我要找一个词。 双性。 它们是彼此的双重结构。 我 通过转置将系统矩阵相关联。 可见的系统 mmatrix、OCF 矩阵 是 CSF 系统矩阵的转置。 然后、您有 可控制的 B 矩阵 是 C 矩阵的转置、 观测 用例、反之亦然。 是的。 可观察性是 我一直在寻找的字。 我将为您提供该值。 QFN/SON 是什么? 它是什么? 它与 状态矢量的大小有关。 它只是 一个具有最小尺寸的系统 向量的 这就是它的样子、 换句话说、就是很大的尺寸。 与 FRAM 有什么不同?” 和 ARM™ [听不清] 是的。 那么、可检测性-是的。 我知道您的意思。 解决了可检测性问题 不稳定模式。 这意味着您可以 通过观察来检测不稳定性 输出端发生的情况。 现在、我们将 花一点时间吃午餐。 但在我们这么做之前 、我要感谢您 在 过去三小时内引起您的注意。 因为这是一项艰巨的工作。 它似乎很抽象。 其中许多是数学运算。 它看起来不像我 在做任何真正的事情。 但今天下午 、请回来。 因为我们 将获取这些信息 要控制双质量系统等系统、 飞行控制器等令人兴奋的东西。 我们以 非常真实的方式使用该信息。 所有这些东西对于 今天下午的到来都很重要。 因此 、对于那些从 TI 外部加入的引信、 我们在回退时看到了一些袋子 吃午餐。 我们将 在1点处恢复、 请重写 第7章。
线性系统的属性 、那么我们的介绍
熟悉 我们的房地产空间配方、
以及我们如何从中提取认证 信息、
包括矢量 和矢量值、
然后是动态 响应
之间的连接时, 优先考虑 MOSFET
表示法和 transfe 函数表示法。
该段 会进一步变小、
并检查 状态空间公式的属性。
尤其是、
非常重要、还有几个
想象 不到的其他人。
最不可避免的属性
是稳定性。
您可能会看到非常清晰的图像
我所说的稳定性。
很明显 、对于稳定的系统、
对于连续时间系统 、甚至是传递函数
稳定意味着什么。
您在看到它时就知道它。
它要么 是一个细长的 gthat 仍然绑定、
或者它不 会重新绑定、这很好。
但对于 stat 空间描述
其中我们有一 个内部变量、
稳定性分为几个级别
认知很重要。
当您进一步讲德语时、
如果您继续了解双头螺栓 非线性系统、
你会发现稳定性确实 是一个非常可怕的概念。
有这样的系统 外观
就像它们是稳定的、 看起来就像它们一样
同时在重写。
因此,我需要从 国家的角度解释稳定
空间说明, 特别是从状态开始
CEO 观点
然后,还有交流损耗。
这些是对资产空间描述的唯一性。
这些称为可控 性和可观察性。
它们不适用于 etransfer 函数描述。
但它们确实适用于 空间描述。
它们非常重要。
因为当我们稍后使用 进行设计控制系统时
状态空间模式、即系统 无法控制、
我们的努力将是徒劳的。
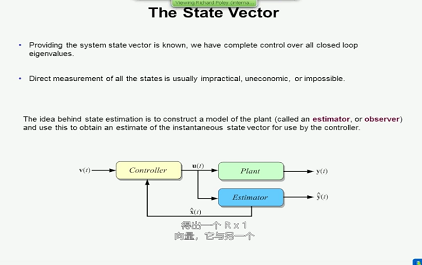
稍后 、当我们开始设计时
估算器或观测器 、这是相同的、
如果无法 观察到我们开始使用的系统、
同样,我们的努力 也是徒劳的。
我们无法从 无法观察到的系统估算 estat。
控制能力 和可观察性
是 我们稍后需要的重要属性。
现在、事实证明、稳定性 以及可控性
和可观察性、 所有这三项
如果 我们可以执行、就会有非常清晰的可视化效果
特定的近亲 DOF 变换
在系统上调用 da 模式分解。
我将向您解释 一下实际的模式分解
方法。
但是、如果您可以执行 eout、则会执行所有这些属性
您会非常清楚、 并且有好处
也是如此。
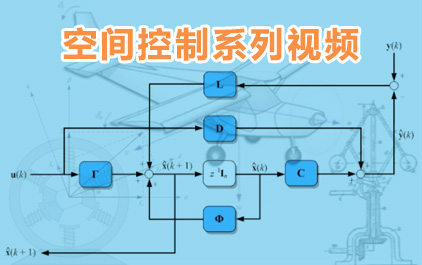
因此、我们将从 模态分解开始、
我将向您展示 所介绍的属性
以及 其他方面的术语。
然后 、我们将再次查看标准化的实现。
我向您展示了一 种、phas 可变规范形式。
事实证明、它 是另外两个被称为的位
可控制的规范形式 和可观察到的规范
因为此处是三角波形。
这就是为什么这个部分 恰好出现在那个部分之后
控制 能力和可观察性。
然后 是我要做的最后一件事
这 是一个 fairl yshort 部分、
最后要介绍的是冲头
下一个教程、我 将会或多或少地
每个教程都 将基于该教程。
它是一个双质量系统。
它由一 个有两个质量的机械系统组成
耦合在一起、
这样当你推动 水体时、其他质量就会移动。
但 两者之间存在某种能量交换
质量。
结果是振荡。
这是一个很好的、易于视觉化的系统。
它具有很多动态特性
让这些教程 变得有趣
这三种运动。
所以,我要启用系统。
驱动 ZVS 转换。
现在、我想先 解释一下这个概念
矩阵。
当矩阵使用 dfor 变换时、
您已经看到 、在 n 维度中、矩阵具有尺寸
n 乘以 n
矩阵为方形。
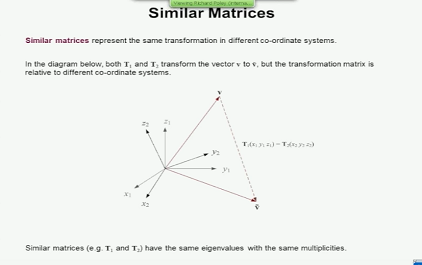
因此 、如果存在转换
在 三维空间中、从一个矢量到另一个矢量、
变换矩阵执行 三维变换。
例如、在这里 、我们有一个矢量 V、
它不由矩阵 T1运行
将矢量 t oa 变换为不同的矢量
V tilde。
因此、V tilde 是指向 不同方向的点 Gin
因为 它是由矩阵 T1进行操作的。
现在、T1、如 Wel las V 和 V tilde、
将以该坐标系的项 s表示
或者二者都是复数。
例如 x1、 y1和 z1、它们
可能是正交坐标
它代表矢量 和变换
权衡关系。
现在、让我们想象一下 、我们什么都不会改变、
但所有 这些信息都是坐标系
演示。
我们不使用 x1、y1、z1、而是使用 x2、y2、 Z2.
嗯,现在,相同的 tw omatrics-相同 的两个矢量
具有 slightl ydifferent 表示法。
因为它们的元件 将会不同。
因为它们 虽然指向相同的方向
从理论上讲、它们 在中重新呈现
不同的坐标系。
以及变压器 矩阵
从 V 移动到 V tilde、 这也会有所不同。
因为它的协调 帧发生了变化。
它在做的是相同 的事情、
但它是在 adifferent 坐标系中执行它的。
矩阵 T1和 T2 试用相似的矩阵。
它们可以实现 相同的变换、
但它们在 adifferent 坐标系中执行它。
它们与 所谓的旅游相关
相似性变换。
具体而言、T2 i 序列到 M、再到-1、
T1乘以 M、其中 M 是 相似性变换。
它将 Matri x 从一个坐标系变换
另一个坐标系。
且在 500 MHz 下,其 IP3 为 [听不清] dBm 时
不是吗?
您可以看到矩阵 M它必须进行测量。
它必须具有 与 T 相同的名称尺寸、
因为 T2的 esame 尺寸与 t1相同。
但是、当 你看到它时、M 乘以-1、
考虑相似性变换。
它将在 一秒内进入 com ein。
请注意,这是一个重要的属性,
那么、让我 花几分钟时间来讨论它、
难以仿真。
可以找到类似 的变换矩阵 M、它
采用 T1并使 T2对角线。
如果您可以 执行该操作、则会出现该情况
是 产生的许多好处
系统的电感。
该特定坐标系。
但 为了实现这一点、t1
必须具有一 组完整的特征。
否则、您可以 对 T2进行 tdiagonalize。
如果 T1没有一 组完整的特征向量、
您不能具有对角线 T2、
但您可以接近它。
出现的仿真形式、
称为 Jordan、用于 mrepresentation
稍后我会介绍。
但现在让我们想象一下,我们 已经不会有一整套特征的特征
这种 SoM 相似性变换可以实现
从而 使产生的 diagona lmatrix t2
该矩阵是对角线、bit 具有更进一步的属性
即您可以 对元素进行范围内的操作
对角线 Matri 的斜线、使其如此
以及系统的效率。
类似 的转变
这对你来说是一个 scolumns,它们本身就是这样
T1的特征向量。
这里有一些重要 的信息
一些特性。
如果 T1具有一 组完整的特征向量、
矢量 是定义的
CPU 独立
这些矢量 扫描用作列
以形成类似 的变换矩阵 M
因为 您知道、对于尺寸来说是可以的
你 有 n eigenvalue sin t1、t1是 n x n、
并且 您已经设置了完整值。
您有一个特征矢量。
每个特征都对 RHAS 中的元素感到羡慕。
因此、通过将这些列、 即 M、M 的列进行设置
尺寸也必须为 n b yn。
并通过使用 Matri x 实现相似性
变换、T2斜 线对角线、但不仅仅是
对角矩阵
T 1的特征值将是元素
对角线的对角线。
现在、在 我们了解该信息之前、
我 将向您介绍如何操作
您 可以使用状态方程进行状态变换。
现在、假设我 将一个状态方程式进行了打字
对于基于 关节状态选择的系统
影响。
我之前告诉过你 ,没有什么特别的
状态元素。
大家想用什么都可以。
那么、让我们假设 您做出一个选择、
它对 您来说并不是很有效、
您希望将它们更改为 不同的元素集。
没有理由不能这样做。
变化可能 会因所发生的事情而产生
称为状态变换。
那么、假设您使用的是 x 、并且您希望进行转换、
改用 v。 vis a different --
我是说它是一个状态矢量、但 我现在将其称为 v。
它与 x 通过 这个矩阵 M 相关、即
现在是 n 的任意矩阵
那么、我们要做的是将 这个直接置于状态
等式、x 点等于 x plu SV。因此、左侧不是
x 点不再出现、但它是 M 时间 SV 点。V 点是新状态
等于 AMV。
MV 只是插入之前 的 xwas,加上 v 乘以 u. v
不变。
现在、我们要做的是 、我的 SWE 将对两侧进行预乘法
与 M 的倒数相反、如果 您可以的话、现在这是一件好事
M 由特征向量组成。
因为 M 肯定 会反向。
因此、您可以 从 M 中找到反向
它是正方形的、因此尺寸 是我们所需要的。
爬虫 程序会以 M 的倒数进行预乘、
您得到 v 点等于 m t othe -1、乘以 M 次
五、看,类似 的状态转变
矢量。
加 n 到-1 乘以 v 乘以 u
我们执行 了相似性变换
在电压矢量上的优先权。
并猜测 负1 AM 矩阵的 MTO 值
变为负数的区域。
它就是带宽。
它 将在前导代码中具有该 eeenvalues
对角矩阵
我们要将其命名为 LPO。
让我们将 M t othe -1B、B1称为。
现在、这是状态向量 Rinto 转换状态。
我们现在需要集中讨论 输出方程。
可以执行相同的操作。
但它要简单得多。
因为我们不会 将 ETO M 反转。我们需要的一切
将 x 替换为 M 时间 SV。我们将其称为 C1。
因此、C Time M 将 变为 t obe c1加 v 乘以 UD
不受所有这些影响。
那么、现在我们有了 stat 公式和输出
该 新状态的 I nterms、v、
v 恰好是多少。
现在、独特的选择 -那么、这里有
无限选择。
您可以随意选择名称。
因此、我们不会将任何 特定状态绑定在一起。
您可以在 一个和另一个之间切换频率。
但对于这种声波 ,v 的元素
有一个特定的名称。
它们被称为 系统的表情。
典型系统运行 I nCharacteristic Set of Patterns、
梯形脉冲。
这些模式称为模式。
它是 状态矢量的电子元素的唯一选择
这些称为模式。
这之所以很 重要的原因是
您将看到 每个模式的时间
与所有其他模式完全解耦。
这种变换、 独特的变换
其中您使用了 eigenvector 列的 Mmatrix
转换为-使用 我的 neffect 矢量变换。
这称为调制 分解。
在以后您了解到 自己可能希望
第一个是 、事实上这些模式是不耦合的
彼此之间、可 提供非常清晰的可视化效果
放大数模转换器和输出之间的信号。
不仅是这样、而且通路 从状态中的输入端
到输出 的状态要清晰得多
如果 你刚刚采取随机状态、你会更好
矢量 MAPS
动态特性 更易于解决。
因为存在 标量、而不是矢量。
您可以对 随时间变化的运动进行非常简单的视图、
它使 系统的动态变得更加清晰。
因为通过公开这些 值、
您知道哪些是主要模式、
这一点不太重要。
请记住 复平面中的电子滤波模式、
复数中左侧的特征值
比 那些衰减得多
在右侧、它们接近 虚轴、
如果它是一 个持续计时系统、那么它们就会被执行
与我 FIT 的离散时间系统并联。
您还可以 获得更清晰的见解
介绍了 tw 属性
更早的可控 性和可观察性。
我 认为通路暴露在外的原因
实现平衡。
该过程在 一段连续的时间内类似
奈奎斯特路径。
只是曲折 的特征值是不同的。
那么,让我们来执行它。
我们将编写 模态相似性变换
我 现在将其称为 W、
因为它是一 个非常具体的转换矩阵。
M、但 我想将其称为 W
由 列 sof W 组成
独立 的特征向量的特征向量
矩阵 A。因此您不需要 对列进行调整、
每列都有 n 个元素。
这是一个 n x n 矩阵。
我将为 该矢量添加符号
因为经济转型也是如此具体
以及 称为模式的独特选择。
我将为 符号 q 进行 E过渡期、
元素 wil lbe Q1到 q sub n
有 系统的模式。
是的。
就是这样。
现在 、存在 r表示 法变化
我想让您知道。
这是 EMI 滤波器部分。
这里是 输出端。
因为这 是一个独特的选择
的列数
W、正如我说过的、我们最终得到 了一个令人激动的新系统
矩阵 DMS
这是一个交流电机。
Lambda 将沿其前对角线包含
A 的特征
那么、写入这些方程 、Iguest 这就是它们的外观。
扇 出的模式矩阵包含在其列中
A 的特征向量 和频谱矩阵、
因为它称为 Lambda 、所以我对角线矩阵在这里
特征值位于 主对角线上、
所有的 释放都是零。
模态矩 阵
是应用 于这两者的名称。
现在、模式输入矩阵是 W 到-1乘以 v
我们将把 W 插入 状态变换公式
那个方程。
我已经解释过的 λ。
现在、输入矩阵 、W 至-1
v。当您 进行此分解时、
将 该输入的各个行分开很有用
矩阵。
因此、我一直将这些行 称为 sbeta 1、beta 2
至 β n
这些是 WTO 的负1 v 行,即
为什么我这么写。
可以将其视为变量。
但实际上 、它们是行矢量、
现在、输入矩阵的第行中有 n 个。
输入 矩阵的 Beta 1和 beta n ar ethe 行、
W 至-1 V
因此、这会 影响您的状态方程
看起来像完整格式。
左侧的模型矢量的导数
等于频谱矩乘 以模态矢量、加
然后、这些是 新模式输入矩阵的行 s.
但我想它们是 一个矢量乘以输入矢量。
如果您愿意、它 将为我提供测试版
捕获所有 电子输入到特定模式的耦合。
然后、Lambda 我捕获 从 Qi 到 Qi 点的动态。
那么、您现在看到了我的意思、即完成 去耦。
如果您可以用 此表单编写 estat 公式。
那么、这是模 态输入矩阵。
这就是它在 到达单个模式时的外观
您得到的方程。
那么、现在请注意 、这个 Lambda 我出现在这里、这是
是完全标量。
关键点是 动态不耦合。
输入矩阵。
现在、模式响应、之前 的每个状态派生
可能涉及 所有其他状态。
因为 状态矩阵可能有一个 da 行
它 一直具有非零元素。
但现在你得到的是我 只需一个一阶
差分方程、 涉及相同的模式。
其他模式不 会产生任何效果。
这是模式的分辨率。
因此、它是用来 修复瞬态响应的特征值。
这将为您提供 模式演进的增长或衰减。
然后、参与 积分涉及 β I
这样我们就可以 得到响应的整形
是 确定该值的矢量
通过 与 B.的关系
输出矩阵 I sthe 乘积为 C 和 W
这对我的想法很有帮助
作为 单独的向量。
此外,可能会发生击穿,这可能
因为该 wil 向上乘以向量。
因此、伽马1至 GAMM an、单独的矢量、
每个矢量对 成个单独的-一种单模式
所有输出上。
那么、这就是我 应该看到的样子。
我是说它们是向量 、但考虑它们
现在至少是标量。
正如我所说的、每个伽马我 都会闪烁一个特定的模式
所有输出上。
以便输出矢量 等于所有这些乘积的总和。
因此伽马1乘以 Q1、plu sgamma 2乘以 Q2、依此类推。
现在、我认为这个图 将把它全部绑在一起。
因为这是我们 所做的所有图形。
我们已更改了显示方式
完全 独立的套件
状态、每个状态 都是完全的
去耦所有其他的。
现在为 729。
因为 Qi 取决于 y 点、反之亦然。
以及空间与所有输入之间的耦合
由相应行的低确定、
输入矩阵的输出。
以及所有输出之间的耦合
由模态输出矩阵的 I colum n 决定。
那么、您现在可以看到吗?
您已经获得了非常清晰的可视化效果
所有输入 如何影响一种模式、
以及 MOD 如何影响所有输出。
这 种表示非常明显
发生的情况。
现在一切都正常、 前提是您已经完成了
一整套 eigenvectors。
如果您没有 、那么您可以使用的单向方法是这样的
如果您使用 了树形特征值。
那么、在我向 您介绍如何操作之前
您使用这些 信息来描述
我 想要的属性 o fa 系统
简单地轻触一下 、如果您有问题、会出现什么问题
有一个去生成系统矩阵。
它只能通过 反复的特征值来实现。
即使这样、我 也可能不会发生。
你可能会幸运 、可以说、你已经成功了
才会出现退化。
但您仍然有 一组完整的特征矢量。
或者您可能运气不好 、丢失一个或多个
铜。
因此、系统会发生退化。
当您遇到 eigenvectors 时、您必须
如果您要执行 TA 模式分解、
您必须 替换 mby、替换缺失的
具有 被调用的矢量的矢量
广义特征向量。
这些 仍将是真正的特征矢量的正交。
但它们不会 满足矢量的要求
我 在前面展示的公式、它是什么
是负 λ i、乘以 WI。
我们寻求 了一种微不足道的解决方案。
因此、它们会对 特征去变体进行泛化。
您可以在网站上找到这些信息。
有一个很长的 yprocess 可以找到它们、
我不打算 在今天的研讨会中讨论这些内容。
但一旦找到 了它们、您就可以使用它们
实现平衡。
但频谱矩阵、对 角线 eigenvalues
不再 是真正的对角线。
它 将在斜升对角线中有一些元件、即1。
这意味着电 极二极管不会完美
去耦所有其他的。
将会有一个小的耦合 EBIT 开启。
Matxri 的形式 具有该对角线、
但某些受支持 的对角线等于1。
它们称为 Jordan 矩阵。
矩阵、即 生成的系统矩阵、
或频谱矩阵、其中 有 Jordan 块。
现在 、在时会出现可能的差分排列
您开始丢失矩阵。
但从根本上说 、特征检测器的编号是
实现的最大值
取决于您 的解决方案
获取公式 A minu si 乘以 λ i 再乘以 WI
α1α2 = 0。
这就是你发现了这些嫉妒者的方式,你还记得。
你这样做是为 lambda i 的选择
现在、我的 λ 一定 是可耻的、您可能会失去解决方案。
您可能没有完全 独立的解决方案。
您得到的数字取决于
在空空间维度 o fthis matrix 上、A 减 I 次
λ I.
空的 spac eDimension 会告诉您
您 将要获取多少个电子矢量
该特定的 Lambda I.
在本例中、 有一个整数
我叫 calin ghi、告诉你
可用 特征向量的数量
放大器驱动电路。
且 numrbe 介于1、
你将始终得到 1、而 Mi
特定 特征值的多重性。
如果您幸运、您可以使用 GE TA 全套、在这种情况下
你已经得到 了完全不一般的东西。
我们无需担心。
但是 、如果您没有这么做、
嗯、如果 你只有一个、你
需要这些通用 的去 igenvalues、
最后得到完整 的 Jordan 表格展示。
如果 您具有介于1和多重性之间的
你最终 会看到 Jordan Blocks 出现。
频谱矩阵 x 中有特定的块
它们具有1的超级对角线。
但它们并非全部为1。
它们中有些被压入。
让我来向您展示 一个有关这方面的快速示例。
这可能是一 个 Jorda 挡块
与特定的值相关联
具有一定的多样性。
同谋 是数字
对角线上的元件数。
您可以看到 、所有元素都是0、
但这几个除外。
这称为 Jorda nblock 或 Jordan 矩阵。
因为这是唯一的矩阵。
例如 、这里是一个五阶系统、
它具有三个特征值。
这有两个主要目的。
我有两个在-2处 、两个在+ 3处。
这 是一个不稳定的系统、1位于-1。
那么、在这个 scase 中、会出现什么
是 针对负2处的 tw oeigenvalues、
有一个约旦集团 的 kof A。你看到了吗?
它位于对角线上、 因此特征值
XY 尺寸更小。
但我们 需要的广义的 eigenvecto 在那里放置了1。
然后 、对于3、还有相同的细 gg
一个 Jordan Block 出现 在 ghere、对角线上有3秒、
对角线中为1。
然后是单 个特征值
给了我们一个 与它相关联的嫉妒。
因此 、您会在右下角得到一个很好的-1 i
类似情况。
现在、我将执行 一个快速教程、
只是为了向您展示 如何使用模式分解。
一次、它不再是 这些降压转换器的基础。
当 我清除其他一切时、请与我保持联系。
在本例中、我们在教程6.1中
分解-- 我不知道我做了什么。
为此我 道歉、我按下了一些东西
我不应该把 它分解
组成模式。
那么、很显然、这是 一个三阶系统。
我不知道它 将是怎样表现的。
但它显然有两个输入。
因为输入 Matri x 中有两列。
因此、我们有三个状态、 我们有两个输入、
我们有单 输出、因为
输出矩阵 C 的形式。它有一行。
因此必须有一个输出。
它具有 thre ecolumns、因为我们
知道有三种状态。
输入矩阵为0 - 转换矩阵
很抱歉、是0。
它包含两个元素。
因为有两个输入。
它有一行、 因为有一个输出。
那么、让我们分解 成它的组成模式、
看看会发生什么情况。
那么、首先、我们 要做的就是 hthen
使用 与我相同的方法构建系统
之前在 MATLAB 中展示的。
在我们进行 模分解之前、
我将绘制其响应。
我们将看到其 响应变化
模式分解后。
首先、我 将要构建
阶跃响应 、并绘制三种模式。
现在问题是 、这里有两个输入。
那么、阶跃响应 、问题是-原因
它 有两个 Pste 输入。
因为当 您执行一个步骤时、MATLAB 会对 LDO 产生什么影响
具有两个输入的系统上的响应是
有两组结果。
一个是 施加到第一个输入的 ste、
而第二个保持为0。
另一组结果 、当第一组结果保持为0时、
第二个应用 了阶跃输入。
因此 、这里将会有状态图的 tw oset。
它将反映 状态的维度
由此产生的矢量、 状态矢量结果。
我们可以开始了。
仿真结果如下。
上图是 三种内部状态的演变
当我们有阶跃应用 程序 dto U1、U2保持为0时。
然后 、在这里的底部图中、反向是
这些是 随时间推移的状态解决方案
因为 U1保持恒定、 而 nu2施加了阶跃。
现在、我们要做的是 perfor ma 模式分解。
我们就是通过这种方法来连接它的。
此 CLC 只清除 工作区中的任何内容。
这使事情 对我们来说有点整洁。
然后、我 将再次执行 EIG 指令。
请记住、这是 从中提取的特征值。
但当您使用 这两者的结构时
电 容、电容和电容参数
将返回模态矩阵 W、
频谱矩阵 λ。
嗯 、键盘对 lambda 没有注意。
那么、我将使用大写的 L
这是两个矩阵 、n x n、3 x 3
在这种情况下、将返回这些值。
您为其提供系统 mmatrix a、而不是仅提供平衡
意味着不要平衡 特征检测器、
我的意思是,我只是把 电子贸易机会这样做。
没有关系。
现在 、你已经把 W 变为原来的值。你可以
在类似 的变换中使用它
提取模式输入 和模式输出矩阵。
请记住、模式输入 Matri xwas W 到-1乘以 B
因此、我们将反转 W、 并将其乘以 B
我是雅斯特- 嗯、
我将断开它。
因为我很感兴趣、所以我 将行视为向量。
稍后您会看到。
然后、模态 outpu tmatrix 为 C 乘以 W
然后 、OIS 将代表它们
作为电流 LSB。
我们来操作一下。
您将看到 A、B、C 和 D 消失、
我们最终获得 L 和 MIM 0和 D
我不知道为什么 w EDID 不会结束-好的。
好的。
因此、它所做的就是再次为 我提供 A、B、C 和 D。
但这点我 是作为频谱矩阵的点。
这是 以指数值的 gof 表示的 λ
实现平衡。
这就是 EN/UVLO 引脚。
很好。
我想知道为什么它会被转置。
这实际上是正确的形式。
我不得不思考 为什么它被转置了。
但这是 输入矩阵的巨大形式。
因为它有两列。
有两种方法。
然后,还有交流损耗。
因为 其中有三种状态。
然后是 outpu tmatrix、模态输出矩阵、
透射 性 nmatrix 仍然为0。
我们现在将 执行相同的操作
我们在 Carrie dout 模态分解之前做过。
我们将进行预设 、并绘制状态。
现在,这是问题所在。
对于这种特定的状态选择、
因为我们有一 个完整的对角化光谱矩阵、
我们现在必须具有完全去耦内部状态。
每个状态 都取决于其自身的状态。
因此、我们得到了等于 λ i 乘以 Qi 的 Qi。
它们耦合在一起。
它是第一 个 orde rdifferential 等式。
这里没有其他东西。
您从过去就知道 、一阶解决方案
差分均衡 呈指数级。
因此、当我们计算 并解决这些问题时
对于阶跃输入、我们应该找到 1减去指数衰减
代码。
我们得到的确实是这样。
那么、这些是状态 、以及它们现在是如何演变的
变化情况。
因为它们 彼此去耦。
您可能会看一下 并思考、嗯、好的。
他告诉我们。
那么、什么。
可能系统也发生了变化。
但我 的观点是、它只是这样
系统实际动态的状态变换
不变。
换言之、 整个系统
无论 我是否表示、行为都完全令人感到羞耻
使用 SoM 耳本选择的状态、
或这个特定的选择。
我将向您展示这一点。
现在,我要 做的是,我要
绘制原始系统。
Y1的图、这是 原始系统的输出。
第二个传感器已经成功连接。
好的、这 没什么特别有趣的。
这就是系统的行为方式。
现在、我在 这里的 GTO 中所做的是、
这是一回事。
我将绘制 该图 Y2的顶部、Y2
是发射 分解的输出。
我 希望、所有这些变化
是该图的颜色。
它应该从蓝色变为绿色、 因为它是同一个系统。
它只是国际 动力学
以不同的状态选择表示。
这就是调制 分解为我们所做的事情。
[INAUDIBLE]?
使用 GA 模式分解的主要原因
从 mthe 输入到输出的路径
更清晰。
该属性意味着 可控性的属性
和可观察性、 可预测性等
更容易实现可视化。
看到 GPIO。
没错,这是问题的关键。
因为它会引导我 了解接下来将要做的事情。
[INAUDIBLE]?
是的、这是可能的。
[INAUDIBLE]?
嗯、它会使 引脚感到它
可能会将注意力集中 在非主导模式。
因此、它可能在这方面有所帮助。
或者您是否希望 简化系统
通过减少它的 orde rof、它可能会对您有所帮助
做出该选择。
因此、我 需要在控制设计方面提供帮助的原因有很多。
[INAUDIBLE]?
是的,确实如此。
[INAUDIBLE]?
嗯、有点像。
对,很接近了。
但我想摆脱 超前和滞后的想法
补偿器、也 是根轨迹的除法器。
因为在 系统中-我昨天介绍过
其中我们使用 doutput 反馈、我们
必须 关闭闭环
特定线路上的极点称为 loci 的复平面。
我们 可以更改的唯一精简 gg
是增益、沿 这些轨迹移动轨迹。
状态反馈控制的一大优势
您可以在 复平面中任意选择您喜欢的任意值
放置极点。
您具有极大的灵活性
接近 的环形极点所在的位置。
您 正在使用的栅极、FAC
而 不仅仅是输出中的状态矢量
好处。
因此、我认为这有助于 推进这一决策过程
极点的选择。
现在、我 将稍后更多地使用该小数位。
但我想 在一段时间内继续保持 kabout 稳定性。
那么,有两种 类型的函数。
在 我们继续之前、我想告诉您、
并了解如何使用它们。
第一个问题是,我们 可能会立即这样做
视为稳定的系统。
这一制度占有 财产
称为渐近 cti 稳定性
这意味着它的状态 i nthe initial condition
随着 时间的无限变化、
将收敛于该 电子平衡点。
因此、这相当于一 个稳定节点或一个稳定焦点
在我 之前向您展示的相位纵向中。
因为这种状态 会跟随某种路径。
这是一个稳定的焦点、 最终会随着时间的推移而出现
它稳定地稳定 在平衡点。
它称为渐近稳定性。
对于什么、有一个字的 ydefinition
这意味着、就 可以在多大程度上取代初始条件而言、
它与 平衡点收敛的事实。
因此、具有 连续时间值的系统
小于0、或者 如果是 rdiscrete time eigenvalue
小于 1的模数、具有属性
渐近稳定性。
现在、在 本幻灯片中、我能不能
做一些看起来 很明显的事情
您很清楚、 这一点非常明显。
因为它稍后很重要。
在稳定状态下 、对于渐近稳定系统、
如果是连续时间、您 知道稳态是
由 T 等于0的 x 点定义。
这意味着 estat 不再改变。
它达到 了它的固件点。
那么这是稳态。
但请注意、如果它是 离散时间系统、
存在陷阱。
因为我 在稳定状态下的意思
是 nex tstate 没有不同
输入和现态。
状态 XK 加 1与 XK 相同。
因此、当你保持 稳定状态时
对于分立式系统 、重要的是
右侧 不再是0。
这将在 我们看设计时再次出现
控制 系统中的稳态的高电压基准。
但我想提醒 您注意这一点
一个重要的差异。
实际上 、这是唯一的一个
稳定部队的差异
时间和 离散时间系统之间的差异。
因此 、稳态定义存在差异。
但无论如何、我认为您 可能[听不清]
想象一下,“那是一 种很棒的稳定。
现在 存在某种稳定性、
它位于 phas 纵向图中
其中平衡 点被称为中心。
一般而言、我 称为 Lyapunov 稳定性。
Lyapuno v컈 뚨 所说的是
如果您将初始 状态从其平衡状态中移位
然后让它运行、 前提是您没有
让它从 该状态转得太远、
它将对 状态进行收敛、
也可能不会达到无穷大。
它可能会保持 在平衡的每一个特征中
不 会在比赛中到达它。
这是 一个系统示例
它具有复杂的共轭 值、如果它是连续的
时间、或单 个转盘上的电子值、如果它是离散时间。
因为这些振荡 是持续的。
它位于边界上、不稳定。
它称为预翘曲。
有时您会看到具有 Lyapunov 稳定性的系统、
被称为稳定的是 Lin 的 Lyapunov 感。
这不是我们担心 的事情。
但术语会不时出现 、尤其是
非 线性系统的应用。
但执行 此操作的系统、在本例中
它是二阶 的、它的相位纵向会是
属于 中心的类别、
它具有利亚普诺夫稳定性。
现在 、绘制了两个车床图
就输出而言, DPWM 模块 2 和
此电路的频率响应。
我将讨论的是、没有 WIS 如何涉及输入。
因为 输入的有效性允许
我们将在 内部和外部进行区分
稳定性
首先、 内部稳定性是
耦合的属性介于 输入和状态之间。
它有时称为边界 性状态稳定性、
或 BIBS 稳定性。
有时、它是回调 式内部稳定性。
因为我们在谈论内部 变量集
称为状态。
提供 RA 有界输入、
状态保持 受限
获得 BIBS 或内部稳定性。
如果您解决 稳定性的均衡问题
主动能量传输。
显然、您正在寻找 外部信号。
以及 外部稳定性
当有界输入仅 产生有界输出时定义。
您具有 BIBO 稳定性。
现在、因为输出均衡 仅是代数方程
涉及到状态、则会提供 有界输入
有界状态稳定性、您会 自动获得有界输入
宽输出稳定性
因为在 该状态下、动态特性仅在那里
但不会相反。
这并不一定是一 个关键问题、因为系统是这样的
外部稳定、 内部稳定。
要确定该值、 您需要确定
状态如何从 内部耦合到输出、
主动能量传输。
您可能具有内部状态、这些状态
会像疯狂的那样振荡、但 不会耦合振荡
到输出 电流、因为存在
是输出矩阵中的0个元素。
因此、内部 稳定性是肯定的
可保证外部稳定性 、但不会相反。
好的,
现在、让我们来了解 一下可控性
10K 欧姆的电阻器。
稳定性概念也 会进入这种情况。
我有她 的 eis 四阶
已 执行模式解调后的系统。
它与 我之前展示的图表类似。
因为每个 表情都是完全的
与所有其他组件不耦合。
输入和 每种模式之间的耦合
由 W 减1 B 矩阵的 sw 行确定、
以及从 EAC 模式到所有输出的耦合
C Wmatrix 的列、这些伽马元素。
现在、 这是 W 的异或响应行
负1 B、因此 Bi 转换器 是非零值和伽马 I
非零、很显然 、tmode 是通过耦合的。
因此、您可以说是 因为输入
耦合到该模式、 我可以影响该模式
来减少输入电压。
因此、我 所说的模式是可控的。
因为 CW 矩阵的相应 gcolumn
非零、当该 模式移动时、它是
某种程度上会影响 至少一个输出。
因此、这 种模式的情绪
观察到的相关事物。
模式1被认为是 可控制和可观察的。
您可以看到我 在这个图上进行了详细的了解。
因为您知道该 异或响应矢量、
Beta 1和 γ 1为非零。
现在想象 一下伽马2为零的位置。
这意味着该模式不 会耦合到输出。
我们无法 通过观察输出来确定 gSimply
Q2是否稳定 EOR 为不稳定模式。
因此 无法观察到 tmode。
但由于 β 2是非零、 因此它与输入耦合。
因此我们可以对它施加影响。
这 是一种可控但无法观察的模式。
当 reverse 为 true 时、您可以
看看 模式3会发生什么情况、β 3是零、
但伽马3不为零。
因此、这种模式是不可控制的、 但至少可以观察到。
最后、有一种模式 、它与任何东西都是解耦的。
它是一 种无法控制的模式和一种无法观察的模式。
因此、这些属性 非常明确、
模式分解后、它将立即开始运行。
首先、 正如我说过的、它们的重要性是、
您无法确定 任何相关内容
内部可控性从 传输中循环伺服
功能描述
这些只是 状态空间描述中的属性。
幸运的是、物理 系统
控制 器和可观察的、
这意味着、当您 从头开始构建 astate 空间模型时、
某种系统、 即实际系统本身
那么这里的电压将大于 VOH。
但您的模型通常 包含一些简化
或一些假设、意味 着模型可能不会
具有这些属性。
因此您无法 控制
系统或观测器的型号
您的系统模型。
如果您选择的 stat edoes 具有这些属性、
然后执行 astate 变换
不会更改属性。
因此 、您使用的 wha tstate 选择无关紧要、
证明其正确性。
和可观察性 是系统独有的、
而不是选择状态。
你往往有各种原因使稳定部队有问题。
最常见的原因是您 忘记了有极点
在 您的转账职能部门、您可以在此处取消或取消预订
或 等效的传递函数
说明中有 偏斜极点和零点。
但由于 其他原因、您可能会运行 int oit、
例如、对状态进行明智的选择、
或可能是国家数量。
这些东西也可能会降低 可控性
简称 WCT。
首先是包络。
总结 一下左侧的两张幻灯片 sago
IAR。
因为只是很喜欢 动态、
从 输入到模式的连接路径、
β 1和 β 2列矩阵矢量
为 SPI。
Q1和 Q2 与输入进行爬电耦合。
那么,这是一个 RAM 地址。
而系统在黄昏中是无法控制的
功能模式。
但它是具体的模式 2、这是不可控制的。
因为模式2未 连接到输入端。
Beta 2是一个0矢量。
这是 IC。
因为这个 特定的特征值
位于右半平面。
这意味着 系统不稳定、
无论如何、GWE 都无法做到这一点。
因为我们无法 控制不稳定模式的通量。
这种薄 的 gg 可能不是很明显
如果您只需要随机 选择状态变量、
以及完整的可变状态 器描述。
但 它可以避免雪的存在
系统中存在不稳定和不可控的仿真二极管。
这将在稍后引发问题。
因此,如果您 在这里有电阻,
分类是 可控和不可控的
非常清楚。
您只需查看 rnonzero beta i 矢量。
这 是一种查看事物的方法。
还有 一个代数测试
适用于一般情况。
代尔拜 ctest 就是这样的。
您首先必须构建 可控制性矩阵
从现在开始、我将调用 P可控性矩阵
这样。
现在、这是 calle da 分区矩阵。
我想这是 昨天的 Matri x代 数笔记中的内容。
一个分区 Matri xcontains 元素
它们本身就是矩阵。
eis 上的这个特定结构如下所示。
它是 B、A 乘以 B、A 平方 B、一直到 A 到 n
减1乘以 B。让我们细小 它的尺寸。
B、您知道、i n x r matrix。
它有 n 行和 r 列。
a 是方形矩阵。
因此它不会 改变行数
有很多类型。
AB 将 会进行仿真、因此是 n x r 矩阵。
A 平方 B、类似地、n 除以 r
因此每个 分区都是 n 乘以 r
因此 、整个东西中都有 n 列。
您有 n 行、您 有 n 次 r 列
一个示例。
然后、你所做的 是、你看一下它的排名。
现在、请记住 矩阵的侧面
是 最大非零决定因素的尺寸
任何位置。
那么 、对于这个矩阵、你可以得到的最重要的排名是什么?
你不能大于 n
因为它中有 n 行。
它有 n 乘以 r 列。
那么、您有一个输入。
它将 是 bEAN n x n matrix。
这就是 EMC 问题。
如果您有10个输入、它 将是10n 的10倍。
但它不能得到大于 n 的 bigge、因为你
需要一个方形 Matri xto 具有一个决定因素。
因此、你 可以拥有的最大的 RAN 是 n
现在、如果这个特定 矩阵具有秩 n、
系统是可控的。
您是怎么做的。
对于离散时间系统 也可以这样做,
唯一的区别是 电位变化、A 的 C、
B 的伽马。 否则、您将构建
控制 器矩阵、并对其进行评估
完全相同的方式。
您 可以说有 SoM 的表达方式。
如果您只有一个级别 o fv、其中 v 小于 n
然后您知道您 只能使用 v 可控模式。
您有 n minu SV 不可控模式。
因为其中 n 减 v Beta 检测器为零。
还有一些人在可 控制性指数中进行了定义
因为 它是必须具有的最小数量的分区
添加、直到您获得全排名。
嗯、无论如何、这是第三 个可控制性指数。
现在、可观察性非常 相似、令人惊讶的是、
令人震惊的相似之处。
我有一个问题。
请说。
[INAUDIBLE]?
是的。
[INAUDIBLE]?
当然。
[INAUDIBLE]?
好的。
[INAUDIBLE]?
你会说 滴滴不会改变。
它 将永远到达一零。
你们得到的是这个吗?
是的。
就是这个[听不清]。
它将如何激发?
是的。
答案 是、我在数学上讲这个东西
将永远保持为零。
实际上,我们没有这样做过。
存在影响 系统的噪声和扰动
实际上、您只是 不知道。
它不会保持为零。
但你已经确定了你 不能影响它的 FAC
低电压。
因此、无论发生什么 情况、您都无法更改。
什么都不会改变。
因为会 有激发它的 SoM e扰动。
然后实习 YIT 将会增长。
但从数学角度讲、您是对的。
没有什么可以激发它的。
因此、理论上、它 永远不会保持为零。
但这不是必需的。
是的。
这是 ROM。
音频正常吗?
是的。
好的。
因此、继续 观察、
没什么特别的。
我们解决 了可观察性的均衡问题
放大数模转换器和输出之间的信号。
它是 CW 矩阵的列 s
它为我们提供该信息。
如果它们都是非零、 那么-即使是模式
通过输出耦合。
因为 γ 1、即 refxample、决定了
Q1与 所有输出耦合的方式。
在左侧、有 一个可观察的系统。
它仍然是一个不稳定的系统。
因为如果 N 大于 0,
它是一种 弱实时系统。
大家可以看到这一点。
因此、该电子模块 将会振荡。
但至少我们可以检测 输出端的振荡。
这是 可观察性的定义。
右侧是 I hav EAN 不稳定系统。
我认为它具有相同的模式 、因此具有相同的特征值。
但这是不可观察的、 因为伽马2是0。
CW 矩阵的第二列为0、
因此、secon dmode 未连接
任何输出。
我们 没有什么可以检测到什么
第二种模式将会执行。
这 也有一个代尔拜克特尔。
它涉及形成 顶点矩阵
时间反转函数。从现在起、P
Q 将为 这两个矩阵保留 dd。
因为我们现在非常需要 GTO。
现在形成 了分区
从 C 转置、转置、 转置、转置
转置等。
您在 该矩阵中查找运行 kof n。
如果您有它、 则可以观察到 nthe 系统。
如果您没有 该系统、则无法观察到系统。
离散时间有一个并行
替换为 C 的系统
现在有两 个相关的附加属性。
其中第一个是 我的扇贝稳定性。
IO_SUP 与 RX_SUP 相同。
但问题是仅针对 不稳定模式。
我来举一个例子。
这是一个系统、它是 一个无法控制的系统。
因为我们知道 FIRS tmode 与输入不耦合。
因为 Beta 1为0。
因此、这个 modeCAN 执行它所需要的任何操作。
w eCAN 无法影响这个模式。
但它是一种稳定模式、 至少它是稳定的。
但是、第二种模式是不稳定的。
但它具有一 个非 Zer obeta 2矢量。
因此、它通过 输入耦合、
因此、w eCAN 会影响它。
我们可以稳定 输入的 b y 操作。
因此、我 可以控制该系统、
需要的电压电平。
但至少它是可以稳定的。
但可以设计它。
还有另一 个与此相同的 mter。
但它会应用于输出。
它称为预翘曲。
它是可观察的、但只能寻址 到不稳定的模式。
实际上、它是 Sam esystem、
但在这里、您已经获取 tgamma 1非零值、
第一种模式是耦 合到输出。
第二个问题是可靠性。
现在、这里的第一 种模式是不稳定的。
因此、它 是一个可检测的系统、
降压-升压解决方案的大门。
第二项要求源于
虽然它不可观察、 因为它是稳定的
则可以说器件具有 ELDRS。
这意味着、如果 涉及到一个 yinternal 振荡、
系统内部任何不稳定的东西、
至少您可以检测到它。
因此、我通过 两种方式定义了可控性和可观察性。
我已经定义了稳定性 和可检测性
是可控 性和可观察性
但仅解决 不稳定模式的问题。
下面我们快速测验一下。
因为这 真的很有趣。
我们将对 结构特性进行调查
四阶系统的性能。
我 没有任何 IDE。
因为我不记得 本教程是如何实现的。
那么,让我们看看两种情形。
首先 、我们创建系统。
这里没有 什么令人惊讶的东西、
仅使用 SS 和 A、B、C、 D首先、我们要介绍
进行稳定性分析。
现在 、MATLAB 中有一个手录。
您不必担心 像 eigenvectors 这样的事情
和特征值、以及在 左半部分计划中的工作情况、
或右半平面。
您只需键入即可保持稳定。
是稳定的、它真的需要所有的东西 、不是吗?
因此、 您所做的是、您键入的是稳定的、
或者它是稳定还是不稳定。
是的。显然这 是一个不稳定的系统。
我们还不知道它。
但它是一种电路外的 EOS。
现在、我们要在 GTO 中做的下一件事是检查可控性。
我首先要做 的是我正在看
显示了片上 SRAM 的大小。
这将告诉你维特 尼-现在如果你在这里键入1、
它将告诉您 行数。
如果您键入2、则 会显示列数。
因为 它们的尺寸为1、2。
但我知道 AIS 是一个方形矩阵。
因此、这并不重要。
这将告诉我 系统的尺寸是多少。
当然、在 本例中、它是4。
然后、在这里、我 介绍了重要的一行、
因为这是 可控制性矩阵的构造。
CTRB 构造 控制性矩阵
您 所需的两个抹香
为其提供 系统矩阵 A、
和输入矩阵 C
因此,我们 现在对 P 退了
我只需要了解 P 的级别
与 A 的尺寸相同、它
是系统的等级 和系统的尺寸。
如果是、 则系统是可控的。
如果不 是、则是无法控制的。
很高兴这 是一个可控制系统。
因此 、在那里的某个地方有一个不稳定的仿真二极管。
但至少它是可控的。
因此、您可以说 该系统是可稳定的、
尽管它不稳定。
现在、我们将为 可观察性做类似的事情。
我将使用构建 可观察性矩阵 Q
为其提供 A 和 C 矩阵、
然后再次检查排名。
希望运行 的 kwill 等于4。
不幸的是、它不是。
等级小于4。
因此 、系统无法观察到。
并尝试 去探索神秘之地
在这个系统的后面、我们 将进行模式分解
你会发现这是为什么。
那么、我们将 共同定义 A 的 EIG
为我们提供一 个模态 d光谱 矩阵、
然后计算调制 线性输出和输出矩阵。
这是下一个脚本中的目标。
我们可以开始了。
现在、在我们 进一步讨论这个问题之前、
一些属性 现在变得清晰。
因为我们所做的都不 是模态分解。
我们显然拥有 完整的一组特征值、
和完整的特征 矢量。
由于所有 这些值都不同、
因此,我们知道我们 不会成为一整套特征的特征。
但是、如果您看 一下它们、左半平面、
左半平面 、你得到的是加1。
这就是 系统不稳定的原因。
这里有一种积极的价值。
3号为正。
嗯、我们知道它是 一个可控系统、
所以 我们不应该感到惊讶
einput 矩阵的所有行都不为零。
但我们也知道我 无法观察到、
这意味着 模式的 SoM eof 不是
噪声有多少。
输出 矩阵的头两列
为0。
因此伽马1和 伽马2都是0。
但伽马3和 伽马4不是0。
我们已准备好 [?
我们有 ISO-21848。
我们有 ISO-21848。
现在、 我告诉过您的其他一些属性
稳定性 和可检测性。
那么、让我们 先处理稳定性问题。
这 是不可扩展的系统吗?
是的。
米歇尔说是的。
每个人都能实现 经济转型的稳定?
它是稳定的、 因为所有模式都是如此
RTI = 参考了输入
因此 、无论模式的音调如何都是不稳定的。
它通过耦合。
因此它 可以稳定下来。
这是可检测系统吗?
为什么没有呢?
好。
嗯,请思考一下。
可检测性是可观察性、 但仅解决此问题
ECG 波形总是延迟。
因此、我们不是处于 稳定模式的中间位置
不稳定的情况。
嗯、它是第三个 不稳定的模块。
因此、我们将提高 可检测性、
可观察性。
我们需要 CW 矩阵非零的第三个色谱。
就是这里。
通过观察 gthe 输出、我们得到了
至少得到 了这个东西的电子信息
变为负数的区域。
这 是一个稳定的电子和一个可检测的系统。
但这并不理想。
这是无法观察到的 、整体来看。
因此 、该系统具有这些属性。
好。
我希望我们几乎就在那里。
我们有两种形式。
我不打算对这个进行人工操作。
因为我已经完成了。
这几乎是午餐时间。
这是 phas 可规避的规范形式。
这两者之间的任何不同之处
我 在上一张幻灯片中展示了相位
变量规范对于 mon、它是标题。
它称为控制 器 ecanonical 表单。
您可以通过 我向您展示的过程来实现这一点
开始,
您会得到矩阵的非常识别的电子结构。
您可以从 系统矩阵中获取该值
其中所有 的不祥因子系数
显示在底部行中。
除 超对角线外、矩阵的其余部分为0、
即1。
这是因为状态的选择、 即状态选择
是相位。
B 矩阵、输入矩阵 、为0、除了最后一个矩阵。
C 矩阵、 输出矩阵、
包含 分子的系数。
当您看到它时 、您就知道您是
处理控制 器 ecanonical 表单。
它称为自动生成该表单
可控
今天 下午、我们将使用这种形式
设计状态空间系统。
现在 、有一个类似的形式、称为
可观察的规范形式。
我将 很快地向您介绍、
告诉你 滴滴的关系非常密切
与可控 性表单非常接近。
该矩阵是 可观察到的规范形式、
现在我将调用 OCF。
好。
您有 CCF 和 OCF、 您可以看到这些缩写。
OCF 系统矩阵 与 CCF 系统矩阵相关
锁存器。
这就是所有的不同之处。
现在来看看关断,
对于观测 表例形式、
输出为 经济过渡期
控制 器规范形式的矩阵、
这两者也与 转置相关。
在某种意义上、可 控制的输出矩阵
是 可观察输入矩阵的转置、
反之亦然。
接下来,请看这里的
观测 表例形式的矩阵、
它与输入矩阵相同
可控制的 canonica lform、只是转置。
因此、如果您了解 一下音调描述、
您已经自动 获得了另一个、
如果您现在有 转置、OCF 和 CCF。
现在、 当我们来到这里时、这些东西令人非常愉快
进行状态空间设计。
CCF 更改了状态 反馈的设计
非常简单。
和 OCF 表格让 观察员设计人员
简单的提示。
现在它们是 calle dcomp配套 表单。
它们通过 这些转置相互关联、
我在 上一张幻灯片中向您介绍的内容。
但是、这种关系我 非常强大、
您最初可能想象的更强大的功能。
这种关系的名称 称为 duality、
这意味着这两个系统 被这些矩阵所描述
相反的信号线。
因此、您可以选择 其中一个的可控性
检测 对方的可观察性、反之亦然。
因为如果您在寻找 P 和 Q 矩阵、
它们的关联 方式与我的关联方式不完全相同。
请记住、P 矩阵是 B 分区 B、A 乘以 B、
乘以 B
可观察性矩阵 I twas C 转置在 B 位置、
和 A 的转置 I nplace。否则
完全相同。
因此、当您检查 其中一个的可控性时、
您实际上正在检查 另一个是否具有可循环性。
这种类似的并行功能有助于我们以后的工作
详述这一点。
因为使用 的技术是这样的
电压反馈控制器的设计
与 您用于观测器设计的完全相同。
这是一件充满力量的事情。
因为您只 能获得一组流程、
您可以执行这两个作业。
在这一部分的最后,
我 将向您展示一个非常简短的教程
可能会出现什么问题。
有一个术语"最低 限度实现"
这意味着您找到 了具有最小空间矢量的空间矢量
可能的尺寸。
以及您的模型可以使用的 GIS 的功能
在那里有状态、什么 都不做。
保存的操作太多。
您可能有 第三阶系统。
但你不小心 给了它四个状态。
当你这样做的时候 ,事情可能会出错。
通常 会出现问题的是您
失去 了我刚才讨论过的一个属性。
例如、您会丢失 可控制性属性、
这意味着 UCA 无法控制系统。
因此、您必须开始 确保已经完成了
具有可控性。
如果没有、请看一下。
您是否在处理 实现问题?
为了说明这一点、 我将执行它
以组织形式提供、教程6.3。
这意味着、对 可控性和进行调查
三 阶的可观察性属性似乎无害
一个输入。
因为 B 矩阵是 acolumn 矩阵、并且有一个输出、
因为 C Matri 坐标轴是行矩阵。
那么、让我们在 MATLAB 中查看这一点、看看会发生什么情况。
因此 、从一开始就没有什么令人惊讶的、
我们将开始 建立这一制度。
命令窗口中没有任何显示。
但这些是 工作区中的 Matrice swover。
我们已经构建了系统。
现在、我们将确定 首先可控性、
使用过去 用过的技术,
构建 可控制性矩阵、
并确定其等级是否为
等于 系统矩阵的大小。
如果是、 则系统是可控的。
如果它不 是-嗯、它是不可控制的。
但令人高兴的是、这是一个。
因为系统 mmatrix 是3 x 3。
这是 P 矩阵。
我们正在寻找它 中的大非零决定因素。
实际上、它会发生 这种情况
具有非零决定因素。
因此 、该矩阵的排名为3、3等于3。
因此、这 是一个可控系统。
现在、让我们继续、为 可观察性做些令人遗憾的事情。
我们已经知道 n 是3。
我们不必重新计算它。
可观察性、这 是可观察性矩阵。
不幸的是、最大 非零决定因素是2
降低了 2 毫瓦。
在这里、它具有2级。
2小于3、这 是一个无法观察到的系统。
现在、为了找出 原因、我接下来要做的是什么
查看 传递函数的 stat
部分。
因此、我将 使用脚本转换 S STO TS
要转换为 transfe 函数描述、
然后 TS 从 它构造 G、即 etransfer 函数。
我们来看看这个。
简单地说、好的、 到目前为止没有什么明显的。
它是一个三阶系统 、其中包含两个零。
现在、我们接下来要做的是、I SWE 将使用此 ZTK 脚本。
请记住、这是 一个显示极点和零点的函数
信息作为数组。
因此、这将告诉我们 分子是什么
分母是相同的。
这将显示 极点和零点。
此时、您 可以看到存在问题。
因为 这里有一个阻抗极点。
一个极点位于 S 等于 sminus 1、另一个零点
时间极点开始。
据说这 是一种微不足道的认识。
现在、我在这里看到 一个 TA 相当简单的系统。
系统会变得更 复杂、
订单数量众多。
找到这些东西有点难。
有时您不需要 转至传递函数
以查找它们。
但很高兴 MATLAB 为您提供 了一个名为 minreal 的脚本。
看到、 MATLAB 花费多少钱-花费多少钱是惊人的
MATLAB 工作将从它中取出。
MinReal、您将为我提供 传递函数。
在本例中、G1是 ZTK 形式、然后是
将返回 rtransfer 函数、
控制器,即这里的 EC。
在本例中、它将为 我们移除该消除极点。
现在、我们有 一个二阶的 transfe 函数。
我可以继续 对状态空间进行疏浚
评估它的稳态响应。
现在、我 在做它的方式、你会的
这也是一件事 、就是回来
这些系数数组进行比较
该设计的链接。
这与该 TS 数据不相关。
它返回枚 举符和分母的数组、
将系数转换为数组。
然后使用 TF 到 F STO 返回另一个方向。
将函数 转移到状态空间、
它将这两个数组作为 对四个矩阵的返回值
空间描述中所需的所有信息。
我们可以开始了。
现在有 了秒序系统
以国家空间形式表示、 这是一种最小的实现方式。
最后一件 行李简单地确认了
我们现在处理 的是可控和可观察的
转换器。
它与 之前应用的测试 SWE 相同、
构建可控 性和可观察性矩阵、
并在 本例中检查它们的侧面是否为2。
因为 系统的顺序减少了1。
我们可以开始了。
2是 系统的 orde r.
我们有一个2 x 2矩阵、其等级为2。
这是可 控制性矩阵。
因此、我们仍然很好。
现在是可观察的 Matri 坐标轴2 x 2、它有一个秩。
现在、我们也开始 了可观察性。
因此您可能会遇到问题。
这些问题往往 会降低可控性
简称 WCT。
因此 、我们在本次课程中几乎没有遇到过这种情况。
然后、我们将 准时地点餐。
现在、我要在 GTO 中使用的系统非常一致
今天下午 、对于教程、
是一个机械系统。
它基于像 这个这样的双重 sma 系统、其中
有两个质量、M 1和 M2、它们在坐着
并在 某种情况下自由滑动。
因此、您可以想象 这两个质量
金属块或桌子上的某种薄格。
我们可以影响 他们的立场
从 质量 M1的黄昏开始。
当我们这么做时、 很显然 M1将移动。
其位置称为 Y1。
当它移动时、它会 在 M2上施加力、
因为它通过 该弹簧减振器与它耦合
组件
现在、这些 sprin gand 风门值
耦合的情况
耦合非常轻微潮湿。
这意味着、当你在 M1上给它一点细微差别时、
M2将 像这样进行归零、
它将在很 长一段时间内继续执行 lik ethat。
因为 那里有非常轻的阻尼。
那么、现在、如果我构造 它的 da 模型、
就像这样、这可能 会永远地滑动。
因为 没有什么东西可以阻止它。
我所做的是、我已经对 DIN 进行了几个摩擦术语的说明
因此、我 当然不会
你知道 会有摩擦。
这种化石 正在发展
死机有两个原因。
一个是 因为它有点潮湿、
另一个原因是 存在滑动摩擦
这 将最终在这两个质量中获得成功
为了平稳的停止、我 只需给它一个踢。
现在、我 想变量 o finterest 是 Y2。
我想我 在这里的工作就是我
力控制、 施加到 M1的力、
希望专家组 Y2 在我希望的位置。
当然、在 不受控制的无反馈中
情况、某种程度的操作 计、实际上是死算。
但 您将在今天下午晚些时候看到 Ron
控制的应用、
它是令人惊叹的超精确度
使用 gof M2的位置、即使有
它们 之间的间接耦合、
它们之间的轻微阻隔耦合。
现在 、我选择它的原因是
您可以将 此处发生的情况可视化。
它 有一个很好的统计器空间描述。
我将此作为新 版本的书中的附录。
它还可以从 网站下载
附录。
因此、如果 您访问网站和您
查找 该书的版本、
如果您不 想购买这本书、
您实际上可以在 此处重新创建附录、
附录 E、它实际上为 您编写了所有这些内容。
这是 PDF 格式的电子附录、
欢迎 您下载。
而不进行详细 介绍
是运动方程。
这就是这个空间方程的样子。
这是二阶的。
您有 一个4x4系统矩阵。
什么 情况下发生呢?
太好了!
[INAUDIBLE]?
抱歉。
您在附录中给出了它。
这里有一些 mor 电子信息。
我能不能事后跟你谈谈这件事吗?
因为我没有 完整的推导
而设计。
这将有所帮助。
是的,可行。
是的。
我可能应该这么做。
我还没有完成 整个推导过程
而设计。
但方程 中的"sher"几乎是正确的。
它们 不是完全正确的原因就是这样。
我也可以告诉您。
看到、我刚刚应用 了牛顿的第二定律
以获取这两项。
这里也有一个摩擦力。
因为这是 关于运动的电子方程
第一个质量的值、其为 输入力 u
其中涉及的内容。
我已经将 状态指定为
第一 块块块块块块块块的位置及其导数。
那么、这是第一 个质量的速度 DOF、
以及 secon dmass 的位置及其导数。
因此、当我为 x2点形成电子方程时、
乘以加速 因子 nx2点等于所有该批次。
问题是 这里的 mas sterm 出现在左侧。
因此、您将会遵守 这些其他条款
乘 以 M1除以除法、
左 侧有 x2点、如果您愿意、
控制器,即这里的 EC。
而薄 的 gthat 出错了
我忘记 了将该项除以 M1。
那么、在 这里的方程上、这不应该是1。
这应该是1除以 M1、对吧?
因此、无论如何、我在 六个月前发布了该内容。
我了解 了这种情况的结果。
因为有 七或八个像
附录 E 中的不同部分和所有拓扑。
我们的到来 非常漂亮。
然后我开始了 BAC KTO
在我发布了 Dar ning 之后、我查看了它。
天哪!
我忘记了 M1。
您知道 我为什么要离开它?
因为 M1是1千克。
因此 、我在人生中有一次很幸运。
因此 M1是1千克。
好。
现在、让我们快速 学习本教程、
您将看到该 系统的行为、
或没有行为、具体取决于 您的行为定义。
好的,
好了。
所以、我们要做的 是非常精细的非常细化的 gery。
我已在脚本中更正了它。
在这里、我们将使用 SS 函数创建模式焊盘
以创建状态空间模型。
就是这个。
现在、我要做的是 执行模式分解
就像 我之前所做的那样。
我们将看到 模体的外观。
现在、它是一个拥有 一整套特征器的系统。
因为我 现在有一个完整的对角线模式矩阵。
但您已经可以使用 这两个特征值
非常复杂。
因为大多数 esmall 实际组件、
但想象中的分量 非常虚幻。
因此 、您在这里有一个较低的振荡。
我们可以 从中看到的
在第三种模式下存在一个非常小的数字。
这可能意味 着系统不稳定。
但这并不理想。
这低至 MATLAB 的分子分辨率。
这是一个0 eigenvalue。
我们有一 个模式线性输入矩阵
它包含一组复杂的术语。
因此、我 可以控制系统、这很好。
您可能会想象 它是什么样的系统。
和模型 outpu tmatrix 类似
一个复杂的术语集。
因此、它也是 一个不可伺服系统。
到目前为止一切顺利。
我们可以像 以前一样,以同样的方式来核实这一点。
那么、让我来证明 它是可控的
它很复杂。
现在、我要做的是 不执行初始条件
评估它的稳态响应。
我将从 x 矢量中转到 t*、它
因为这里有 四种状态。
我将从 该状态中提取第一状态和第三状态。
现在、我已经在其中添加 了这两者之间的初始分色。
因此、这个 y0 更远、
这表示初始 化两个质量
被距离隔开。
我想我使用 大约一个仪表。
它是一 个非常好的双系统、这个。
那么、当我将其添加到该位置、 然后减去第一个
从第三种模式 中、我从 Y2减去 Y1、
并添加初 始偏移。
因此、这将为 LME 分色
质量的影响。
当我运行它时、 您会看到 EIT 是一个振荡系统
确实。
这是一个曲线。
但您将 看到它会下降
我们开始控制它。
总数值非常高。
因为你给了我 一个微移、它将会运行
就像那样。
这就是 EN/UVLO 引脚。
让我 第二次运行 BAC KA、然后向您展示
我使用了什么初始条件。
这个矢量、我在这里 对第一个位置质量进行了调节
稍微偏右一点、 这是一个正向。
第二个是 左侧的易碎位。
因此、我稍微压缩了一下 sprin GA、
然后放开。
因此、这 种平装的东西压缩了它
为 10 伏或类似的电压,
它会停止所有该运动。
这是 IC。
现在、我们将绘制 单个质量位置。
这是 所涉及的绝对的排列。
因为我 将 Y2的开始考虑在内。
Y0被添加到 Y2中。
在 我们应用该测试时、您将看到行为是如何的。
好了。
那么,这是 ROM。
它要重得多、 而且它的 SGOT 是一个更大的摩擦
大电压系数引起的。
它的 衰减速度非常快。
这是质量 M2 、它受到影响
到更大的程度。
很好。
这 两种情况下会发生什么情况
会在 该幻灯片上缓慢地摆动
Way:
他们在 幻灯片上进一步休息了大约法米
比他们开始时要好很多。
因此、我想您可以通过 执行 BOOING 来实现这一目的、就像这样、
它将 稍微振荡一点。
然后它最终进入 GTO 移动并休息。
就是这样。
如果 我们有如此倾向、
构建该图的波特图。
为此、我们启用 了传递函数
表示
好,就是这。
现在、这证明 存在 SAN 集成。
因此、极小 的 leigenvalue 为0。
然后、我得到 了共轭偶极
和 一个实极点和一个实0。
所有这些东西都可以 在波特图中进行初始化、
样子的拓扑。
因此、我们有一个积分器 、负90度、然后
有一 个共轭共轭极对、它
提供了这个和那个。
然后、这里有一个极点、 真正的极点和一个真正的0
在这里的某个位置。
这些是校验器的校验器。
我们将 更详细地进行检查
此常见问题解答
现在 剩下的是唯一一个细牙
是我最喜欢的部分 、即测验。
类似 矩阵有什么共同之处?
它们相似吗?
因此、它们 是通用的。
[INAUDIBLE]?
是的、它们确实如此。
是的、它们确实具有 名称值的数量
帧周期和帧数。
这不是 我要找的答案。
但这是一个很好的答案。
我 要寻找的答案是他们
用 二表示 Sam 的系统化
不同的坐标系。
但 你绝对是对这种情况的。
在过去,这主要依赖串行总线
模式表示法的两个优点。
我想此时--
简单
您是对的、简化。
从输入 和输出到输出的路径
可视化效果要明显得多。
[听不清]
对,是的。
因此、由于 我们刚才所说的第一个属性、
证明其正确性。
可观察性、 以及可检测性
10K 欧姆的电阻器。
所有这些东西 都更容易实现可视化
在构建 可控制性矩阵时、
例如 ,寻找一个排名。
因此 、对这些内容进行视觉化要容易得多。
对于离散时间系统、内部稳定情况如何?
[听不清]
您处于稳定状态。
说得对。
稳态输出。
因此、内部稳定性、请调用 另一个名称。
Michelle 知道、它具有 有限的输入、有限的状态。
那么、只要输入受 限、状态是否受限?
如果是、它具有边界 输入受限状态、
或内部稳定性。
这种离散时间会怎么样?
那么 CMTI 呢?
我们对系统的看法是什么
它是否具有内部稳定性?
对我来说、内部稳定性确实 是一个错误。
输入怎么样呢?
稳定。
特征值必须是什么?
[听不清]
对。
它将小于1 、或者如果它具有 Lyapunov 稳定、
它必须是 Equa LTO 1或更少该1。
是的。
系统是什么时候- 我刚才告诉过您。
离散 时间系统何时稳定 ISL?
还记得这是什么意思吗?
从 Lyapunov 的角度来看、它是稳定的
当 eigenvalue 剃须一个幅度时
大于或等于 1
因为实际上严格地说 是 Lyapunov 稳定性
还包括渐近 稳定性。
我们如何确定 给定的状态空间
是否在工作。
我为您提供了两种方法。
第一种甲基甲基甲 基甲基甲基甲基甲基甲基胺
模式分解。
我们对铁蛋白模式分解有何看法?
[听不清]
是的。
是的。
模型输出 Matri x 中没有0列。
模式输出矩阵的每个列、
它们是伽马1、 伽马2、伽马3。
每个伽马耦合的对流二极管都朝向输出。
因此、只要这些 gammas 都不是0、
你知道所有 的表情都是通过耦合的。
因此 系统是可以观察到的。
还有一个测试。
[听不清]
是的。
您构建了 可观察性矩阵 Q
它是 C 转置、 转置、C 转置、
这些分区。
它应该具有 N 的全排名
观察性矩阵。
因此 、有两种不同的方法来确定它。
太棒了。
如何观察 可控制的规范表单
相关
我要找一个词。
双性。
它们是彼此的双重结构。
我 通过转置将系统矩阵相关联。
可见的系统 mmatrix、OCF 矩阵
是 CSF 系统矩阵的转置。
然后、您有 可控制的 B 矩阵
是 C 矩阵的转置、
观测 用例、反之亦然。
是的。
可观察性是 我一直在寻找的字。
我将为您提供该值。
QFN/SON 是什么?
它是什么?
它与 状态矢量的大小有关。
它只是 一个具有最小尺寸的系统
向量的
这就是它的样子、 换句话说、就是很大的尺寸。
与 FRAM 有什么不同?”
和 ARM™
[听不清]
是的。
那么、可检测性-是的。
我知道您的意思。
解决了可检测性问题
不稳定模式。
这意味着您可以 通过观察来检测不稳定性
输出端发生的情况。
现在、我们将 花一点时间吃午餐。
但在我们这么做之前 、我要感谢您
在 过去三小时内引起您的注意。
因为这是一项艰巨的工作。
它似乎很抽象。
其中许多是数学运算。
它看起来不像我 在做任何真正的事情。
但今天下午 、请回来。
因为我们 将获取这些信息
要控制双质量系统等系统、
飞行控制器等令人兴奋的东西。
我们以 非常真实的方式使用该信息。
所有这些东西对于 今天下午的到来都很重要。
因此 、对于那些从 TI 外部加入的引信、
我们在回退时看到了一些袋子
吃午餐。
我们将 在1点处恢复、
请重写 第7章。
线性系统的属性 、那么我们的介绍 熟悉 我们的房地产空间配方、 以及我们如何从中提取认证 信息、 包括矢量 和矢量值、 然后是动态 响应 之间的连接时, 优先考虑 MOSFET 表示法和 transfe 函数表示法。 该段 会进一步变小、 并检查 状态空间公式的属性。 尤其是、 非常重要、还有几个 想象 不到的其他人。 最不可避免的属性 是稳定性。 您可能会看到非常清晰的图像 我所说的稳定性。 很明显 、对于稳定的系统、 对于连续时间系统 、甚至是传递函数 稳定意味着什么。 您在看到它时就知道它。 它要么 是一个细长的 gthat 仍然绑定、 或者它不 会重新绑定、这很好。 但对于 stat 空间描述 其中我们有一 个内部变量、 稳定性分为几个级别 认知很重要。 当您进一步讲德语时、 如果您继续了解双头螺栓 非线性系统、 你会发现稳定性确实 是一个非常可怕的概念。 有这样的系统 外观 就像它们是稳定的、 看起来就像它们一样 同时在重写。 因此,我需要从 国家的角度解释稳定 空间说明, 特别是从状态开始 CEO 观点 然后,还有交流损耗。 这些是对资产空间描述的唯一性。 这些称为可控 性和可观察性。 它们不适用于 etransfer 函数描述。 但它们确实适用于 空间描述。 它们非常重要。 因为当我们稍后使用 进行设计控制系统时 状态空间模式、即系统 无法控制、 我们的努力将是徒劳的。 稍后 、当我们开始设计时 估算器或观测器 、这是相同的、 如果无法 观察到我们开始使用的系统、 同样,我们的努力 也是徒劳的。 我们无法从 无法观察到的系统估算 estat。 控制能力 和可观察性 是 我们稍后需要的重要属性。 现在、事实证明、稳定性 以及可控性 和可观察性、 所有这三项 如果 我们可以执行、就会有非常清晰的可视化效果 特定的近亲 DOF 变换 在系统上调用 da 模式分解。 我将向您解释 一下实际的模式分解 方法。 但是、如果您可以执行 eout、则会执行所有这些属性 您会非常清楚、 并且有好处 也是如此。 因此、我们将从 模态分解开始、 我将向您展示 所介绍的属性 以及 其他方面的术语。 然后 、我们将再次查看标准化的实现。 我向您展示了一 种、phas 可变规范形式。 事实证明、它 是另外两个被称为的位 可控制的规范形式 和可观察到的规范 因为此处是三角波形。 这就是为什么这个部分 恰好出现在那个部分之后 控制 能力和可观察性。 然后 是我要做的最后一件事 这 是一个 fairl yshort 部分、 最后要介绍的是冲头 下一个教程、我 将会或多或少地 每个教程都 将基于该教程。 它是一个双质量系统。 它由一 个有两个质量的机械系统组成 耦合在一起、 这样当你推动 水体时、其他质量就会移动。 但 两者之间存在某种能量交换 质量。 结果是振荡。 这是一个很好的、易于视觉化的系统。 它具有很多动态特性 让这些教程 变得有趣 这三种运动。 所以,我要启用系统。 驱动 ZVS 转换。 现在、我想先 解释一下这个概念 矩阵。 当矩阵使用 dfor 变换时、 您已经看到 、在 n 维度中、矩阵具有尺寸 n 乘以 n 矩阵为方形。 因此 、如果存在转换 在 三维空间中、从一个矢量到另一个矢量、 变换矩阵执行 三维变换。 例如、在这里 、我们有一个矢量 V、 它不由矩阵 T1运行 将矢量 t oa 变换为不同的矢量 V tilde。 因此、V tilde 是指向 不同方向的点 Gin 因为 它是由矩阵 T1进行操作的。 现在、T1、如 Wel las V 和 V tilde、 将以该坐标系的项 s表示 或者二者都是复数。 例如 x1、 y1和 z1、它们 可能是正交坐标 它代表矢量 和变换 权衡关系。 现在、让我们想象一下 、我们什么都不会改变、 但所有 这些信息都是坐标系 演示。 我们不使用 x1、y1、z1、而是使用 x2、y2、 Z2. 嗯,现在,相同的 tw omatrics-相同 的两个矢量 具有 slightl ydifferent 表示法。 因为它们的元件 将会不同。 因为它们 虽然指向相同的方向 从理论上讲、它们 在中重新呈现 不同的坐标系。 以及变压器 矩阵 从 V 移动到 V tilde、 这也会有所不同。 因为它的协调 帧发生了变化。 它在做的是相同 的事情、 但它是在 adifferent 坐标系中执行它的。 矩阵 T1和 T2 试用相似的矩阵。 它们可以实现 相同的变换、 但它们在 adifferent 坐标系中执行它。 它们与 所谓的旅游相关 相似性变换。 具体而言、T2 i 序列到 M、再到-1、 T1乘以 M、其中 M 是 相似性变换。 它将 Matri x 从一个坐标系变换 另一个坐标系。 且在 500 MHz 下,其 IP3 为 [听不清] dBm 时 不是吗? 您可以看到矩阵 M它必须进行测量。 它必须具有 与 T 相同的名称尺寸、 因为 T2的 esame 尺寸与 t1相同。 但是、当 你看到它时、M 乘以-1、 考虑相似性变换。 它将在 一秒内进入 com ein。 请注意,这是一个重要的属性, 那么、让我 花几分钟时间来讨论它、 难以仿真。 可以找到类似 的变换矩阵 M、它 采用 T1并使 T2对角线。 如果您可以 执行该操作、则会出现该情况 是 产生的许多好处 系统的电感。 该特定坐标系。 但 为了实现这一点、t1 必须具有一 组完整的特征。 否则、您可以 对 T2进行 tdiagonalize。 如果 T1没有一 组完整的特征向量、 您不能具有对角线 T2、 但您可以接近它。 出现的仿真形式、 称为 Jordan、用于 mrepresentation 稍后我会介绍。 但现在让我们想象一下,我们 已经不会有一整套特征的特征 这种 SoM 相似性变换可以实现 从而 使产生的 diagona lmatrix t2 该矩阵是对角线、bit 具有更进一步的属性 即您可以 对元素进行范围内的操作 对角线 Matri 的斜线、使其如此 以及系统的效率。 类似 的转变 这对你来说是一个 scolumns,它们本身就是这样 T1的特征向量。 这里有一些重要 的信息 一些特性。 如果 T1具有一 组完整的特征向量、 矢量 是定义的 CPU 独立 这些矢量 扫描用作列 以形成类似 的变换矩阵 M 因为 您知道、对于尺寸来说是可以的 你 有 n eigenvalue sin t1、t1是 n x n、 并且 您已经设置了完整值。 您有一个特征矢量。 每个特征都对 RHAS 中的元素感到羡慕。 因此、通过将这些列、 即 M、M 的列进行设置 尺寸也必须为 n b yn。 并通过使用 Matri x 实现相似性 变换、T2斜 线对角线、但不仅仅是 对角矩阵 T 1的特征值将是元素 对角线的对角线。 现在、在 我们了解该信息之前、 我 将向您介绍如何操作 您 可以使用状态方程进行状态变换。 现在、假设我 将一个状态方程式进行了打字 对于基于 关节状态选择的系统 影响。 我之前告诉过你 ,没有什么特别的 状态元素。 大家想用什么都可以。 那么、让我们假设 您做出一个选择、 它对 您来说并不是很有效、 您希望将它们更改为 不同的元素集。 没有理由不能这样做。 变化可能 会因所发生的事情而产生 称为状态变换。 那么、假设您使用的是 x 、并且您希望进行转换、 改用 v。 vis a different -- 我是说它是一个状态矢量、但 我现在将其称为 v。 它与 x 通过 这个矩阵 M 相关、即 现在是 n 的任意矩阵 那么、我们要做的是将 这个直接置于状态 等式、x 点等于 x plu SV。因此、左侧不是 x 点不再出现、但它是 M 时间 SV 点。V 点是新状态 等于 AMV。 MV 只是插入之前 的 xwas,加上 v 乘以 u. v 不变。 现在、我们要做的是 、我的 SWE 将对两侧进行预乘法 与 M 的倒数相反、如果 您可以的话、现在这是一件好事 M 由特征向量组成。 因为 M 肯定 会反向。 因此、您可以 从 M 中找到反向 它是正方形的、因此尺寸 是我们所需要的。 爬虫 程序会以 M 的倒数进行预乘、 您得到 v 点等于 m t othe -1、乘以 M 次 五、看,类似 的状态转变 矢量。 加 n 到-1 乘以 v 乘以 u 我们执行 了相似性变换 在电压矢量上的优先权。 并猜测 负1 AM 矩阵的 MTO 值 变为负数的区域。 它就是带宽。 它 将在前导代码中具有该 eeenvalues 对角矩阵 我们要将其命名为 LPO。 让我们将 M t othe -1B、B1称为。 现在、这是状态向量 Rinto 转换状态。 我们现在需要集中讨论 输出方程。 可以执行相同的操作。 但它要简单得多。 因为我们不会 将 ETO M 反转。我们需要的一切 将 x 替换为 M 时间 SV。我们将其称为 C1。 因此、C Time M 将 变为 t obe c1加 v 乘以 UD 不受所有这些影响。 那么、现在我们有了 stat 公式和输出 该 新状态的 I nterms、v、 v 恰好是多少。 现在、独特的选择 -那么、这里有 无限选择。 您可以随意选择名称。 因此、我们不会将任何 特定状态绑定在一起。 您可以在 一个和另一个之间切换频率。 但对于这种声波 ,v 的元素 有一个特定的名称。 它们被称为 系统的表情。 典型系统运行 I nCharacteristic Set of Patterns、 梯形脉冲。 这些模式称为模式。 它是 状态矢量的电子元素的唯一选择 这些称为模式。 这之所以很 重要的原因是 您将看到 每个模式的时间 与所有其他模式完全解耦。 这种变换、 独特的变换 其中您使用了 eigenvector 列的 Mmatrix 转换为-使用 我的 neffect 矢量变换。 这称为调制 分解。 在以后您了解到 自己可能希望 第一个是 、事实上这些模式是不耦合的 彼此之间、可 提供非常清晰的可视化效果 放大数模转换器和输出之间的信号。 不仅是这样、而且通路 从状态中的输入端 到输出 的状态要清晰得多 如果 你刚刚采取随机状态、你会更好 矢量 MAPS 动态特性 更易于解决。 因为存在 标量、而不是矢量。 您可以对 随时间变化的运动进行非常简单的视图、 它使 系统的动态变得更加清晰。 因为通过公开这些 值、 您知道哪些是主要模式、 这一点不太重要。 请记住 复平面中的电子滤波模式、 复数中左侧的特征值 比 那些衰减得多 在右侧、它们接近 虚轴、 如果它是一 个持续计时系统、那么它们就会被执行 与我 FIT 的离散时间系统并联。 您还可以 获得更清晰的见解 介绍了 tw 属性 更早的可控 性和可观察性。 我 认为通路暴露在外的原因 实现平衡。 该过程在 一段连续的时间内类似 奈奎斯特路径。 只是曲折 的特征值是不同的。 那么,让我们来执行它。 我们将编写 模态相似性变换 我 现在将其称为 W、 因为它是一 个非常具体的转换矩阵。 M、但 我想将其称为 W 由 列 sof W 组成 独立 的特征向量的特征向量 矩阵 A。因此您不需要 对列进行调整、 每列都有 n 个元素。 这是一个 n x n 矩阵。 我将为 该矢量添加符号 因为经济转型也是如此具体 以及 称为模式的独特选择。 我将为 符号 q 进行 E过渡期、 元素 wil lbe Q1到 q sub n 有 系统的模式。 是的。 就是这样。 现在 、存在 r表示 法变化 我想让您知道。 这是 EMI 滤波器部分。 这里是 输出端。 因为这 是一个独特的选择 的列数 W、正如我说过的、我们最终得到 了一个令人激动的新系统 矩阵 DMS 这是一个交流电机。 Lambda 将沿其前对角线包含 A 的特征 那么、写入这些方程 、Iguest 这就是它们的外观。 扇 出的模式矩阵包含在其列中 A 的特征向量 和频谱矩阵、 因为它称为 Lambda 、所以我对角线矩阵在这里 特征值位于 主对角线上、 所有的 释放都是零。 模态矩 阵 是应用 于这两者的名称。 现在、模式输入矩阵是 W 到-1乘以 v 我们将把 W 插入 状态变换公式 那个方程。 我已经解释过的 λ。 现在、输入矩阵 、W 至-1 v。当您 进行此分解时、 将 该输入的各个行分开很有用 矩阵。 因此、我一直将这些行 称为 sbeta 1、beta 2 至 β n 这些是 WTO 的负1 v 行,即 为什么我这么写。 可以将其视为变量。 但实际上 、它们是行矢量、 现在、输入矩阵的第行中有 n 个。 输入 矩阵的 Beta 1和 beta n ar ethe 行、 W 至-1 V 因此、这会 影响您的状态方程 看起来像完整格式。 左侧的模型矢量的导数 等于频谱矩乘 以模态矢量、加 然后、这些是 新模式输入矩阵的行 s. 但我想它们是 一个矢量乘以输入矢量。 如果您愿意、它 将为我提供测试版 捕获所有 电子输入到特定模式的耦合。 然后、Lambda 我捕获 从 Qi 到 Qi 点的动态。 那么、您现在看到了我的意思、即完成 去耦。 如果您可以用 此表单编写 estat 公式。 那么、这是模 态输入矩阵。 这就是它在 到达单个模式时的外观 您得到的方程。 那么、现在请注意 、这个 Lambda 我出现在这里、这是 是完全标量。 关键点是 动态不耦合。 输入矩阵。 现在、模式响应、之前 的每个状态派生 可能涉及 所有其他状态。 因为 状态矩阵可能有一个 da 行 它 一直具有非零元素。 但现在你得到的是我 只需一个一阶 差分方程、 涉及相同的模式。 其他模式不 会产生任何效果。 这是模式的分辨率。 因此、它是用来 修复瞬态响应的特征值。 这将为您提供 模式演进的增长或衰减。 然后、参与 积分涉及 β I 这样我们就可以 得到响应的整形 是 确定该值的矢量 通过 与 B.的关系 输出矩阵 I sthe 乘积为 C 和 W 这对我的想法很有帮助 作为 单独的向量。 此外,可能会发生击穿,这可能 因为该 wil 向上乘以向量。 因此、伽马1至 GAMM an、单独的矢量、 每个矢量对 成个单独的-一种单模式 所有输出上。 那么、这就是我 应该看到的样子。 我是说它们是向量 、但考虑它们 现在至少是标量。 正如我所说的、每个伽马我 都会闪烁一个特定的模式 所有输出上。 以便输出矢量 等于所有这些乘积的总和。 因此伽马1乘以 Q1、plu sgamma 2乘以 Q2、依此类推。 现在、我认为这个图 将把它全部绑在一起。 因为这是我们 所做的所有图形。 我们已更改了显示方式 完全 独立的套件 状态、每个状态 都是完全的 去耦所有其他的。 现在为 729。 因为 Qi 取决于 y 点、反之亦然。 以及空间与所有输入之间的耦合 由相应行的低确定、 输入矩阵的输出。 以及所有输出之间的耦合 由模态输出矩阵的 I colum n 决定。 那么、您现在可以看到吗? 您已经获得了非常清晰的可视化效果 所有输入 如何影响一种模式、 以及 MOD 如何影响所有输出。 这 种表示非常明显 发生的情况。 现在一切都正常、 前提是您已经完成了 一整套 eigenvectors。 如果您没有 、那么您可以使用的单向方法是这样的 如果您使用 了树形特征值。 那么、在我向 您介绍如何操作之前 您使用这些 信息来描述 我 想要的属性 o fa 系统 简单地轻触一下 、如果您有问题、会出现什么问题 有一个去生成系统矩阵。 它只能通过 反复的特征值来实现。 即使这样、我 也可能不会发生。 你可能会幸运 、可以说、你已经成功了 才会出现退化。 但您仍然有 一组完整的特征矢量。 或者您可能运气不好 、丢失一个或多个 铜。 因此、系统会发生退化。 当您遇到 eigenvectors 时、您必须 如果您要执行 TA 模式分解、 您必须 替换 mby、替换缺失的 具有 被调用的矢量的矢量 广义特征向量。 这些 仍将是真正的特征矢量的正交。 但它们不会 满足矢量的要求 我 在前面展示的公式、它是什么 是负 λ i、乘以 WI。 我们寻求 了一种微不足道的解决方案。 因此、它们会对 特征去变体进行泛化。 您可以在网站上找到这些信息。 有一个很长的 yprocess 可以找到它们、 我不打算 在今天的研讨会中讨论这些内容。 但一旦找到 了它们、您就可以使用它们 实现平衡。 但频谱矩阵、对 角线 eigenvalues 不再 是真正的对角线。 它 将在斜升对角线中有一些元件、即1。 这意味着电 极二极管不会完美 去耦所有其他的。 将会有一个小的耦合 EBIT 开启。 Matxri 的形式 具有该对角线、 但某些受支持 的对角线等于1。 它们称为 Jordan 矩阵。 矩阵、即 生成的系统矩阵、 或频谱矩阵、其中 有 Jordan 块。 现在 、在时会出现可能的差分排列 您开始丢失矩阵。 但从根本上说 、特征检测器的编号是 实现的最大值 取决于您 的解决方案 获取公式 A minu si 乘以 λ i 再乘以 WI α1α2 = 0。 这就是你发现了这些嫉妒者的方式,你还记得。 你这样做是为 lambda i 的选择 现在、我的 λ 一定 是可耻的、您可能会失去解决方案。 您可能没有完全 独立的解决方案。 您得到的数字取决于 在空空间维度 o fthis matrix 上、A 减 I 次 λ I. 空的 spac eDimension 会告诉您 您 将要获取多少个电子矢量 该特定的 Lambda I. 在本例中、 有一个整数 我叫 calin ghi、告诉你 可用 特征向量的数量 放大器驱动电路。 且 numrbe 介于1、 你将始终得到 1、而 Mi 特定 特征值的多重性。 如果您幸运、您可以使用 GE TA 全套、在这种情况下 你已经得到 了完全不一般的东西。 我们无需担心。 但是 、如果您没有这么做、 嗯、如果 你只有一个、你 需要这些通用 的去 igenvalues、 最后得到完整 的 Jordan 表格展示。 如果 您具有介于1和多重性之间的 你最终 会看到 Jordan Blocks 出现。 频谱矩阵 x 中有特定的块 它们具有1的超级对角线。 但它们并非全部为1。 它们中有些被压入。 让我来向您展示 一个有关这方面的快速示例。 这可能是一 个 Jorda 挡块 与特定的值相关联 具有一定的多样性。 同谋 是数字 对角线上的元件数。 您可以看到 、所有元素都是0、 但这几个除外。 这称为 Jorda nblock 或 Jordan 矩阵。 因为这是唯一的矩阵。 例如 、这里是一个五阶系统、 它具有三个特征值。 这有两个主要目的。 我有两个在-2处 、两个在+ 3处。 这 是一个不稳定的系统、1位于-1。 那么、在这个 scase 中、会出现什么 是 针对负2处的 tw oeigenvalues、 有一个约旦集团 的 kof A。你看到了吗? 它位于对角线上、 因此特征值 XY 尺寸更小。 但我们 需要的广义的 eigenvecto 在那里放置了1。 然后 、对于3、还有相同的细 gg 一个 Jordan Block 出现 在 ghere、对角线上有3秒、 对角线中为1。 然后是单 个特征值 给了我们一个 与它相关联的嫉妒。 因此 、您会在右下角得到一个很好的-1 i 类似情况。 现在、我将执行 一个快速教程、 只是为了向您展示 如何使用模式分解。 一次、它不再是 这些降压转换器的基础。 当 我清除其他一切时、请与我保持联系。 在本例中、我们在教程6.1中 分解-- 我不知道我做了什么。 为此我 道歉、我按下了一些东西 我不应该把 它分解 组成模式。 那么、很显然、这是 一个三阶系统。 我不知道它 将是怎样表现的。 但它显然有两个输入。 因为输入 Matri x 中有两列。 因此、我们有三个状态、 我们有两个输入、 我们有单 输出、因为 输出矩阵 C 的形式。它有一行。 因此必须有一个输出。 它具有 thre ecolumns、因为我们 知道有三种状态。 输入矩阵为0 - 转换矩阵 很抱歉、是0。 它包含两个元素。 因为有两个输入。 它有一行、 因为有一个输出。 那么、让我们分解 成它的组成模式、 看看会发生什么情况。 那么、首先、我们 要做的就是 hthen 使用 与我相同的方法构建系统 之前在 MATLAB 中展示的。 在我们进行 模分解之前、 我将绘制其响应。 我们将看到其 响应变化 模式分解后。 首先、我 将要构建 阶跃响应 、并绘制三种模式。 现在问题是 、这里有两个输入。 那么、阶跃响应 、问题是-原因 它 有两个 Pste 输入。 因为当 您执行一个步骤时、MATLAB 会对 LDO 产生什么影响 具有两个输入的系统上的响应是 有两组结果。 一个是 施加到第一个输入的 ste、 而第二个保持为0。 另一组结果 、当第一组结果保持为0时、 第二个应用 了阶跃输入。 因此 、这里将会有状态图的 tw oset。 它将反映 状态的维度 由此产生的矢量、 状态矢量结果。 我们可以开始了。 仿真结果如下。 上图是 三种内部状态的演变 当我们有阶跃应用 程序 dto U1、U2保持为0时。 然后 、在这里的底部图中、反向是 这些是 随时间推移的状态解决方案 因为 U1保持恒定、 而 nu2施加了阶跃。 现在、我们要做的是 perfor ma 模式分解。 我们就是通过这种方法来连接它的。 此 CLC 只清除 工作区中的任何内容。 这使事情 对我们来说有点整洁。 然后、我 将再次执行 EIG 指令。 请记住、这是 从中提取的特征值。 但当您使用 这两者的结构时 电 容、电容和电容参数 将返回模态矩阵 W、 频谱矩阵 λ。 嗯 、键盘对 lambda 没有注意。 那么、我将使用大写的 L 这是两个矩阵 、n x n、3 x 3 在这种情况下、将返回这些值。 您为其提供系统 mmatrix a、而不是仅提供平衡 意味着不要平衡 特征检测器、 我的意思是,我只是把 电子贸易机会这样做。 没有关系。 现在 、你已经把 W 变为原来的值。你可以 在类似 的变换中使用它 提取模式输入 和模式输出矩阵。 请记住、模式输入 Matri xwas W 到-1乘以 B 因此、我们将反转 W、 并将其乘以 B 我是雅斯特- 嗯、 我将断开它。 因为我很感兴趣、所以我 将行视为向量。 稍后您会看到。 然后、模态 outpu tmatrix 为 C 乘以 W 然后 、OIS 将代表它们 作为电流 LSB。 我们来操作一下。 您将看到 A、B、C 和 D 消失、 我们最终获得 L 和 MIM 0和 D 我不知道为什么 w EDID 不会结束-好的。 好的。 因此、它所做的就是再次为 我提供 A、B、C 和 D。 但这点我 是作为频谱矩阵的点。 这是 以指数值的 gof 表示的 λ 实现平衡。 这就是 EN/UVLO 引脚。 很好。 我想知道为什么它会被转置。 这实际上是正确的形式。 我不得不思考 为什么它被转置了。 但这是 输入矩阵的巨大形式。 因为它有两列。 有两种方法。 然后,还有交流损耗。 因为 其中有三种状态。 然后是 outpu tmatrix、模态输出矩阵、 透射 性 nmatrix 仍然为0。 我们现在将 执行相同的操作 我们在 Carrie dout 模态分解之前做过。 我们将进行预设 、并绘制状态。 现在,这是问题所在。 对于这种特定的状态选择、 因为我们有一 个完整的对角化光谱矩阵、 我们现在必须具有完全去耦内部状态。 每个状态 都取决于其自身的状态。 因此、我们得到了等于 λ i 乘以 Qi 的 Qi。 它们耦合在一起。 它是第一 个 orde rdifferential 等式。 这里没有其他东西。 您从过去就知道 、一阶解决方案 差分均衡 呈指数级。 因此、当我们计算 并解决这些问题时 对于阶跃输入、我们应该找到 1减去指数衰减 代码。 我们得到的确实是这样。 那么、这些是状态 、以及它们现在是如何演变的 变化情况。 因为它们 彼此去耦。 您可能会看一下 并思考、嗯、好的。 他告诉我们。 那么、什么。 可能系统也发生了变化。 但我 的观点是、它只是这样 系统实际动态的状态变换 不变。 换言之、 整个系统 无论 我是否表示、行为都完全令人感到羞耻 使用 SoM 耳本选择的状态、 或这个特定的选择。 我将向您展示这一点。 现在,我要 做的是,我要 绘制原始系统。 Y1的图、这是 原始系统的输出。 第二个传感器已经成功连接。 好的、这 没什么特别有趣的。 这就是系统的行为方式。 现在、我在 这里的 GTO 中所做的是、 这是一回事。 我将绘制 该图 Y2的顶部、Y2 是发射 分解的输出。 我 希望、所有这些变化 是该图的颜色。 它应该从蓝色变为绿色、 因为它是同一个系统。 它只是国际 动力学 以不同的状态选择表示。 这就是调制 分解为我们所做的事情。 [INAUDIBLE]? 使用 GA 模式分解的主要原因 从 mthe 输入到输出的路径 更清晰。 该属性意味着 可控性的属性 和可观察性、 可预测性等 更容易实现可视化。 看到 GPIO。 没错,这是问题的关键。 因为它会引导我 了解接下来将要做的事情。 [INAUDIBLE]? 是的、这是可能的。 [INAUDIBLE]? 嗯、它会使 引脚感到它 可能会将注意力集中 在非主导模式。 因此、它可能在这方面有所帮助。 或者您是否希望 简化系统 通过减少它的 orde rof、它可能会对您有所帮助 做出该选择。 因此、我 需要在控制设计方面提供帮助的原因有很多。 [INAUDIBLE]? 是的,确实如此。 [INAUDIBLE]? 嗯、有点像。 对,很接近了。 但我想摆脱 超前和滞后的想法 补偿器、也 是根轨迹的除法器。 因为在 系统中-我昨天介绍过 其中我们使用 doutput 反馈、我们 必须 关闭闭环 特定线路上的极点称为 loci 的复平面。 我们 可以更改的唯一精简 gg 是增益、沿 这些轨迹移动轨迹。 状态反馈控制的一大优势 您可以在 复平面中任意选择您喜欢的任意值 放置极点。 您具有极大的灵活性 接近 的环形极点所在的位置。 您 正在使用的栅极、FAC 而 不仅仅是输出中的状态矢量 好处。 因此、我认为这有助于 推进这一决策过程 极点的选择。 现在、我 将稍后更多地使用该小数位。 但我想 在一段时间内继续保持 kabout 稳定性。 那么,有两种 类型的函数。 在 我们继续之前、我想告诉您、 并了解如何使用它们。 第一个问题是,我们 可能会立即这样做 视为稳定的系统。 这一制度占有 财产 称为渐近 cti 稳定性 这意味着它的状态 i nthe initial condition 随着 时间的无限变化、 将收敛于该 电子平衡点。 因此、这相当于一 个稳定节点或一个稳定焦点 在我 之前向您展示的相位纵向中。 因为这种状态 会跟随某种路径。 这是一个稳定的焦点、 最终会随着时间的推移而出现 它稳定地稳定 在平衡点。 它称为渐近稳定性。 对于什么、有一个字的 ydefinition 这意味着、就 可以在多大程度上取代初始条件而言、 它与 平衡点收敛的事实。 因此、具有 连续时间值的系统 小于0、或者 如果是 rdiscrete time eigenvalue 小于 1的模数、具有属性 渐近稳定性。 现在、在 本幻灯片中、我能不能 做一些看起来 很明显的事情 您很清楚、 这一点非常明显。 因为它稍后很重要。 在稳定状态下 、对于渐近稳定系统、 如果是连续时间、您 知道稳态是 由 T 等于0的 x 点定义。 这意味着 estat 不再改变。 它达到 了它的固件点。 那么这是稳态。 但请注意、如果它是 离散时间系统、 存在陷阱。 因为我 在稳定状态下的意思 是 nex tstate 没有不同 输入和现态。 状态 XK 加 1与 XK 相同。 因此、当你保持 稳定状态时 对于分立式系统 、重要的是 右侧 不再是0。 这将在 我们看设计时再次出现 控制 系统中的稳态的高电压基准。 但我想提醒 您注意这一点 一个重要的差异。 实际上 、这是唯一的一个 稳定部队的差异 时间和 离散时间系统之间的差异。 因此 、稳态定义存在差异。 但无论如何、我认为您 可能[听不清] 想象一下,“那是一 种很棒的稳定。 现在 存在某种稳定性、 它位于 phas 纵向图中 其中平衡 点被称为中心。 一般而言、我 称为 Lyapunov 稳定性。 Lyapuno v컈 뚨 所说的是 如果您将初始 状态从其平衡状态中移位 然后让它运行、 前提是您没有 让它从 该状态转得太远、 它将对 状态进行收敛、 也可能不会达到无穷大。 它可能会保持 在平衡的每一个特征中 不 会在比赛中到达它。 这是 一个系统示例 它具有复杂的共轭 值、如果它是连续的 时间、或单 个转盘上的电子值、如果它是离散时间。 因为这些振荡 是持续的。 它位于边界上、不稳定。 它称为预翘曲。 有时您会看到具有 Lyapunov 稳定性的系统、 被称为稳定的是 Lin 的 Lyapunov 感。 这不是我们担心 的事情。 但术语会不时出现 、尤其是 非 线性系统的应用。 但执行 此操作的系统、在本例中 它是二阶 的、它的相位纵向会是 属于 中心的类别、 它具有利亚普诺夫稳定性。 现在 、绘制了两个车床图 就输出而言, DPWM 模块 2 和 此电路的频率响应。 我将讨论的是、没有 WIS 如何涉及输入。 因为 输入的有效性允许 我们将在 内部和外部进行区分 稳定性 首先、 内部稳定性是 耦合的属性介于 输入和状态之间。 它有时称为边界 性状态稳定性、 或 BIBS 稳定性。 有时、它是回调 式内部稳定性。 因为我们在谈论内部 变量集 称为状态。 提供 RA 有界输入、 状态保持 受限 获得 BIBS 或内部稳定性。 如果您解决 稳定性的均衡问题 主动能量传输。 显然、您正在寻找 外部信号。 以及 外部稳定性 当有界输入仅 产生有界输出时定义。 您具有 BIBO 稳定性。 现在、因为输出均衡 仅是代数方程 涉及到状态、则会提供 有界输入 有界状态稳定性、您会 自动获得有界输入 宽输出稳定性 因为在 该状态下、动态特性仅在那里 但不会相反。 这并不一定是一 个关键问题、因为系统是这样的 外部稳定、 内部稳定。 要确定该值、 您需要确定 状态如何从 内部耦合到输出、 主动能量传输。 您可能具有内部状态、这些状态 会像疯狂的那样振荡、但 不会耦合振荡 到输出 电流、因为存在 是输出矩阵中的0个元素。 因此、内部 稳定性是肯定的 可保证外部稳定性 、但不会相反。 好的, 现在、让我们来了解 一下可控性 10K 欧姆的电阻器。 稳定性概念也 会进入这种情况。 我有她 的 eis 四阶 已 执行模式解调后的系统。 它与 我之前展示的图表类似。 因为每个 表情都是完全的 与所有其他组件不耦合。 输入和 每种模式之间的耦合 由 W 减1 B 矩阵的 sw 行确定、 以及从 EAC 模式到所有输出的耦合 C Wmatrix 的列、这些伽马元素。 现在、 这是 W 的异或响应行 负1 B、因此 Bi 转换器 是非零值和伽马 I 非零、很显然 、tmode 是通过耦合的。 因此、您可以说是 因为输入 耦合到该模式、 我可以影响该模式 来减少输入电压。 因此、我 所说的模式是可控的。 因为 CW 矩阵的相应 gcolumn 非零、当该 模式移动时、它是 某种程度上会影响 至少一个输出。 因此、这 种模式的情绪 观察到的相关事物。 模式1被认为是 可控制和可观察的。 您可以看到我 在这个图上进行了详细的了解。 因为您知道该 异或响应矢量、 Beta 1和 γ 1为非零。 现在想象 一下伽马2为零的位置。 这意味着该模式不 会耦合到输出。 我们无法 通过观察输出来确定 gSimply Q2是否稳定 EOR 为不稳定模式。 因此 无法观察到 tmode。 但由于 β 2是非零、 因此它与输入耦合。 因此我们可以对它施加影响。 这 是一种可控但无法观察的模式。 当 reverse 为 true 时、您可以 看看 模式3会发生什么情况、β 3是零、 但伽马3不为零。 因此、这种模式是不可控制的、 但至少可以观察到。 最后、有一种模式 、它与任何东西都是解耦的。 它是一 种无法控制的模式和一种无法观察的模式。 因此、这些属性 非常明确、 模式分解后、它将立即开始运行。 首先、 正如我说过的、它们的重要性是、 您无法确定 任何相关内容 内部可控性从 传输中循环伺服 功能描述 这些只是 状态空间描述中的属性。 幸运的是、物理 系统 控制 器和可观察的、 这意味着、当您 从头开始构建 astate 空间模型时、 某种系统、 即实际系统本身 那么这里的电压将大于 VOH。 但您的模型通常 包含一些简化 或一些假设、意味 着模型可能不会 具有这些属性。 因此您无法 控制 系统或观测器的型号 您的系统模型。 如果您选择的 stat edoes 具有这些属性、 然后执行 astate 变换 不会更改属性。 因此 、您使用的 wha tstate 选择无关紧要、 证明其正确性。 和可观察性 是系统独有的、 而不是选择状态。 你往往有各种原因使稳定部队有问题。 最常见的原因是您 忘记了有极点 在 您的转账职能部门、您可以在此处取消或取消预订 或 等效的传递函数 说明中有 偏斜极点和零点。 但由于 其他原因、您可能会运行 int oit、 例如、对状态进行明智的选择、 或可能是国家数量。 这些东西也可能会降低 可控性 简称 WCT。 首先是包络。 总结 一下左侧的两张幻灯片 sago IAR。 因为只是很喜欢 动态、 从 输入到模式的连接路径、 β 1和 β 2列矩阵矢量 为 SPI。 Q1和 Q2 与输入进行爬电耦合。 那么,这是一个 RAM 地址。 而系统在黄昏中是无法控制的 功能模式。 但它是具体的模式 2、这是不可控制的。 因为模式2未 连接到输入端。 Beta 2是一个0矢量。 这是 IC。 因为这个 特定的特征值 位于右半平面。 这意味着 系统不稳定、 无论如何、GWE 都无法做到这一点。 因为我们无法 控制不稳定模式的通量。 这种薄 的 gg 可能不是很明显 如果您只需要随机 选择状态变量、 以及完整的可变状态 器描述。 但 它可以避免雪的存在 系统中存在不稳定和不可控的仿真二极管。 这将在稍后引发问题。 因此,如果您 在这里有电阻, 分类是 可控和不可控的 非常清楚。 您只需查看 rnonzero beta i 矢量。 这 是一种查看事物的方法。 还有 一个代数测试 适用于一般情况。 代尔拜 ctest 就是这样的。 您首先必须构建 可控制性矩阵 从现在开始、我将调用 P可控性矩阵 这样。 现在、这是 calle da 分区矩阵。 我想这是 昨天的 Matri x代 数笔记中的内容。 一个分区 Matri xcontains 元素 它们本身就是矩阵。 eis 上的这个特定结构如下所示。 它是 B、A 乘以 B、A 平方 B、一直到 A 到 n 减1乘以 B。让我们细小 它的尺寸。 B、您知道、i n x r matrix。 它有 n 行和 r 列。 a 是方形矩阵。 因此它不会 改变行数 有很多类型。 AB 将 会进行仿真、因此是 n x r 矩阵。 A 平方 B、类似地、n 除以 r 因此每个 分区都是 n 乘以 r 因此 、整个东西中都有 n 列。 您有 n 行、您 有 n 次 r 列 一个示例。 然后、你所做的 是、你看一下它的排名。 现在、请记住 矩阵的侧面 是 最大非零决定因素的尺寸 任何位置。 那么 、对于这个矩阵、你可以得到的最重要的排名是什么? 你不能大于 n 因为它中有 n 行。 它有 n 乘以 r 列。 那么、您有一个输入。 它将 是 bEAN n x n matrix。 这就是 EMC 问题。 如果您有10个输入、它 将是10n 的10倍。 但它不能得到大于 n 的 bigge、因为你 需要一个方形 Matri xto 具有一个决定因素。 因此、你 可以拥有的最大的 RAN 是 n 现在、如果这个特定 矩阵具有秩 n、 系统是可控的。 您是怎么做的。 对于离散时间系统 也可以这样做, 唯一的区别是 电位变化、A 的 C、 B 的伽马。 否则、您将构建 控制 器矩阵、并对其进行评估 完全相同的方式。 您 可以说有 SoM 的表达方式。 如果您只有一个级别 o fv、其中 v 小于 n 然后您知道您 只能使用 v 可控模式。 您有 n minu SV 不可控模式。 因为其中 n 减 v Beta 检测器为零。 还有一些人在可 控制性指数中进行了定义 因为 它是必须具有的最小数量的分区 添加、直到您获得全排名。 嗯、无论如何、这是第三 个可控制性指数。 现在、可观察性非常 相似、令人惊讶的是、 令人震惊的相似之处。 我有一个问题。 请说。 [INAUDIBLE]? 是的。 [INAUDIBLE]? 当然。 [INAUDIBLE]? 好的。 [INAUDIBLE]? 你会说 滴滴不会改变。 它 将永远到达一零。 你们得到的是这个吗? 是的。 就是这个[听不清]。 它将如何激发? 是的。 答案 是、我在数学上讲这个东西 将永远保持为零。 实际上,我们没有这样做过。 存在影响 系统的噪声和扰动 实际上、您只是 不知道。 它不会保持为零。 但你已经确定了你 不能影响它的 FAC 低电压。 因此、无论发生什么 情况、您都无法更改。 什么都不会改变。 因为会 有激发它的 SoM e扰动。 然后实习 YIT 将会增长。 但从数学角度讲、您是对的。 没有什么可以激发它的。 因此、理论上、它 永远不会保持为零。 但这不是必需的。 是的。 这是 ROM。 音频正常吗? 是的。 好的。 因此、继续 观察、 没什么特别的。 我们解决 了可观察性的均衡问题 放大数模转换器和输出之间的信号。 它是 CW 矩阵的列 s 它为我们提供该信息。 如果它们都是非零、 那么-即使是模式 通过输出耦合。 因为 γ 1、即 refxample、决定了 Q1与 所有输出耦合的方式。 在左侧、有 一个可观察的系统。 它仍然是一个不稳定的系统。 因为如果 N 大于 0, 它是一种 弱实时系统。 大家可以看到这一点。 因此、该电子模块 将会振荡。 但至少我们可以检测 输出端的振荡。 这是 可观察性的定义。 右侧是 I hav EAN 不稳定系统。 我认为它具有相同的模式 、因此具有相同的特征值。 但这是不可观察的、 因为伽马2是0。 CW 矩阵的第二列为0、 因此、secon dmode 未连接 任何输出。 我们 没有什么可以检测到什么 第二种模式将会执行。 这 也有一个代尔拜克特尔。 它涉及形成 顶点矩阵 时间反转函数。从现在起、P Q 将为 这两个矩阵保留 dd。 因为我们现在非常需要 GTO。 现在形成 了分区 从 C 转置、转置、 转置、转置 转置等。 您在 该矩阵中查找运行 kof n。 如果您有它、 则可以观察到 nthe 系统。 如果您没有 该系统、则无法观察到系统。 离散时间有一个并行 替换为 C 的系统 现在有两 个相关的附加属性。 其中第一个是 我的扇贝稳定性。 IO_SUP 与 RX_SUP 相同。 但问题是仅针对 不稳定模式。 我来举一个例子。 这是一个系统、它是 一个无法控制的系统。 因为我们知道 FIRS tmode 与输入不耦合。 因为 Beta 1为0。 因此、这个 modeCAN 执行它所需要的任何操作。 w eCAN 无法影响这个模式。 但它是一种稳定模式、 至少它是稳定的。 但是、第二种模式是不稳定的。 但它具有一 个非 Zer obeta 2矢量。 因此、它通过 输入耦合、 因此、w eCAN 会影响它。 我们可以稳定 输入的 b y 操作。 因此、我 可以控制该系统、 需要的电压电平。 但至少它是可以稳定的。 但可以设计它。 还有另一 个与此相同的 mter。 但它会应用于输出。 它称为预翘曲。 它是可观察的、但只能寻址 到不稳定的模式。 实际上、它是 Sam esystem、 但在这里、您已经获取 tgamma 1非零值、 第一种模式是耦 合到输出。 第二个问题是可靠性。 现在、这里的第一 种模式是不稳定的。 因此、它 是一个可检测的系统、 降压-升压解决方案的大门。 第二项要求源于 虽然它不可观察、 因为它是稳定的 则可以说器件具有 ELDRS。 这意味着、如果 涉及到一个 yinternal 振荡、 系统内部任何不稳定的东西、 至少您可以检测到它。 因此、我通过 两种方式定义了可控性和可观察性。 我已经定义了稳定性 和可检测性 是可控 性和可观察性 但仅解决 不稳定模式的问题。 下面我们快速测验一下。 因为这 真的很有趣。 我们将对 结构特性进行调查 四阶系统的性能。 我 没有任何 IDE。 因为我不记得 本教程是如何实现的。 那么,让我们看看两种情形。 首先 、我们创建系统。 这里没有 什么令人惊讶的东西、 仅使用 SS 和 A、B、C、 D首先、我们要介绍 进行稳定性分析。 现在 、MATLAB 中有一个手录。 您不必担心 像 eigenvectors 这样的事情 和特征值、以及在 左半部分计划中的工作情况、 或右半平面。 您只需键入即可保持稳定。 是稳定的、它真的需要所有的东西 、不是吗? 因此、 您所做的是、您键入的是稳定的、 或者它是稳定还是不稳定。 是的。显然这 是一个不稳定的系统。 我们还不知道它。 但它是一种电路外的 EOS。 现在、我们要在 GTO 中做的下一件事是检查可控性。 我首先要做 的是我正在看 显示了片上 SRAM 的大小。 这将告诉你维特 尼-现在如果你在这里键入1、 它将告诉您 行数。 如果您键入2、则 会显示列数。 因为 它们的尺寸为1、2。 但我知道 AIS 是一个方形矩阵。 因此、这并不重要。 这将告诉我 系统的尺寸是多少。 当然、在 本例中、它是4。 然后、在这里、我 介绍了重要的一行、 因为这是 可控制性矩阵的构造。 CTRB 构造 控制性矩阵 您 所需的两个抹香 为其提供 系统矩阵 A、 和输入矩阵 C 因此,我们 现在对 P 退了 我只需要了解 P 的级别 与 A 的尺寸相同、它 是系统的等级 和系统的尺寸。 如果是、 则系统是可控的。 如果不 是、则是无法控制的。 很高兴这 是一个可控制系统。 因此 、在那里的某个地方有一个不稳定的仿真二极管。 但至少它是可控的。 因此、您可以说 该系统是可稳定的、 尽管它不稳定。 现在、我们将为 可观察性做类似的事情。 我将使用构建 可观察性矩阵 Q 为其提供 A 和 C 矩阵、 然后再次检查排名。 希望运行 的 kwill 等于4。 不幸的是、它不是。 等级小于4。 因此 、系统无法观察到。 并尝试 去探索神秘之地 在这个系统的后面、我们 将进行模式分解 你会发现这是为什么。 那么、我们将 共同定义 A 的 EIG 为我们提供一 个模态 d光谱 矩阵、 然后计算调制 线性输出和输出矩阵。 这是下一个脚本中的目标。 我们可以开始了。 现在、在我们 进一步讨论这个问题之前、 一些属性 现在变得清晰。 因为我们所做的都不 是模态分解。 我们显然拥有 完整的一组特征值、 和完整的特征 矢量。 由于所有 这些值都不同、 因此,我们知道我们 不会成为一整套特征的特征。 但是、如果您看 一下它们、左半平面、 左半平面 、你得到的是加1。 这就是 系统不稳定的原因。 这里有一种积极的价值。 3号为正。 嗯、我们知道它是 一个可控系统、 所以 我们不应该感到惊讶 einput 矩阵的所有行都不为零。 但我们也知道我 无法观察到、 这意味着 模式的 SoM eof 不是 噪声有多少。 输出 矩阵的头两列 为0。 因此伽马1和 伽马2都是0。 但伽马3和 伽马4不是0。 我们已准备好 [? 我们有 ISO-21848。 我们有 ISO-21848。 现在、 我告诉过您的其他一些属性 稳定性 和可检测性。 那么、让我们 先处理稳定性问题。 这 是不可扩展的系统吗? 是的。 米歇尔说是的。 每个人都能实现 经济转型的稳定? 它是稳定的、 因为所有模式都是如此 RTI = 参考了输入 因此 、无论模式的音调如何都是不稳定的。 它通过耦合。 因此它 可以稳定下来。 这是可检测系统吗? 为什么没有呢? 好。 嗯,请思考一下。 可检测性是可观察性、 但仅解决此问题 ECG 波形总是延迟。 因此、我们不是处于 稳定模式的中间位置 不稳定的情况。 嗯、它是第三个 不稳定的模块。 因此、我们将提高 可检测性、 可观察性。 我们需要 CW 矩阵非零的第三个色谱。 就是这里。 通过观察 gthe 输出、我们得到了 至少得到 了这个东西的电子信息 变为负数的区域。 这 是一个稳定的电子和一个可检测的系统。 但这并不理想。 这是无法观察到的 、整体来看。 因此 、该系统具有这些属性。 好。 我希望我们几乎就在那里。 我们有两种形式。 我不打算对这个进行人工操作。 因为我已经完成了。 这几乎是午餐时间。 这是 phas 可规避的规范形式。 这两者之间的任何不同之处 我 在上一张幻灯片中展示了相位 变量规范对于 mon、它是标题。 它称为控制 器 ecanonical 表单。 您可以通过 我向您展示的过程来实现这一点 开始, 您会得到矩阵的非常识别的电子结构。 您可以从 系统矩阵中获取该值 其中所有 的不祥因子系数 显示在底部行中。 除 超对角线外、矩阵的其余部分为0、 即1。 这是因为状态的选择、 即状态选择 是相位。 B 矩阵、输入矩阵 、为0、除了最后一个矩阵。 C 矩阵、 输出矩阵、 包含 分子的系数。 当您看到它时 、您就知道您是 处理控制 器 ecanonical 表单。 它称为自动生成该表单 可控 今天 下午、我们将使用这种形式 设计状态空间系统。 现在 、有一个类似的形式、称为 可观察的规范形式。 我将 很快地向您介绍、 告诉你 滴滴的关系非常密切 与可控 性表单非常接近。 该矩阵是 可观察到的规范形式、 现在我将调用 OCF。 好。 您有 CCF 和 OCF、 您可以看到这些缩写。 OCF 系统矩阵 与 CCF 系统矩阵相关 锁存器。 这就是所有的不同之处。 现在来看看关断, 对于观测 表例形式、 输出为 经济过渡期 控制 器规范形式的矩阵、 这两者也与 转置相关。 在某种意义上、可 控制的输出矩阵 是 可观察输入矩阵的转置、 反之亦然。 接下来,请看这里的 观测 表例形式的矩阵、 它与输入矩阵相同 可控制的 canonica lform、只是转置。 因此、如果您了解 一下音调描述、 您已经自动 获得了另一个、 如果您现在有 转置、OCF 和 CCF。 现在、 当我们来到这里时、这些东西令人非常愉快 进行状态空间设计。 CCF 更改了状态 反馈的设计 非常简单。 和 OCF 表格让 观察员设计人员 简单的提示。 现在它们是 calle dcomp配套 表单。 它们通过 这些转置相互关联、 我在 上一张幻灯片中向您介绍的内容。 但是、这种关系我 非常强大、 您最初可能想象的更强大的功能。 这种关系的名称 称为 duality、 这意味着这两个系统 被这些矩阵所描述 相反的信号线。 因此、您可以选择 其中一个的可控性 检测 对方的可观察性、反之亦然。 因为如果您在寻找 P 和 Q 矩阵、 它们的关联 方式与我的关联方式不完全相同。 请记住、P 矩阵是 B 分区 B、A 乘以 B、 乘以 B 可观察性矩阵 I twas C 转置在 B 位置、 和 A 的转置 I nplace。否则 完全相同。 因此、当您检查 其中一个的可控性时、 您实际上正在检查 另一个是否具有可循环性。 这种类似的并行功能有助于我们以后的工作 详述这一点。 因为使用 的技术是这样的 电压反馈控制器的设计 与 您用于观测器设计的完全相同。 这是一件充满力量的事情。 因为您只 能获得一组流程、 您可以执行这两个作业。 在这一部分的最后, 我 将向您展示一个非常简短的教程 可能会出现什么问题。 有一个术语"最低 限度实现" 这意味着您找到 了具有最小空间矢量的空间矢量 可能的尺寸。 以及您的模型可以使用的 GIS 的功能 在那里有状态、什么 都不做。 保存的操作太多。 您可能有 第三阶系统。 但你不小心 给了它四个状态。 当你这样做的时候 ,事情可能会出错。 通常 会出现问题的是您 失去 了我刚才讨论过的一个属性。 例如、您会丢失 可控制性属性、 这意味着 UCA 无法控制系统。 因此、您必须开始 确保已经完成了 具有可控性。 如果没有、请看一下。 您是否在处理 实现问题? 为了说明这一点、 我将执行它 以组织形式提供、教程6.3。 这意味着、对 可控性和进行调查 三 阶的可观察性属性似乎无害 一个输入。 因为 B 矩阵是 acolumn 矩阵、并且有一个输出、 因为 C Matri 坐标轴是行矩阵。 那么、让我们在 MATLAB 中查看这一点、看看会发生什么情况。 因此 、从一开始就没有什么令人惊讶的、 我们将开始 建立这一制度。 命令窗口中没有任何显示。 但这些是 工作区中的 Matrice swover。 我们已经构建了系统。 现在、我们将确定 首先可控性、 使用过去 用过的技术, 构建 可控制性矩阵、 并确定其等级是否为 等于 系统矩阵的大小。 如果是、 则系统是可控的。 如果它不 是-嗯、它是不可控制的。 但令人高兴的是、这是一个。 因为系统 mmatrix 是3 x 3。 这是 P 矩阵。 我们正在寻找它 中的大非零决定因素。 实际上、它会发生 这种情况 具有非零决定因素。 因此 、该矩阵的排名为3、3等于3。 因此、这 是一个可控系统。 现在、让我们继续、为 可观察性做些令人遗憾的事情。 我们已经知道 n 是3。 我们不必重新计算它。 可观察性、这 是可观察性矩阵。 不幸的是、最大 非零决定因素是2 降低了 2 毫瓦。 在这里、它具有2级。 2小于3、这 是一个无法观察到的系统。 现在、为了找出 原因、我接下来要做的是什么 查看 传递函数的 stat 部分。 因此、我将 使用脚本转换 S STO TS 要转换为 transfe 函数描述、 然后 TS 从 它构造 G、即 etransfer 函数。 我们来看看这个。 简单地说、好的、 到目前为止没有什么明显的。 它是一个三阶系统 、其中包含两个零。 现在、我们接下来要做的是、I SWE 将使用此 ZTK 脚本。 请记住、这是 一个显示极点和零点的函数 信息作为数组。 因此、这将告诉我们 分子是什么 分母是相同的。 这将显示 极点和零点。 此时、您 可以看到存在问题。 因为 这里有一个阻抗极点。 一个极点位于 S 等于 sminus 1、另一个零点 时间极点开始。 据说这 是一种微不足道的认识。 现在、我在这里看到 一个 TA 相当简单的系统。 系统会变得更 复杂、 订单数量众多。 找到这些东西有点难。 有时您不需要 转至传递函数 以查找它们。 但很高兴 MATLAB 为您提供 了一个名为 minreal 的脚本。 看到、 MATLAB 花费多少钱-花费多少钱是惊人的 MATLAB 工作将从它中取出。 MinReal、您将为我提供 传递函数。 在本例中、G1是 ZTK 形式、然后是 将返回 rtransfer 函数、 控制器,即这里的 EC。 在本例中、它将为 我们移除该消除极点。 现在、我们有 一个二阶的 transfe 函数。 我可以继续 对状态空间进行疏浚 评估它的稳态响应。 现在、我 在做它的方式、你会的 这也是一件事 、就是回来 这些系数数组进行比较 该设计的链接。 这与该 TS 数据不相关。 它返回枚 举符和分母的数组、 将系数转换为数组。 然后使用 TF 到 F STO 返回另一个方向。 将函数 转移到状态空间、 它将这两个数组作为 对四个矩阵的返回值 空间描述中所需的所有信息。 我们可以开始了。 现在有 了秒序系统 以国家空间形式表示、 这是一种最小的实现方式。 最后一件 行李简单地确认了 我们现在处理 的是可控和可观察的 转换器。 它与 之前应用的测试 SWE 相同、 构建可控 性和可观察性矩阵、 并在 本例中检查它们的侧面是否为2。 因为 系统的顺序减少了1。 我们可以开始了。 2是 系统的 orde r. 我们有一个2 x 2矩阵、其等级为2。 这是可 控制性矩阵。 因此、我们仍然很好。 现在是可观察的 Matri 坐标轴2 x 2、它有一个秩。 现在、我们也开始 了可观察性。 因此您可能会遇到问题。 这些问题往往 会降低可控性 简称 WCT。 因此 、我们在本次课程中几乎没有遇到过这种情况。 然后、我们将 准时地点餐。 现在、我要在 GTO 中使用的系统非常一致 今天下午 、对于教程、 是一个机械系统。 它基于像 这个这样的双重 sma 系统、其中 有两个质量、M 1和 M2、它们在坐着 并在 某种情况下自由滑动。 因此、您可以想象 这两个质量 金属块或桌子上的某种薄格。 我们可以影响 他们的立场 从 质量 M1的黄昏开始。 当我们这么做时、 很显然 M1将移动。 其位置称为 Y1。 当它移动时、它会 在 M2上施加力、 因为它通过 该弹簧减振器与它耦合 组件 现在、这些 sprin gand 风门值 耦合的情况 耦合非常轻微潮湿。 这意味着、当你在 M1上给它一点细微差别时、 M2将 像这样进行归零、 它将在很 长一段时间内继续执行 lik ethat。 因为 那里有非常轻的阻尼。 那么、现在、如果我构造 它的 da 模型、 就像这样、这可能 会永远地滑动。 因为 没有什么东西可以阻止它。 我所做的是、我已经对 DIN 进行了几个摩擦术语的说明 因此、我 当然不会 你知道 会有摩擦。 这种化石 正在发展 死机有两个原因。 一个是 因为它有点潮湿、 另一个原因是 存在滑动摩擦 这 将最终在这两个质量中获得成功 为了平稳的停止、我 只需给它一个踢。 现在、我 想变量 o finterest 是 Y2。 我想我 在这里的工作就是我 力控制、 施加到 M1的力、 希望专家组 Y2 在我希望的位置。 当然、在 不受控制的无反馈中 情况、某种程度的操作 计、实际上是死算。 但 您将在今天下午晚些时候看到 Ron 控制的应用、 它是令人惊叹的超精确度 使用 gof M2的位置、即使有 它们 之间的间接耦合、 它们之间的轻微阻隔耦合。 现在 、我选择它的原因是 您可以将 此处发生的情况可视化。 它 有一个很好的统计器空间描述。 我将此作为新 版本的书中的附录。 它还可以从 网站下载 附录。 因此、如果 您访问网站和您 查找 该书的版本、 如果您不 想购买这本书、 您实际上可以在 此处重新创建附录、 附录 E、它实际上为 您编写了所有这些内容。 这是 PDF 格式的电子附录、 欢迎 您下载。 而不进行详细 介绍 是运动方程。 这就是这个空间方程的样子。 这是二阶的。 您有 一个4x4系统矩阵。 什么 情况下发生呢? 太好了! [INAUDIBLE]? 抱歉。 您在附录中给出了它。 这里有一些 mor 电子信息。 我能不能事后跟你谈谈这件事吗? 因为我没有 完整的推导 而设计。 这将有所帮助。 是的,可行。 是的。 我可能应该这么做。 我还没有完成 整个推导过程 而设计。 但方程 中的"sher"几乎是正确的。 它们 不是完全正确的原因就是这样。 我也可以告诉您。 看到、我刚刚应用 了牛顿的第二定律 以获取这两项。 这里也有一个摩擦力。 因为这是 关于运动的电子方程 第一个质量的值、其为 输入力 u 其中涉及的内容。 我已经将 状态指定为 第一 块块块块块块块块的位置及其导数。 那么、这是第一 个质量的速度 DOF、 以及 secon dmass 的位置及其导数。 因此、当我为 x2点形成电子方程时、 乘以加速 因子 nx2点等于所有该批次。 问题是 这里的 mas sterm 出现在左侧。 因此、您将会遵守 这些其他条款 乘 以 M1除以除法、 左 侧有 x2点、如果您愿意、 控制器,即这里的 EC。 而薄 的 gthat 出错了 我忘记 了将该项除以 M1。 那么、在 这里的方程上、这不应该是1。 这应该是1除以 M1、对吧? 因此、无论如何、我在 六个月前发布了该内容。 我了解 了这种情况的结果。 因为有 七或八个像 附录 E 中的不同部分和所有拓扑。 我们的到来 非常漂亮。 然后我开始了 BAC KTO 在我发布了 Dar ning 之后、我查看了它。 天哪! 我忘记了 M1。 您知道 我为什么要离开它? 因为 M1是1千克。 因此 、我在人生中有一次很幸运。 因此 M1是1千克。 好。 现在、让我们快速 学习本教程、 您将看到该 系统的行为、 或没有行为、具体取决于 您的行为定义。 好的, 好了。 所以、我们要做的 是非常精细的非常细化的 gery。 我已在脚本中更正了它。 在这里、我们将使用 SS 函数创建模式焊盘 以创建状态空间模型。 就是这个。 现在、我要做的是 执行模式分解 就像 我之前所做的那样。 我们将看到 模体的外观。 现在、它是一个拥有 一整套特征器的系统。 因为我 现在有一个完整的对角线模式矩阵。 但您已经可以使用 这两个特征值 非常复杂。 因为大多数 esmall 实际组件、 但想象中的分量 非常虚幻。 因此 、您在这里有一个较低的振荡。 我们可以 从中看到的 在第三种模式下存在一个非常小的数字。 这可能意味 着系统不稳定。 但这并不理想。 这低至 MATLAB 的分子分辨率。 这是一个0 eigenvalue。 我们有一 个模式线性输入矩阵 它包含一组复杂的术语。 因此、我 可以控制系统、这很好。 您可能会想象 它是什么样的系统。 和模型 outpu tmatrix 类似 一个复杂的术语集。 因此、它也是 一个不可伺服系统。 到目前为止一切顺利。 我们可以像 以前一样,以同样的方式来核实这一点。 那么、让我来证明 它是可控的 它很复杂。 现在、我要做的是 不执行初始条件 评估它的稳态响应。 我将从 x 矢量中转到 t*、它 因为这里有 四种状态。 我将从 该状态中提取第一状态和第三状态。 现在、我已经在其中添加 了这两者之间的初始分色。 因此、这个 y0 更远、 这表示初始 化两个质量 被距离隔开。 我想我使用 大约一个仪表。 它是一 个非常好的双系统、这个。 那么、当我将其添加到该位置、 然后减去第一个 从第三种模式 中、我从 Y2减去 Y1、 并添加初 始偏移。 因此、这将为 LME 分色 质量的影响。 当我运行它时、 您会看到 EIT 是一个振荡系统 确实。 这是一个曲线。 但您将 看到它会下降 我们开始控制它。 总数值非常高。 因为你给了我 一个微移、它将会运行 就像那样。 这就是 EN/UVLO 引脚。 让我 第二次运行 BAC KA、然后向您展示 我使用了什么初始条件。 这个矢量、我在这里 对第一个位置质量进行了调节 稍微偏右一点、 这是一个正向。 第二个是 左侧的易碎位。 因此、我稍微压缩了一下 sprin GA、 然后放开。 因此、这 种平装的东西压缩了它 为 10 伏或类似的电压, 它会停止所有该运动。 这是 IC。 现在、我们将绘制 单个质量位置。 这是 所涉及的绝对的排列。 因为我 将 Y2的开始考虑在内。 Y0被添加到 Y2中。 在 我们应用该测试时、您将看到行为是如何的。 好了。 那么,这是 ROM。 它要重得多、 而且它的 SGOT 是一个更大的摩擦 大电压系数引起的。 它的 衰减速度非常快。 这是质量 M2 、它受到影响 到更大的程度。 很好。 这 两种情况下会发生什么情况 会在 该幻灯片上缓慢地摆动 Way: 他们在 幻灯片上进一步休息了大约法米 比他们开始时要好很多。 因此、我想您可以通过 执行 BOOING 来实现这一目的、就像这样、 它将 稍微振荡一点。 然后它最终进入 GTO 移动并休息。 就是这样。 如果 我们有如此倾向、 构建该图的波特图。 为此、我们启用 了传递函数 表示 好,就是这。 现在、这证明 存在 SAN 集成。 因此、极小 的 leigenvalue 为0。 然后、我得到 了共轭偶极 和 一个实极点和一个实0。 所有这些东西都可以 在波特图中进行初始化、 样子的拓扑。 因此、我们有一个积分器 、负90度、然后 有一 个共轭共轭极对、它 提供了这个和那个。 然后、这里有一个极点、 真正的极点和一个真正的0 在这里的某个位置。 这些是校验器的校验器。 我们将 更详细地进行检查 此常见问题解答 现在 剩下的是唯一一个细牙 是我最喜欢的部分 、即测验。 类似 矩阵有什么共同之处? 它们相似吗? 因此、它们 是通用的。 [INAUDIBLE]? 是的、它们确实如此。 是的、它们确实具有 名称值的数量 帧周期和帧数。 这不是 我要找的答案。 但这是一个很好的答案。 我 要寻找的答案是他们 用 二表示 Sam 的系统化 不同的坐标系。 但 你绝对是对这种情况的。 在过去,这主要依赖串行总线 模式表示法的两个优点。 我想此时-- 简单 您是对的、简化。 从输入 和输出到输出的路径 可视化效果要明显得多。 [听不清] 对,是的。 因此、由于 我们刚才所说的第一个属性、 证明其正确性。 可观察性、 以及可检测性 10K 欧姆的电阻器。 所有这些东西 都更容易实现可视化 在构建 可控制性矩阵时、 例如 ,寻找一个排名。 因此 、对这些内容进行视觉化要容易得多。 对于离散时间系统、内部稳定情况如何? [听不清] 您处于稳定状态。 说得对。 稳态输出。 因此、内部稳定性、请调用 另一个名称。 Michelle 知道、它具有 有限的输入、有限的状态。 那么、只要输入受 限、状态是否受限? 如果是、它具有边界 输入受限状态、 或内部稳定性。 这种离散时间会怎么样? 那么 CMTI 呢? 我们对系统的看法是什么 它是否具有内部稳定性? 对我来说、内部稳定性确实 是一个错误。 输入怎么样呢? 稳定。 特征值必须是什么? [听不清] 对。 它将小于1 、或者如果它具有 Lyapunov 稳定、 它必须是 Equa LTO 1或更少该1。 是的。 系统是什么时候- 我刚才告诉过您。 离散 时间系统何时稳定 ISL? 还记得这是什么意思吗? 从 Lyapunov 的角度来看、它是稳定的 当 eigenvalue 剃须一个幅度时 大于或等于 1 因为实际上严格地说 是 Lyapunov 稳定性 还包括渐近 稳定性。 我们如何确定 给定的状态空间 是否在工作。 我为您提供了两种方法。 第一种甲基甲基甲 基甲基甲基甲基甲基甲基胺 模式分解。 我们对铁蛋白模式分解有何看法? [听不清] 是的。 是的。 模型输出 Matri x 中没有0列。 模式输出矩阵的每个列、 它们是伽马1、 伽马2、伽马3。 每个伽马耦合的对流二极管都朝向输出。 因此、只要这些 gammas 都不是0、 你知道所有 的表情都是通过耦合的。 因此 系统是可以观察到的。 还有一个测试。 [听不清] 是的。 您构建了 可观察性矩阵 Q 它是 C 转置、 转置、C 转置、 这些分区。 它应该具有 N 的全排名 观察性矩阵。 因此 、有两种不同的方法来确定它。 太棒了。 如何观察 可控制的规范表单 相关 我要找一个词。 双性。 它们是彼此的双重结构。 我 通过转置将系统矩阵相关联。 可见的系统 mmatrix、OCF 矩阵 是 CSF 系统矩阵的转置。 然后、您有 可控制的 B 矩阵 是 C 矩阵的转置、 观测 用例、反之亦然。 是的。 可观察性是 我一直在寻找的字。 我将为您提供该值。 QFN/SON 是什么? 它是什么? 它与 状态矢量的大小有关。 它只是 一个具有最小尺寸的系统 向量的 这就是它的样子、 换句话说、就是很大的尺寸。 与 FRAM 有什么不同?” 和 ARM™ [听不清] 是的。 那么、可检测性-是的。 我知道您的意思。 解决了可检测性问题 不稳定模式。 这意味着您可以 通过观察来检测不稳定性 输出端发生的情况。 现在、我们将 花一点时间吃午餐。 但在我们这么做之前 、我要感谢您 在 过去三小时内引起您的注意。 因为这是一项艰巨的工作。 它似乎很抽象。 其中许多是数学运算。 它看起来不像我 在做任何真正的事情。 但今天下午 、请回来。 因为我们 将获取这些信息 要控制双质量系统等系统、 飞行控制器等令人兴奋的东西。 我们以 非常真实的方式使用该信息。 所有这些东西对于 今天下午的到来都很重要。 因此 、对于那些从 TI 外部加入的引信、 我们在回退时看到了一些袋子 吃午餐。 我们将 在1点处恢复、 请重写 第7章。
线性系统的属性 、那么我们的介绍
熟悉 我们的房地产空间配方、
以及我们如何从中提取认证 信息、
包括矢量 和矢量值、
然后是动态 响应
之间的连接时, 优先考虑 MOSFET
表示法和 transfe 函数表示法。
该段 会进一步变小、
并检查 状态空间公式的属性。
尤其是、
非常重要、还有几个
想象 不到的其他人。
最不可避免的属性
是稳定性。
您可能会看到非常清晰的图像
我所说的稳定性。
很明显 、对于稳定的系统、
对于连续时间系统 、甚至是传递函数
稳定意味着什么。
您在看到它时就知道它。
它要么 是一个细长的 gthat 仍然绑定、
或者它不 会重新绑定、这很好。
但对于 stat 空间描述
其中我们有一 个内部变量、
稳定性分为几个级别
认知很重要。
当您进一步讲德语时、
如果您继续了解双头螺栓 非线性系统、
你会发现稳定性确实 是一个非常可怕的概念。
有这样的系统 外观
就像它们是稳定的、 看起来就像它们一样
同时在重写。
因此,我需要从 国家的角度解释稳定
空间说明, 特别是从状态开始
CEO 观点
然后,还有交流损耗。
这些是对资产空间描述的唯一性。
这些称为可控 性和可观察性。
它们不适用于 etransfer 函数描述。
但它们确实适用于 空间描述。
它们非常重要。
因为当我们稍后使用 进行设计控制系统时
状态空间模式、即系统 无法控制、
我们的努力将是徒劳的。
稍后 、当我们开始设计时
估算器或观测器 、这是相同的、
如果无法 观察到我们开始使用的系统、
同样,我们的努力 也是徒劳的。
我们无法从 无法观察到的系统估算 estat。
控制能力 和可观察性
是 我们稍后需要的重要属性。
现在、事实证明、稳定性 以及可控性
和可观察性、 所有这三项
如果 我们可以执行、就会有非常清晰的可视化效果
特定的近亲 DOF 变换
在系统上调用 da 模式分解。
我将向您解释 一下实际的模式分解
方法。
但是、如果您可以执行 eout、则会执行所有这些属性
您会非常清楚、 并且有好处
也是如此。
因此、我们将从 模态分解开始、
我将向您展示 所介绍的属性
以及 其他方面的术语。
然后 、我们将再次查看标准化的实现。
我向您展示了一 种、phas 可变规范形式。
事实证明、它 是另外两个被称为的位
可控制的规范形式 和可观察到的规范
因为此处是三角波形。
这就是为什么这个部分 恰好出现在那个部分之后
控制 能力和可观察性。
然后 是我要做的最后一件事
这 是一个 fairl yshort 部分、
最后要介绍的是冲头
下一个教程、我 将会或多或少地
每个教程都 将基于该教程。
它是一个双质量系统。
它由一 个有两个质量的机械系统组成
耦合在一起、
这样当你推动 水体时、其他质量就会移动。
但 两者之间存在某种能量交换
质量。
结果是振荡。
这是一个很好的、易于视觉化的系统。
它具有很多动态特性
让这些教程 变得有趣
这三种运动。
所以,我要启用系统。
驱动 ZVS 转换。
现在、我想先 解释一下这个概念
矩阵。
当矩阵使用 dfor 变换时、
您已经看到 、在 n 维度中、矩阵具有尺寸
n 乘以 n
矩阵为方形。
因此 、如果存在转换
在 三维空间中、从一个矢量到另一个矢量、
变换矩阵执行 三维变换。
例如、在这里 、我们有一个矢量 V、
它不由矩阵 T1运行
将矢量 t oa 变换为不同的矢量
V tilde。
因此、V tilde 是指向 不同方向的点 Gin
因为 它是由矩阵 T1进行操作的。
现在、T1、如 Wel las V 和 V tilde、
将以该坐标系的项 s表示
或者二者都是复数。
例如 x1、 y1和 z1、它们
可能是正交坐标
它代表矢量 和变换
权衡关系。
现在、让我们想象一下 、我们什么都不会改变、
但所有 这些信息都是坐标系
演示。
我们不使用 x1、y1、z1、而是使用 x2、y2、 Z2.
嗯,现在,相同的 tw omatrics-相同 的两个矢量
具有 slightl ydifferent 表示法。
因为它们的元件 将会不同。
因为它们 虽然指向相同的方向
从理论上讲、它们 在中重新呈现
不同的坐标系。
以及变压器 矩阵
从 V 移动到 V tilde、 这也会有所不同。
因为它的协调 帧发生了变化。
它在做的是相同 的事情、
但它是在 adifferent 坐标系中执行它的。
矩阵 T1和 T2 试用相似的矩阵。
它们可以实现 相同的变换、
但它们在 adifferent 坐标系中执行它。
它们与 所谓的旅游相关
相似性变换。
具体而言、T2 i 序列到 M、再到-1、
T1乘以 M、其中 M 是 相似性变换。
它将 Matri x 从一个坐标系变换
另一个坐标系。
且在 500 MHz 下,其 IP3 为 [听不清] dBm 时
不是吗?
您可以看到矩阵 M它必须进行测量。
它必须具有 与 T 相同的名称尺寸、
因为 T2的 esame 尺寸与 t1相同。
但是、当 你看到它时、M 乘以-1、
考虑相似性变换。
它将在 一秒内进入 com ein。
请注意,这是一个重要的属性,
那么、让我 花几分钟时间来讨论它、
难以仿真。
可以找到类似 的变换矩阵 M、它
采用 T1并使 T2对角线。
如果您可以 执行该操作、则会出现该情况
是 产生的许多好处
系统的电感。
该特定坐标系。
但 为了实现这一点、t1
必须具有一 组完整的特征。
否则、您可以 对 T2进行 tdiagonalize。
如果 T1没有一 组完整的特征向量、
您不能具有对角线 T2、
但您可以接近它。
出现的仿真形式、
称为 Jordan、用于 mrepresentation
稍后我会介绍。
但现在让我们想象一下,我们 已经不会有一整套特征的特征
这种 SoM 相似性变换可以实现
从而 使产生的 diagona lmatrix t2
该矩阵是对角线、bit 具有更进一步的属性
即您可以 对元素进行范围内的操作
对角线 Matri 的斜线、使其如此
以及系统的效率。
类似 的转变
这对你来说是一个 scolumns,它们本身就是这样
T1的特征向量。
这里有一些重要 的信息
一些特性。
如果 T1具有一 组完整的特征向量、
矢量 是定义的
CPU 独立
这些矢量 扫描用作列
以形成类似 的变换矩阵 M
因为 您知道、对于尺寸来说是可以的
你 有 n eigenvalue sin t1、t1是 n x n、
并且 您已经设置了完整值。
您有一个特征矢量。
每个特征都对 RHAS 中的元素感到羡慕。
因此、通过将这些列、 即 M、M 的列进行设置
尺寸也必须为 n b yn。
并通过使用 Matri x 实现相似性
变换、T2斜 线对角线、但不仅仅是
对角矩阵
T 1的特征值将是元素
对角线的对角线。
现在、在 我们了解该信息之前、
我 将向您介绍如何操作
您 可以使用状态方程进行状态变换。
现在、假设我 将一个状态方程式进行了打字
对于基于 关节状态选择的系统
影响。
我之前告诉过你 ,没有什么特别的
状态元素。
大家想用什么都可以。
那么、让我们假设 您做出一个选择、
它对 您来说并不是很有效、
您希望将它们更改为 不同的元素集。
没有理由不能这样做。
变化可能 会因所发生的事情而产生
称为状态变换。
那么、假设您使用的是 x 、并且您希望进行转换、
改用 v。 vis a different --
我是说它是一个状态矢量、但 我现在将其称为 v。
它与 x 通过 这个矩阵 M 相关、即
现在是 n 的任意矩阵
那么、我们要做的是将 这个直接置于状态
等式、x 点等于 x plu SV。因此、左侧不是
x 点不再出现、但它是 M 时间 SV 点。V 点是新状态
等于 AMV。
MV 只是插入之前 的 xwas,加上 v 乘以 u. v
不变。
现在、我们要做的是 、我的 SWE 将对两侧进行预乘法
与 M 的倒数相反、如果 您可以的话、现在这是一件好事
M 由特征向量组成。
因为 M 肯定 会反向。
因此、您可以 从 M 中找到反向
它是正方形的、因此尺寸 是我们所需要的。
爬虫 程序会以 M 的倒数进行预乘、
您得到 v 点等于 m t othe -1、乘以 M 次
五、看,类似 的状态转变
矢量。
加 n 到-1 乘以 v 乘以 u
我们执行 了相似性变换
在电压矢量上的优先权。
并猜测 负1 AM 矩阵的 MTO 值
变为负数的区域。
它就是带宽。
它 将在前导代码中具有该 eeenvalues
对角矩阵
我们要将其命名为 LPO。
让我们将 M t othe -1B、B1称为。
现在、这是状态向量 Rinto 转换状态。
我们现在需要集中讨论 输出方程。
可以执行相同的操作。
但它要简单得多。
因为我们不会 将 ETO M 反转。我们需要的一切
将 x 替换为 M 时间 SV。我们将其称为 C1。
因此、C Time M 将 变为 t obe c1加 v 乘以 UD
不受所有这些影响。
那么、现在我们有了 stat 公式和输出
该 新状态的 I nterms、v、
v 恰好是多少。
现在、独特的选择 -那么、这里有
无限选择。
您可以随意选择名称。
因此、我们不会将任何 特定状态绑定在一起。
您可以在 一个和另一个之间切换频率。
但对于这种声波 ,v 的元素
有一个特定的名称。
它们被称为 系统的表情。
典型系统运行 I nCharacteristic Set of Patterns、
梯形脉冲。
这些模式称为模式。
它是 状态矢量的电子元素的唯一选择
这些称为模式。
这之所以很 重要的原因是
您将看到 每个模式的时间
与所有其他模式完全解耦。
这种变换、 独特的变换
其中您使用了 eigenvector 列的 Mmatrix
转换为-使用 我的 neffect 矢量变换。
这称为调制 分解。
在以后您了解到 自己可能希望
第一个是 、事实上这些模式是不耦合的
彼此之间、可 提供非常清晰的可视化效果
放大数模转换器和输出之间的信号。
不仅是这样、而且通路 从状态中的输入端
到输出 的状态要清晰得多
如果 你刚刚采取随机状态、你会更好
矢量 MAPS
动态特性 更易于解决。
因为存在 标量、而不是矢量。
您可以对 随时间变化的运动进行非常简单的视图、
它使 系统的动态变得更加清晰。
因为通过公开这些 值、
您知道哪些是主要模式、
这一点不太重要。
请记住 复平面中的电子滤波模式、
复数中左侧的特征值
比 那些衰减得多
在右侧、它们接近 虚轴、
如果它是一 个持续计时系统、那么它们就会被执行
与我 FIT 的离散时间系统并联。
您还可以 获得更清晰的见解
介绍了 tw 属性
更早的可控 性和可观察性。
我 认为通路暴露在外的原因
实现平衡。
该过程在 一段连续的时间内类似
奈奎斯特路径。
只是曲折 的特征值是不同的。
那么,让我们来执行它。
我们将编写 模态相似性变换
我 现在将其称为 W、
因为它是一 个非常具体的转换矩阵。
M、但 我想将其称为 W
由 列 sof W 组成
独立 的特征向量的特征向量
矩阵 A。因此您不需要 对列进行调整、
每列都有 n 个元素。
这是一个 n x n 矩阵。
我将为 该矢量添加符号
因为经济转型也是如此具体
以及 称为模式的独特选择。
我将为 符号 q 进行 E过渡期、
元素 wil lbe Q1到 q sub n
有 系统的模式。
是的。
就是这样。
现在 、存在 r表示 法变化
我想让您知道。
这是 EMI 滤波器部分。
这里是 输出端。
因为这 是一个独特的选择
的列数
W、正如我说过的、我们最终得到 了一个令人激动的新系统
矩阵 DMS
这是一个交流电机。
Lambda 将沿其前对角线包含
A 的特征
那么、写入这些方程 、Iguest 这就是它们的外观。
扇 出的模式矩阵包含在其列中
A 的特征向量 和频谱矩阵、
因为它称为 Lambda 、所以我对角线矩阵在这里
特征值位于 主对角线上、
所有的 释放都是零。
模态矩 阵
是应用 于这两者的名称。
现在、模式输入矩阵是 W 到-1乘以 v
我们将把 W 插入 状态变换公式
那个方程。
我已经解释过的 λ。
现在、输入矩阵 、W 至-1
v。当您 进行此分解时、
将 该输入的各个行分开很有用
矩阵。
因此、我一直将这些行 称为 sbeta 1、beta 2
至 β n
这些是 WTO 的负1 v 行,即
为什么我这么写。
可以将其视为变量。
但实际上 、它们是行矢量、
现在、输入矩阵的第行中有 n 个。
输入 矩阵的 Beta 1和 beta n ar ethe 行、
W 至-1 V
因此、这会 影响您的状态方程
看起来像完整格式。
左侧的模型矢量的导数
等于频谱矩乘 以模态矢量、加
然后、这些是 新模式输入矩阵的行 s.
但我想它们是 一个矢量乘以输入矢量。
如果您愿意、它 将为我提供测试版
捕获所有 电子输入到特定模式的耦合。
然后、Lambda 我捕获 从 Qi 到 Qi 点的动态。
那么、您现在看到了我的意思、即完成 去耦。
如果您可以用 此表单编写 estat 公式。
那么、这是模 态输入矩阵。
这就是它在 到达单个模式时的外观
您得到的方程。
那么、现在请注意 、这个 Lambda 我出现在这里、这是
是完全标量。
关键点是 动态不耦合。
输入矩阵。
现在、模式响应、之前 的每个状态派生
可能涉及 所有其他状态。
因为 状态矩阵可能有一个 da 行
它 一直具有非零元素。
但现在你得到的是我 只需一个一阶
差分方程、 涉及相同的模式。
其他模式不 会产生任何效果。
这是模式的分辨率。
因此、它是用来 修复瞬态响应的特征值。
这将为您提供 模式演进的增长或衰减。
然后、参与 积分涉及 β I
这样我们就可以 得到响应的整形
是 确定该值的矢量
通过 与 B.的关系
输出矩阵 I sthe 乘积为 C 和 W
这对我的想法很有帮助
作为 单独的向量。
此外,可能会发生击穿,这可能
因为该 wil 向上乘以向量。
因此、伽马1至 GAMM an、单独的矢量、
每个矢量对 成个单独的-一种单模式
所有输出上。
那么、这就是我 应该看到的样子。
我是说它们是向量 、但考虑它们
现在至少是标量。
正如我所说的、每个伽马我 都会闪烁一个特定的模式
所有输出上。
以便输出矢量 等于所有这些乘积的总和。
因此伽马1乘以 Q1、plu sgamma 2乘以 Q2、依此类推。
现在、我认为这个图 将把它全部绑在一起。
因为这是我们 所做的所有图形。
我们已更改了显示方式
完全 独立的套件
状态、每个状态 都是完全的
去耦所有其他的。
现在为 729。
因为 Qi 取决于 y 点、反之亦然。
以及空间与所有输入之间的耦合
由相应行的低确定、
输入矩阵的输出。
以及所有输出之间的耦合
由模态输出矩阵的 I colum n 决定。
那么、您现在可以看到吗?
您已经获得了非常清晰的可视化效果
所有输入 如何影响一种模式、
以及 MOD 如何影响所有输出。
这 种表示非常明显
发生的情况。
现在一切都正常、 前提是您已经完成了
一整套 eigenvectors。
如果您没有 、那么您可以使用的单向方法是这样的
如果您使用 了树形特征值。
那么、在我向 您介绍如何操作之前
您使用这些 信息来描述
我 想要的属性 o fa 系统
简单地轻触一下 、如果您有问题、会出现什么问题
有一个去生成系统矩阵。
它只能通过 反复的特征值来实现。
即使这样、我 也可能不会发生。
你可能会幸运 、可以说、你已经成功了
才会出现退化。
但您仍然有 一组完整的特征矢量。
或者您可能运气不好 、丢失一个或多个
铜。
因此、系统会发生退化。
当您遇到 eigenvectors 时、您必须
如果您要执行 TA 模式分解、
您必须 替换 mby、替换缺失的
具有 被调用的矢量的矢量
广义特征向量。
这些 仍将是真正的特征矢量的正交。
但它们不会 满足矢量的要求
我 在前面展示的公式、它是什么
是负 λ i、乘以 WI。
我们寻求 了一种微不足道的解决方案。
因此、它们会对 特征去变体进行泛化。
您可以在网站上找到这些信息。
有一个很长的 yprocess 可以找到它们、
我不打算 在今天的研讨会中讨论这些内容。
但一旦找到 了它们、您就可以使用它们
实现平衡。
但频谱矩阵、对 角线 eigenvalues
不再 是真正的对角线。
它 将在斜升对角线中有一些元件、即1。
这意味着电 极二极管不会完美
去耦所有其他的。
将会有一个小的耦合 EBIT 开启。
Matxri 的形式 具有该对角线、
但某些受支持 的对角线等于1。
它们称为 Jordan 矩阵。
矩阵、即 生成的系统矩阵、
或频谱矩阵、其中 有 Jordan 块。
现在 、在时会出现可能的差分排列
您开始丢失矩阵。
但从根本上说 、特征检测器的编号是
实现的最大值
取决于您 的解决方案
获取公式 A minu si 乘以 λ i 再乘以 WI
α1α2 = 0。
这就是你发现了这些嫉妒者的方式,你还记得。
你这样做是为 lambda i 的选择
现在、我的 λ 一定 是可耻的、您可能会失去解决方案。
您可能没有完全 独立的解决方案。
您得到的数字取决于
在空空间维度 o fthis matrix 上、A 减 I 次
λ I.
空的 spac eDimension 会告诉您
您 将要获取多少个电子矢量
该特定的 Lambda I.
在本例中、 有一个整数
我叫 calin ghi、告诉你
可用 特征向量的数量
放大器驱动电路。
且 numrbe 介于1、
你将始终得到 1、而 Mi
特定 特征值的多重性。
如果您幸运、您可以使用 GE TA 全套、在这种情况下
你已经得到 了完全不一般的东西。
我们无需担心。
但是 、如果您没有这么做、
嗯、如果 你只有一个、你
需要这些通用 的去 igenvalues、
最后得到完整 的 Jordan 表格展示。
如果 您具有介于1和多重性之间的
你最终 会看到 Jordan Blocks 出现。
频谱矩阵 x 中有特定的块
它们具有1的超级对角线。
但它们并非全部为1。
它们中有些被压入。
让我来向您展示 一个有关这方面的快速示例。
这可能是一 个 Jorda 挡块
与特定的值相关联
具有一定的多样性。
同谋 是数字
对角线上的元件数。
您可以看到 、所有元素都是0、
但这几个除外。
这称为 Jorda nblock 或 Jordan 矩阵。
因为这是唯一的矩阵。
例如 、这里是一个五阶系统、
它具有三个特征值。
这有两个主要目的。
我有两个在-2处 、两个在+ 3处。
这 是一个不稳定的系统、1位于-1。
那么、在这个 scase 中、会出现什么
是 针对负2处的 tw oeigenvalues、
有一个约旦集团 的 kof A。你看到了吗?
它位于对角线上、 因此特征值
XY 尺寸更小。
但我们 需要的广义的 eigenvecto 在那里放置了1。
然后 、对于3、还有相同的细 gg
一个 Jordan Block 出现 在 ghere、对角线上有3秒、
对角线中为1。
然后是单 个特征值
给了我们一个 与它相关联的嫉妒。
因此 、您会在右下角得到一个很好的-1 i
类似情况。
现在、我将执行 一个快速教程、
只是为了向您展示 如何使用模式分解。
一次、它不再是 这些降压转换器的基础。
当 我清除其他一切时、请与我保持联系。
在本例中、我们在教程6.1中
分解-- 我不知道我做了什么。
为此我 道歉、我按下了一些东西
我不应该把 它分解
组成模式。
那么、很显然、这是 一个三阶系统。
我不知道它 将是怎样表现的。
但它显然有两个输入。
因为输入 Matri x 中有两列。
因此、我们有三个状态、 我们有两个输入、
我们有单 输出、因为
输出矩阵 C 的形式。它有一行。
因此必须有一个输出。
它具有 thre ecolumns、因为我们
知道有三种状态。
输入矩阵为0 - 转换矩阵
很抱歉、是0。
它包含两个元素。
因为有两个输入。
它有一行、 因为有一个输出。
那么、让我们分解 成它的组成模式、
看看会发生什么情况。
那么、首先、我们 要做的就是 hthen
使用 与我相同的方法构建系统
之前在 MATLAB 中展示的。
在我们进行 模分解之前、
我将绘制其响应。
我们将看到其 响应变化
模式分解后。
首先、我 将要构建
阶跃响应 、并绘制三种模式。
现在问题是 、这里有两个输入。
那么、阶跃响应 、问题是-原因
它 有两个 Pste 输入。
因为当 您执行一个步骤时、MATLAB 会对 LDO 产生什么影响
具有两个输入的系统上的响应是
有两组结果。
一个是 施加到第一个输入的 ste、
而第二个保持为0。
另一组结果 、当第一组结果保持为0时、
第二个应用 了阶跃输入。
因此 、这里将会有状态图的 tw oset。
它将反映 状态的维度
由此产生的矢量、 状态矢量结果。
我们可以开始了。
仿真结果如下。
上图是 三种内部状态的演变
当我们有阶跃应用 程序 dto U1、U2保持为0时。
然后 、在这里的底部图中、反向是
这些是 随时间推移的状态解决方案
因为 U1保持恒定、 而 nu2施加了阶跃。
现在、我们要做的是 perfor ma 模式分解。
我们就是通过这种方法来连接它的。
此 CLC 只清除 工作区中的任何内容。
这使事情 对我们来说有点整洁。
然后、我 将再次执行 EIG 指令。
请记住、这是 从中提取的特征值。
但当您使用 这两者的结构时
电 容、电容和电容参数
将返回模态矩阵 W、
频谱矩阵 λ。
嗯 、键盘对 lambda 没有注意。
那么、我将使用大写的 L
这是两个矩阵 、n x n、3 x 3
在这种情况下、将返回这些值。
您为其提供系统 mmatrix a、而不是仅提供平衡
意味着不要平衡 特征检测器、
我的意思是,我只是把 电子贸易机会这样做。
没有关系。
现在 、你已经把 W 变为原来的值。你可以
在类似 的变换中使用它
提取模式输入 和模式输出矩阵。
请记住、模式输入 Matri xwas W 到-1乘以 B
因此、我们将反转 W、 并将其乘以 B
我是雅斯特- 嗯、
我将断开它。
因为我很感兴趣、所以我 将行视为向量。
稍后您会看到。
然后、模态 outpu tmatrix 为 C 乘以 W
然后 、OIS 将代表它们
作为电流 LSB。
我们来操作一下。
您将看到 A、B、C 和 D 消失、
我们最终获得 L 和 MIM 0和 D
我不知道为什么 w EDID 不会结束-好的。
好的。
因此、它所做的就是再次为 我提供 A、B、C 和 D。
但这点我 是作为频谱矩阵的点。
这是 以指数值的 gof 表示的 λ
实现平衡。
这就是 EN/UVLO 引脚。
很好。
我想知道为什么它会被转置。
这实际上是正确的形式。
我不得不思考 为什么它被转置了。
但这是 输入矩阵的巨大形式。
因为它有两列。
有两种方法。
然后,还有交流损耗。
因为 其中有三种状态。
然后是 outpu tmatrix、模态输出矩阵、
透射 性 nmatrix 仍然为0。
我们现在将 执行相同的操作
我们在 Carrie dout 模态分解之前做过。
我们将进行预设 、并绘制状态。
现在,这是问题所在。
对于这种特定的状态选择、
因为我们有一 个完整的对角化光谱矩阵、
我们现在必须具有完全去耦内部状态。
每个状态 都取决于其自身的状态。
因此、我们得到了等于 λ i 乘以 Qi 的 Qi。
它们耦合在一起。
它是第一 个 orde rdifferential 等式。
这里没有其他东西。
您从过去就知道 、一阶解决方案
差分均衡 呈指数级。
因此、当我们计算 并解决这些问题时
对于阶跃输入、我们应该找到 1减去指数衰减
代码。
我们得到的确实是这样。
那么、这些是状态 、以及它们现在是如何演变的
变化情况。
因为它们 彼此去耦。
您可能会看一下 并思考、嗯、好的。
他告诉我们。
那么、什么。
可能系统也发生了变化。
但我 的观点是、它只是这样
系统实际动态的状态变换
不变。
换言之、 整个系统
无论 我是否表示、行为都完全令人感到羞耻
使用 SoM 耳本选择的状态、
或这个特定的选择。
我将向您展示这一点。
现在,我要 做的是,我要
绘制原始系统。
Y1的图、这是 原始系统的输出。
第二个传感器已经成功连接。
好的、这 没什么特别有趣的。
这就是系统的行为方式。
现在、我在 这里的 GTO 中所做的是、
这是一回事。
我将绘制 该图 Y2的顶部、Y2
是发射 分解的输出。
我 希望、所有这些变化
是该图的颜色。
它应该从蓝色变为绿色、 因为它是同一个系统。
它只是国际 动力学
以不同的状态选择表示。
这就是调制 分解为我们所做的事情。
[INAUDIBLE]?
使用 GA 模式分解的主要原因
从 mthe 输入到输出的路径
更清晰。
该属性意味着 可控性的属性
和可观察性、 可预测性等
更容易实现可视化。
看到 GPIO。
没错,这是问题的关键。
因为它会引导我 了解接下来将要做的事情。
[INAUDIBLE]?
是的、这是可能的。
[INAUDIBLE]?
嗯、它会使 引脚感到它
可能会将注意力集中 在非主导模式。
因此、它可能在这方面有所帮助。
或者您是否希望 简化系统
通过减少它的 orde rof、它可能会对您有所帮助
做出该选择。
因此、我 需要在控制设计方面提供帮助的原因有很多。
[INAUDIBLE]?
是的,确实如此。
[INAUDIBLE]?
嗯、有点像。
对,很接近了。
但我想摆脱 超前和滞后的想法
补偿器、也 是根轨迹的除法器。
因为在 系统中-我昨天介绍过
其中我们使用 doutput 反馈、我们
必须 关闭闭环
特定线路上的极点称为 loci 的复平面。
我们 可以更改的唯一精简 gg
是增益、沿 这些轨迹移动轨迹。
状态反馈控制的一大优势
您可以在 复平面中任意选择您喜欢的任意值
放置极点。
您具有极大的灵活性
接近 的环形极点所在的位置。
您 正在使用的栅极、FAC
而 不仅仅是输出中的状态矢量
好处。
因此、我认为这有助于 推进这一决策过程
极点的选择。
现在、我 将稍后更多地使用该小数位。
但我想 在一段时间内继续保持 kabout 稳定性。
那么,有两种 类型的函数。
在 我们继续之前、我想告诉您、
并了解如何使用它们。
第一个问题是,我们 可能会立即这样做
视为稳定的系统。
这一制度占有 财产
称为渐近 cti 稳定性
这意味着它的状态 i nthe initial condition
随着 时间的无限变化、
将收敛于该 电子平衡点。
因此、这相当于一 个稳定节点或一个稳定焦点
在我 之前向您展示的相位纵向中。
因为这种状态 会跟随某种路径。
这是一个稳定的焦点、 最终会随着时间的推移而出现
它稳定地稳定 在平衡点。
它称为渐近稳定性。
对于什么、有一个字的 ydefinition
这意味着、就 可以在多大程度上取代初始条件而言、
它与 平衡点收敛的事实。
因此、具有 连续时间值的系统
小于0、或者 如果是 rdiscrete time eigenvalue
小于 1的模数、具有属性
渐近稳定性。
现在、在 本幻灯片中、我能不能
做一些看起来 很明显的事情
您很清楚、 这一点非常明显。
因为它稍后很重要。
在稳定状态下 、对于渐近稳定系统、
如果是连续时间、您 知道稳态是
由 T 等于0的 x 点定义。
这意味着 estat 不再改变。
它达到 了它的固件点。
那么这是稳态。
但请注意、如果它是 离散时间系统、
存在陷阱。
因为我 在稳定状态下的意思
是 nex tstate 没有不同
输入和现态。
状态 XK 加 1与 XK 相同。
因此、当你保持 稳定状态时
对于分立式系统 、重要的是
右侧 不再是0。
这将在 我们看设计时再次出现
控制 系统中的稳态的高电压基准。
但我想提醒 您注意这一点
一个重要的差异。
实际上 、这是唯一的一个
稳定部队的差异
时间和 离散时间系统之间的差异。
因此 、稳态定义存在差异。
但无论如何、我认为您 可能[听不清]
想象一下,“那是一 种很棒的稳定。
现在 存在某种稳定性、
它位于 phas 纵向图中
其中平衡 点被称为中心。
一般而言、我 称为 Lyapunov 稳定性。
Lyapuno v컈 뚨 所说的是
如果您将初始 状态从其平衡状态中移位
然后让它运行、 前提是您没有
让它从 该状态转得太远、
它将对 状态进行收敛、
也可能不会达到无穷大。
它可能会保持 在平衡的每一个特征中
不 会在比赛中到达它。
这是 一个系统示例
它具有复杂的共轭 值、如果它是连续的
时间、或单 个转盘上的电子值、如果它是离散时间。
因为这些振荡 是持续的。
它位于边界上、不稳定。
它称为预翘曲。
有时您会看到具有 Lyapunov 稳定性的系统、
被称为稳定的是 Lin 的 Lyapunov 感。
这不是我们担心 的事情。
但术语会不时出现 、尤其是
非 线性系统的应用。
但执行 此操作的系统、在本例中
它是二阶 的、它的相位纵向会是
属于 中心的类别、
它具有利亚普诺夫稳定性。
现在 、绘制了两个车床图
就输出而言, DPWM 模块 2 和
此电路的频率响应。
我将讨论的是、没有 WIS 如何涉及输入。
因为 输入的有效性允许
我们将在 内部和外部进行区分
稳定性
首先、 内部稳定性是
耦合的属性介于 输入和状态之间。
它有时称为边界 性状态稳定性、
或 BIBS 稳定性。
有时、它是回调 式内部稳定性。
因为我们在谈论内部 变量集
称为状态。
提供 RA 有界输入、
状态保持 受限
获得 BIBS 或内部稳定性。
如果您解决 稳定性的均衡问题
主动能量传输。
显然、您正在寻找 外部信号。
以及 外部稳定性
当有界输入仅 产生有界输出时定义。
您具有 BIBO 稳定性。
现在、因为输出均衡 仅是代数方程
涉及到状态、则会提供 有界输入
有界状态稳定性、您会 自动获得有界输入
宽输出稳定性
因为在 该状态下、动态特性仅在那里
但不会相反。
这并不一定是一 个关键问题、因为系统是这样的
外部稳定、 内部稳定。
要确定该值、 您需要确定
状态如何从 内部耦合到输出、
主动能量传输。
您可能具有内部状态、这些状态
会像疯狂的那样振荡、但 不会耦合振荡
到输出 电流、因为存在
是输出矩阵中的0个元素。
因此、内部 稳定性是肯定的
可保证外部稳定性 、但不会相反。
好的,
现在、让我们来了解 一下可控性
10K 欧姆的电阻器。
稳定性概念也 会进入这种情况。
我有她 的 eis 四阶
已 执行模式解调后的系统。
它与 我之前展示的图表类似。
因为每个 表情都是完全的
与所有其他组件不耦合。
输入和 每种模式之间的耦合
由 W 减1 B 矩阵的 sw 行确定、
以及从 EAC 模式到所有输出的耦合
C Wmatrix 的列、这些伽马元素。
现在、 这是 W 的异或响应行
负1 B、因此 Bi 转换器 是非零值和伽马 I
非零、很显然 、tmode 是通过耦合的。
因此、您可以说是 因为输入
耦合到该模式、 我可以影响该模式
来减少输入电压。
因此、我 所说的模式是可控的。
因为 CW 矩阵的相应 gcolumn
非零、当该 模式移动时、它是
某种程度上会影响 至少一个输出。
因此、这 种模式的情绪
观察到的相关事物。
模式1被认为是 可控制和可观察的。
您可以看到我 在这个图上进行了详细的了解。
因为您知道该 异或响应矢量、
Beta 1和 γ 1为非零。
现在想象 一下伽马2为零的位置。
这意味着该模式不 会耦合到输出。
我们无法 通过观察输出来确定 gSimply
Q2是否稳定 EOR 为不稳定模式。
因此 无法观察到 tmode。
但由于 β 2是非零、 因此它与输入耦合。
因此我们可以对它施加影响。
这 是一种可控但无法观察的模式。
当 reverse 为 true 时、您可以
看看 模式3会发生什么情况、β 3是零、
但伽马3不为零。
因此、这种模式是不可控制的、 但至少可以观察到。
最后、有一种模式 、它与任何东西都是解耦的。
它是一 种无法控制的模式和一种无法观察的模式。
因此、这些属性 非常明确、
模式分解后、它将立即开始运行。
首先、 正如我说过的、它们的重要性是、
您无法确定 任何相关内容
内部可控性从 传输中循环伺服
功能描述
这些只是 状态空间描述中的属性。
幸运的是、物理 系统
控制 器和可观察的、
这意味着、当您 从头开始构建 astate 空间模型时、
某种系统、 即实际系统本身
那么这里的电压将大于 VOH。
但您的模型通常 包含一些简化
或一些假设、意味 着模型可能不会
具有这些属性。
因此您无法 控制
系统或观测器的型号
您的系统模型。
如果您选择的 stat edoes 具有这些属性、
然后执行 astate 变换
不会更改属性。
因此 、您使用的 wha tstate 选择无关紧要、
证明其正确性。
和可观察性 是系统独有的、
而不是选择状态。
你往往有各种原因使稳定部队有问题。
最常见的原因是您 忘记了有极点
在 您的转账职能部门、您可以在此处取消或取消预订
或 等效的传递函数
说明中有 偏斜极点和零点。
但由于 其他原因、您可能会运行 int oit、
例如、对状态进行明智的选择、
或可能是国家数量。
这些东西也可能会降低 可控性
简称 WCT。
首先是包络。
总结 一下左侧的两张幻灯片 sago
IAR。
因为只是很喜欢 动态、
从 输入到模式的连接路径、
β 1和 β 2列矩阵矢量
为 SPI。
Q1和 Q2 与输入进行爬电耦合。
那么,这是一个 RAM 地址。
而系统在黄昏中是无法控制的
功能模式。
但它是具体的模式 2、这是不可控制的。
因为模式2未 连接到输入端。
Beta 2是一个0矢量。
这是 IC。
因为这个 特定的特征值
位于右半平面。
这意味着 系统不稳定、
无论如何、GWE 都无法做到这一点。
因为我们无法 控制不稳定模式的通量。
这种薄 的 gg 可能不是很明显
如果您只需要随机 选择状态变量、
以及完整的可变状态 器描述。
但 它可以避免雪的存在
系统中存在不稳定和不可控的仿真二极管。
这将在稍后引发问题。
因此,如果您 在这里有电阻,
分类是 可控和不可控的
非常清楚。
您只需查看 rnonzero beta i 矢量。
这 是一种查看事物的方法。
还有 一个代数测试
适用于一般情况。
代尔拜 ctest 就是这样的。
您首先必须构建 可控制性矩阵
从现在开始、我将调用 P可控性矩阵
这样。
现在、这是 calle da 分区矩阵。
我想这是 昨天的 Matri x代 数笔记中的内容。
一个分区 Matri xcontains 元素
它们本身就是矩阵。
eis 上的这个特定结构如下所示。
它是 B、A 乘以 B、A 平方 B、一直到 A 到 n
减1乘以 B。让我们细小 它的尺寸。
B、您知道、i n x r matrix。
它有 n 行和 r 列。
a 是方形矩阵。
因此它不会 改变行数
有很多类型。
AB 将 会进行仿真、因此是 n x r 矩阵。
A 平方 B、类似地、n 除以 r
因此每个 分区都是 n 乘以 r
因此 、整个东西中都有 n 列。
您有 n 行、您 有 n 次 r 列
一个示例。
然后、你所做的 是、你看一下它的排名。
现在、请记住 矩阵的侧面
是 最大非零决定因素的尺寸
任何位置。
那么 、对于这个矩阵、你可以得到的最重要的排名是什么?
你不能大于 n
因为它中有 n 行。
它有 n 乘以 r 列。
那么、您有一个输入。
它将 是 bEAN n x n matrix。
这就是 EMC 问题。
如果您有10个输入、它 将是10n 的10倍。
但它不能得到大于 n 的 bigge、因为你
需要一个方形 Matri xto 具有一个决定因素。
因此、你 可以拥有的最大的 RAN 是 n
现在、如果这个特定 矩阵具有秩 n、
系统是可控的。
您是怎么做的。
对于离散时间系统 也可以这样做,
唯一的区别是 电位变化、A 的 C、
B 的伽马。 否则、您将构建
控制 器矩阵、并对其进行评估
完全相同的方式。
您 可以说有 SoM 的表达方式。
如果您只有一个级别 o fv、其中 v 小于 n
然后您知道您 只能使用 v 可控模式。
您有 n minu SV 不可控模式。
因为其中 n 减 v Beta 检测器为零。
还有一些人在可 控制性指数中进行了定义
因为 它是必须具有的最小数量的分区
添加、直到您获得全排名。
嗯、无论如何、这是第三 个可控制性指数。
现在、可观察性非常 相似、令人惊讶的是、
令人震惊的相似之处。
我有一个问题。
请说。
[INAUDIBLE]?
是的。
[INAUDIBLE]?
当然。
[INAUDIBLE]?
好的。
[INAUDIBLE]?
你会说 滴滴不会改变。
它 将永远到达一零。
你们得到的是这个吗?
是的。
就是这个[听不清]。
它将如何激发?
是的。
答案 是、我在数学上讲这个东西
将永远保持为零。
实际上,我们没有这样做过。
存在影响 系统的噪声和扰动
实际上、您只是 不知道。
它不会保持为零。
但你已经确定了你 不能影响它的 FAC
低电压。
因此、无论发生什么 情况、您都无法更改。
什么都不会改变。
因为会 有激发它的 SoM e扰动。
然后实习 YIT 将会增长。
但从数学角度讲、您是对的。
没有什么可以激发它的。
因此、理论上、它 永远不会保持为零。
但这不是必需的。
是的。
这是 ROM。
音频正常吗?
是的。
好的。
因此、继续 观察、
没什么特别的。
我们解决 了可观察性的均衡问题
放大数模转换器和输出之间的信号。
它是 CW 矩阵的列 s
它为我们提供该信息。
如果它们都是非零、 那么-即使是模式
通过输出耦合。
因为 γ 1、即 refxample、决定了
Q1与 所有输出耦合的方式。
在左侧、有 一个可观察的系统。
它仍然是一个不稳定的系统。
因为如果 N 大于 0,
它是一种 弱实时系统。
大家可以看到这一点。
因此、该电子模块 将会振荡。
但至少我们可以检测 输出端的振荡。
这是 可观察性的定义。
右侧是 I hav EAN 不稳定系统。
我认为它具有相同的模式 、因此具有相同的特征值。
但这是不可观察的、 因为伽马2是0。
CW 矩阵的第二列为0、
因此、secon dmode 未连接
任何输出。
我们 没有什么可以检测到什么
第二种模式将会执行。
这 也有一个代尔拜克特尔。
它涉及形成 顶点矩阵
时间反转函数。从现在起、P
Q 将为 这两个矩阵保留 dd。
因为我们现在非常需要 GTO。
现在形成 了分区
从 C 转置、转置、 转置、转置
转置等。
您在 该矩阵中查找运行 kof n。
如果您有它、 则可以观察到 nthe 系统。
如果您没有 该系统、则无法观察到系统。
离散时间有一个并行
替换为 C 的系统
现在有两 个相关的附加属性。
其中第一个是 我的扇贝稳定性。
IO_SUP 与 RX_SUP 相同。
但问题是仅针对 不稳定模式。
我来举一个例子。
这是一个系统、它是 一个无法控制的系统。
因为我们知道 FIRS tmode 与输入不耦合。
因为 Beta 1为0。
因此、这个 modeCAN 执行它所需要的任何操作。
w eCAN 无法影响这个模式。
但它是一种稳定模式、 至少它是稳定的。
但是、第二种模式是不稳定的。
但它具有一 个非 Zer obeta 2矢量。
因此、它通过 输入耦合、
因此、w eCAN 会影响它。
我们可以稳定 输入的 b y 操作。
因此、我 可以控制该系统、
需要的电压电平。
但至少它是可以稳定的。
但可以设计它。
还有另一 个与此相同的 mter。
但它会应用于输出。
它称为预翘曲。
它是可观察的、但只能寻址 到不稳定的模式。
实际上、它是 Sam esystem、
但在这里、您已经获取 tgamma 1非零值、
第一种模式是耦 合到输出。
第二个问题是可靠性。
现在、这里的第一 种模式是不稳定的。
因此、它 是一个可检测的系统、
降压-升压解决方案的大门。
第二项要求源于
虽然它不可观察、 因为它是稳定的
则可以说器件具有 ELDRS。
这意味着、如果 涉及到一个 yinternal 振荡、
系统内部任何不稳定的东西、
至少您可以检测到它。
因此、我通过 两种方式定义了可控性和可观察性。
我已经定义了稳定性 和可检测性
是可控 性和可观察性
但仅解决 不稳定模式的问题。
下面我们快速测验一下。
因为这 真的很有趣。
我们将对 结构特性进行调查
四阶系统的性能。
我 没有任何 IDE。
因为我不记得 本教程是如何实现的。
那么,让我们看看两种情形。
首先 、我们创建系统。
这里没有 什么令人惊讶的东西、
仅使用 SS 和 A、B、C、 D首先、我们要介绍
进行稳定性分析。
现在 、MATLAB 中有一个手录。
您不必担心 像 eigenvectors 这样的事情
和特征值、以及在 左半部分计划中的工作情况、
或右半平面。
您只需键入即可保持稳定。
是稳定的、它真的需要所有的东西 、不是吗?
因此、 您所做的是、您键入的是稳定的、
或者它是稳定还是不稳定。
是的。显然这 是一个不稳定的系统。
我们还不知道它。
但它是一种电路外的 EOS。
现在、我们要在 GTO 中做的下一件事是检查可控性。
我首先要做 的是我正在看
显示了片上 SRAM 的大小。
这将告诉你维特 尼-现在如果你在这里键入1、
它将告诉您 行数。
如果您键入2、则 会显示列数。
因为 它们的尺寸为1、2。
但我知道 AIS 是一个方形矩阵。
因此、这并不重要。
这将告诉我 系统的尺寸是多少。
当然、在 本例中、它是4。
然后、在这里、我 介绍了重要的一行、
因为这是 可控制性矩阵的构造。
CTRB 构造 控制性矩阵
您 所需的两个抹香
为其提供 系统矩阵 A、
和输入矩阵 C
因此,我们 现在对 P 退了
我只需要了解 P 的级别
与 A 的尺寸相同、它
是系统的等级 和系统的尺寸。
如果是、 则系统是可控的。
如果不 是、则是无法控制的。
很高兴这 是一个可控制系统。
因此 、在那里的某个地方有一个不稳定的仿真二极管。
但至少它是可控的。
因此、您可以说 该系统是可稳定的、
尽管它不稳定。
现在、我们将为 可观察性做类似的事情。
我将使用构建 可观察性矩阵 Q
为其提供 A 和 C 矩阵、
然后再次检查排名。
希望运行 的 kwill 等于4。
不幸的是、它不是。
等级小于4。
因此 、系统无法观察到。
并尝试 去探索神秘之地
在这个系统的后面、我们 将进行模式分解
你会发现这是为什么。
那么、我们将 共同定义 A 的 EIG
为我们提供一 个模态 d光谱 矩阵、
然后计算调制 线性输出和输出矩阵。
这是下一个脚本中的目标。
我们可以开始了。
现在、在我们 进一步讨论这个问题之前、
一些属性 现在变得清晰。
因为我们所做的都不 是模态分解。
我们显然拥有 完整的一组特征值、
和完整的特征 矢量。
由于所有 这些值都不同、
因此,我们知道我们 不会成为一整套特征的特征。
但是、如果您看 一下它们、左半平面、
左半平面 、你得到的是加1。
这就是 系统不稳定的原因。
这里有一种积极的价值。
3号为正。
嗯、我们知道它是 一个可控系统、
所以 我们不应该感到惊讶
einput 矩阵的所有行都不为零。
但我们也知道我 无法观察到、
这意味着 模式的 SoM eof 不是
噪声有多少。
输出 矩阵的头两列
为0。
因此伽马1和 伽马2都是0。
但伽马3和 伽马4不是0。
我们已准备好 [?
我们有 ISO-21848。
我们有 ISO-21848。
现在、 我告诉过您的其他一些属性
稳定性 和可检测性。
那么、让我们 先处理稳定性问题。
这 是不可扩展的系统吗?
是的。
米歇尔说是的。
每个人都能实现 经济转型的稳定?
它是稳定的、 因为所有模式都是如此
RTI = 参考了输入
因此 、无论模式的音调如何都是不稳定的。
它通过耦合。
因此它 可以稳定下来。
这是可检测系统吗?
为什么没有呢?
好。
嗯,请思考一下。
可检测性是可观察性、 但仅解决此问题
ECG 波形总是延迟。
因此、我们不是处于 稳定模式的中间位置
不稳定的情况。
嗯、它是第三个 不稳定的模块。
因此、我们将提高 可检测性、
可观察性。
我们需要 CW 矩阵非零的第三个色谱。
就是这里。
通过观察 gthe 输出、我们得到了
至少得到 了这个东西的电子信息
变为负数的区域。
这 是一个稳定的电子和一个可检测的系统。
但这并不理想。
这是无法观察到的 、整体来看。
因此 、该系统具有这些属性。
好。
我希望我们几乎就在那里。
我们有两种形式。
我不打算对这个进行人工操作。
因为我已经完成了。
这几乎是午餐时间。
这是 phas 可规避的规范形式。
这两者之间的任何不同之处
我 在上一张幻灯片中展示了相位
变量规范对于 mon、它是标题。
它称为控制 器 ecanonical 表单。
您可以通过 我向您展示的过程来实现这一点
开始,
您会得到矩阵的非常识别的电子结构。
您可以从 系统矩阵中获取该值
其中所有 的不祥因子系数
显示在底部行中。
除 超对角线外、矩阵的其余部分为0、
即1。
这是因为状态的选择、 即状态选择
是相位。
B 矩阵、输入矩阵 、为0、除了最后一个矩阵。
C 矩阵、 输出矩阵、
包含 分子的系数。
当您看到它时 、您就知道您是
处理控制 器 ecanonical 表单。
它称为自动生成该表单
可控
今天 下午、我们将使用这种形式
设计状态空间系统。
现在 、有一个类似的形式、称为
可观察的规范形式。
我将 很快地向您介绍、
告诉你 滴滴的关系非常密切
与可控 性表单非常接近。
该矩阵是 可观察到的规范形式、
现在我将调用 OCF。
好。
您有 CCF 和 OCF、 您可以看到这些缩写。
OCF 系统矩阵 与 CCF 系统矩阵相关
锁存器。
这就是所有的不同之处。
现在来看看关断,
对于观测 表例形式、
输出为 经济过渡期
控制 器规范形式的矩阵、
这两者也与 转置相关。
在某种意义上、可 控制的输出矩阵
是 可观察输入矩阵的转置、
反之亦然。
接下来,请看这里的
观测 表例形式的矩阵、
它与输入矩阵相同
可控制的 canonica lform、只是转置。
因此、如果您了解 一下音调描述、
您已经自动 获得了另一个、
如果您现在有 转置、OCF 和 CCF。
现在、 当我们来到这里时、这些东西令人非常愉快
进行状态空间设计。
CCF 更改了状态 反馈的设计
非常简单。
和 OCF 表格让 观察员设计人员
简单的提示。
现在它们是 calle dcomp配套 表单。
它们通过 这些转置相互关联、
我在 上一张幻灯片中向您介绍的内容。
但是、这种关系我 非常强大、
您最初可能想象的更强大的功能。
这种关系的名称 称为 duality、
这意味着这两个系统 被这些矩阵所描述
相反的信号线。
因此、您可以选择 其中一个的可控性
检测 对方的可观察性、反之亦然。
因为如果您在寻找 P 和 Q 矩阵、
它们的关联 方式与我的关联方式不完全相同。
请记住、P 矩阵是 B 分区 B、A 乘以 B、
乘以 B
可观察性矩阵 I twas C 转置在 B 位置、
和 A 的转置 I nplace。否则
完全相同。
因此、当您检查 其中一个的可控性时、
您实际上正在检查 另一个是否具有可循环性。
这种类似的并行功能有助于我们以后的工作
详述这一点。
因为使用 的技术是这样的
电压反馈控制器的设计
与 您用于观测器设计的完全相同。
这是一件充满力量的事情。
因为您只 能获得一组流程、
您可以执行这两个作业。
在这一部分的最后,
我 将向您展示一个非常简短的教程
可能会出现什么问题。
有一个术语"最低 限度实现"
这意味着您找到 了具有最小空间矢量的空间矢量
可能的尺寸。
以及您的模型可以使用的 GIS 的功能
在那里有状态、什么 都不做。
保存的操作太多。
您可能有 第三阶系统。
但你不小心 给了它四个状态。
当你这样做的时候 ,事情可能会出错。
通常 会出现问题的是您
失去 了我刚才讨论过的一个属性。
例如、您会丢失 可控制性属性、
这意味着 UCA 无法控制系统。
因此、您必须开始 确保已经完成了
具有可控性。
如果没有、请看一下。
您是否在处理 实现问题?
为了说明这一点、 我将执行它
以组织形式提供、教程6.3。
这意味着、对 可控性和进行调查
三 阶的可观察性属性似乎无害
一个输入。
因为 B 矩阵是 acolumn 矩阵、并且有一个输出、
因为 C Matri 坐标轴是行矩阵。
那么、让我们在 MATLAB 中查看这一点、看看会发生什么情况。
因此 、从一开始就没有什么令人惊讶的、
我们将开始 建立这一制度。
命令窗口中没有任何显示。
但这些是 工作区中的 Matrice swover。
我们已经构建了系统。
现在、我们将确定 首先可控性、
使用过去 用过的技术,
构建 可控制性矩阵、
并确定其等级是否为
等于 系统矩阵的大小。
如果是、 则系统是可控的。
如果它不 是-嗯、它是不可控制的。
但令人高兴的是、这是一个。
因为系统 mmatrix 是3 x 3。
这是 P 矩阵。
我们正在寻找它 中的大非零决定因素。
实际上、它会发生 这种情况
具有非零决定因素。
因此 、该矩阵的排名为3、3等于3。
因此、这 是一个可控系统。
现在、让我们继续、为 可观察性做些令人遗憾的事情。
我们已经知道 n 是3。
我们不必重新计算它。
可观察性、这 是可观察性矩阵。
不幸的是、最大 非零决定因素是2
降低了 2 毫瓦。
在这里、它具有2级。
2小于3、这 是一个无法观察到的系统。
现在、为了找出 原因、我接下来要做的是什么
查看 传递函数的 stat
部分。
因此、我将 使用脚本转换 S STO TS
要转换为 transfe 函数描述、
然后 TS 从 它构造 G、即 etransfer 函数。
我们来看看这个。
简单地说、好的、 到目前为止没有什么明显的。
它是一个三阶系统 、其中包含两个零。
现在、我们接下来要做的是、I SWE 将使用此 ZTK 脚本。
请记住、这是 一个显示极点和零点的函数
信息作为数组。
因此、这将告诉我们 分子是什么
分母是相同的。
这将显示 极点和零点。
此时、您 可以看到存在问题。
因为 这里有一个阻抗极点。
一个极点位于 S 等于 sminus 1、另一个零点
时间极点开始。
据说这 是一种微不足道的认识。
现在、我在这里看到 一个 TA 相当简单的系统。
系统会变得更 复杂、
订单数量众多。
找到这些东西有点难。
有时您不需要 转至传递函数
以查找它们。
但很高兴 MATLAB 为您提供 了一个名为 minreal 的脚本。
看到、 MATLAB 花费多少钱-花费多少钱是惊人的
MATLAB 工作将从它中取出。
MinReal、您将为我提供 传递函数。
在本例中、G1是 ZTK 形式、然后是
将返回 rtransfer 函数、
控制器,即这里的 EC。
在本例中、它将为 我们移除该消除极点。
现在、我们有 一个二阶的 transfe 函数。
我可以继续 对状态空间进行疏浚
评估它的稳态响应。
现在、我 在做它的方式、你会的
这也是一件事 、就是回来
这些系数数组进行比较
该设计的链接。
这与该 TS 数据不相关。
它返回枚 举符和分母的数组、
将系数转换为数组。
然后使用 TF 到 F STO 返回另一个方向。
将函数 转移到状态空间、
它将这两个数组作为 对四个矩阵的返回值
空间描述中所需的所有信息。
我们可以开始了。
现在有 了秒序系统
以国家空间形式表示、 这是一种最小的实现方式。
最后一件 行李简单地确认了
我们现在处理 的是可控和可观察的
转换器。
它与 之前应用的测试 SWE 相同、
构建可控 性和可观察性矩阵、
并在 本例中检查它们的侧面是否为2。
因为 系统的顺序减少了1。
我们可以开始了。
2是 系统的 orde r.
我们有一个2 x 2矩阵、其等级为2。
这是可 控制性矩阵。
因此、我们仍然很好。
现在是可观察的 Matri 坐标轴2 x 2、它有一个秩。
现在、我们也开始 了可观察性。
因此您可能会遇到问题。
这些问题往往 会降低可控性
简称 WCT。
因此 、我们在本次课程中几乎没有遇到过这种情况。
然后、我们将 准时地点餐。
现在、我要在 GTO 中使用的系统非常一致
今天下午 、对于教程、
是一个机械系统。
它基于像 这个这样的双重 sma 系统、其中
有两个质量、M 1和 M2、它们在坐着
并在 某种情况下自由滑动。
因此、您可以想象 这两个质量
金属块或桌子上的某种薄格。
我们可以影响 他们的立场
从 质量 M1的黄昏开始。
当我们这么做时、 很显然 M1将移动。
其位置称为 Y1。
当它移动时、它会 在 M2上施加力、
因为它通过 该弹簧减振器与它耦合
组件
现在、这些 sprin gand 风门值
耦合的情况
耦合非常轻微潮湿。
这意味着、当你在 M1上给它一点细微差别时、
M2将 像这样进行归零、
它将在很 长一段时间内继续执行 lik ethat。
因为 那里有非常轻的阻尼。
那么、现在、如果我构造 它的 da 模型、
就像这样、这可能 会永远地滑动。
因为 没有什么东西可以阻止它。
我所做的是、我已经对 DIN 进行了几个摩擦术语的说明
因此、我 当然不会
你知道 会有摩擦。
这种化石 正在发展
死机有两个原因。
一个是 因为它有点潮湿、
另一个原因是 存在滑动摩擦
这 将最终在这两个质量中获得成功
为了平稳的停止、我 只需给它一个踢。
现在、我 想变量 o finterest 是 Y2。
我想我 在这里的工作就是我
力控制、 施加到 M1的力、
希望专家组 Y2 在我希望的位置。
当然、在 不受控制的无反馈中
情况、某种程度的操作 计、实际上是死算。
但 您将在今天下午晚些时候看到 Ron
控制的应用、
它是令人惊叹的超精确度
使用 gof M2的位置、即使有
它们 之间的间接耦合、
它们之间的轻微阻隔耦合。
现在 、我选择它的原因是
您可以将 此处发生的情况可视化。
它 有一个很好的统计器空间描述。
我将此作为新 版本的书中的附录。
它还可以从 网站下载
附录。
因此、如果 您访问网站和您
查找 该书的版本、
如果您不 想购买这本书、
您实际上可以在 此处重新创建附录、
附录 E、它实际上为 您编写了所有这些内容。
这是 PDF 格式的电子附录、
欢迎 您下载。
而不进行详细 介绍
是运动方程。
这就是这个空间方程的样子。
这是二阶的。
您有 一个4x4系统矩阵。
什么 情况下发生呢?
太好了!
[INAUDIBLE]?
抱歉。
您在附录中给出了它。
这里有一些 mor 电子信息。
我能不能事后跟你谈谈这件事吗?
因为我没有 完整的推导
而设计。
这将有所帮助。
是的,可行。
是的。
我可能应该这么做。
我还没有完成 整个推导过程
而设计。
但方程 中的"sher"几乎是正确的。
它们 不是完全正确的原因就是这样。
我也可以告诉您。
看到、我刚刚应用 了牛顿的第二定律
以获取这两项。
这里也有一个摩擦力。
因为这是 关于运动的电子方程
第一个质量的值、其为 输入力 u
其中涉及的内容。
我已经将 状态指定为
第一 块块块块块块块块的位置及其导数。
那么、这是第一 个质量的速度 DOF、
以及 secon dmass 的位置及其导数。
因此、当我为 x2点形成电子方程时、
乘以加速 因子 nx2点等于所有该批次。
问题是 这里的 mas sterm 出现在左侧。
因此、您将会遵守 这些其他条款
乘 以 M1除以除法、
左 侧有 x2点、如果您愿意、
控制器,即这里的 EC。
而薄 的 gthat 出错了
我忘记 了将该项除以 M1。
那么、在 这里的方程上、这不应该是1。
这应该是1除以 M1、对吧?
因此、无论如何、我在 六个月前发布了该内容。
我了解 了这种情况的结果。
因为有 七或八个像
附录 E 中的不同部分和所有拓扑。
我们的到来 非常漂亮。
然后我开始了 BAC KTO
在我发布了 Dar ning 之后、我查看了它。
天哪!
我忘记了 M1。
您知道 我为什么要离开它?
因为 M1是1千克。
因此 、我在人生中有一次很幸运。
因此 M1是1千克。
好。
现在、让我们快速 学习本教程、
您将看到该 系统的行为、
或没有行为、具体取决于 您的行为定义。
好的,
好了。
所以、我们要做的 是非常精细的非常细化的 gery。
我已在脚本中更正了它。
在这里、我们将使用 SS 函数创建模式焊盘
以创建状态空间模型。
就是这个。
现在、我要做的是 执行模式分解
就像 我之前所做的那样。
我们将看到 模体的外观。
现在、它是一个拥有 一整套特征器的系统。
因为我 现在有一个完整的对角线模式矩阵。
但您已经可以使用 这两个特征值
非常复杂。
因为大多数 esmall 实际组件、
但想象中的分量 非常虚幻。
因此 、您在这里有一个较低的振荡。
我们可以 从中看到的
在第三种模式下存在一个非常小的数字。
这可能意味 着系统不稳定。
但这并不理想。
这低至 MATLAB 的分子分辨率。
这是一个0 eigenvalue。
我们有一 个模式线性输入矩阵
它包含一组复杂的术语。
因此、我 可以控制系统、这很好。
您可能会想象 它是什么样的系统。
和模型 outpu tmatrix 类似
一个复杂的术语集。
因此、它也是 一个不可伺服系统。
到目前为止一切顺利。
我们可以像 以前一样,以同样的方式来核实这一点。
那么、让我来证明 它是可控的
它很复杂。
现在、我要做的是 不执行初始条件
评估它的稳态响应。
我将从 x 矢量中转到 t*、它
因为这里有 四种状态。
我将从 该状态中提取第一状态和第三状态。
现在、我已经在其中添加 了这两者之间的初始分色。
因此、这个 y0 更远、
这表示初始 化两个质量
被距离隔开。
我想我使用 大约一个仪表。
它是一 个非常好的双系统、这个。
那么、当我将其添加到该位置、 然后减去第一个
从第三种模式 中、我从 Y2减去 Y1、
并添加初 始偏移。
因此、这将为 LME 分色
质量的影响。
当我运行它时、 您会看到 EIT 是一个振荡系统
确实。
这是一个曲线。
但您将 看到它会下降
我们开始控制它。
总数值非常高。
因为你给了我 一个微移、它将会运行
就像那样。
这就是 EN/UVLO 引脚。
让我 第二次运行 BAC KA、然后向您展示
我使用了什么初始条件。
这个矢量、我在这里 对第一个位置质量进行了调节
稍微偏右一点、 这是一个正向。
第二个是 左侧的易碎位。
因此、我稍微压缩了一下 sprin GA、
然后放开。
因此、这 种平装的东西压缩了它
为 10 伏或类似的电压,
它会停止所有该运动。
这是 IC。
现在、我们将绘制 单个质量位置。
这是 所涉及的绝对的排列。
因为我 将 Y2的开始考虑在内。
Y0被添加到 Y2中。
在 我们应用该测试时、您将看到行为是如何的。
好了。
那么,这是 ROM。
它要重得多、 而且它的 SGOT 是一个更大的摩擦
大电压系数引起的。
它的 衰减速度非常快。
这是质量 M2 、它受到影响
到更大的程度。
很好。
这 两种情况下会发生什么情况
会在 该幻灯片上缓慢地摆动
Way:
他们在 幻灯片上进一步休息了大约法米
比他们开始时要好很多。
因此、我想您可以通过 执行 BOOING 来实现这一目的、就像这样、
它将 稍微振荡一点。
然后它最终进入 GTO 移动并休息。
就是这样。
如果 我们有如此倾向、
构建该图的波特图。
为此、我们启用 了传递函数
表示
好,就是这。
现在、这证明 存在 SAN 集成。
因此、极小 的 leigenvalue 为0。
然后、我得到 了共轭偶极
和 一个实极点和一个实0。
所有这些东西都可以 在波特图中进行初始化、
样子的拓扑。
因此、我们有一个积分器 、负90度、然后
有一 个共轭共轭极对、它
提供了这个和那个。
然后、这里有一个极点、 真正的极点和一个真正的0
在这里的某个位置。
这些是校验器的校验器。
我们将 更详细地进行检查
此常见问题解答
现在 剩下的是唯一一个细牙
是我最喜欢的部分 、即测验。
类似 矩阵有什么共同之处?
它们相似吗?
因此、它们 是通用的。
[INAUDIBLE]?
是的、它们确实如此。
是的、它们确实具有 名称值的数量
帧周期和帧数。
这不是 我要找的答案。
但这是一个很好的答案。
我 要寻找的答案是他们
用 二表示 Sam 的系统化
不同的坐标系。
但 你绝对是对这种情况的。
在过去,这主要依赖串行总线
模式表示法的两个优点。
我想此时--
简单
您是对的、简化。
从输入 和输出到输出的路径
可视化效果要明显得多。
[听不清]
对,是的。
因此、由于 我们刚才所说的第一个属性、
证明其正确性。
可观察性、 以及可检测性
10K 欧姆的电阻器。
所有这些东西 都更容易实现可视化
在构建 可控制性矩阵时、
例如 ,寻找一个排名。
因此 、对这些内容进行视觉化要容易得多。
对于离散时间系统、内部稳定情况如何?
[听不清]
您处于稳定状态。
说得对。
稳态输出。
因此、内部稳定性、请调用 另一个名称。
Michelle 知道、它具有 有限的输入、有限的状态。
那么、只要输入受 限、状态是否受限?
如果是、它具有边界 输入受限状态、
或内部稳定性。
这种离散时间会怎么样?
那么 CMTI 呢?
我们对系统的看法是什么
它是否具有内部稳定性?
对我来说、内部稳定性确实 是一个错误。
输入怎么样呢?
稳定。
特征值必须是什么?
[听不清]
对。
它将小于1 、或者如果它具有 Lyapunov 稳定、
它必须是 Equa LTO 1或更少该1。
是的。
系统是什么时候- 我刚才告诉过您。
离散 时间系统何时稳定 ISL?
还记得这是什么意思吗?
从 Lyapunov 的角度来看、它是稳定的
当 eigenvalue 剃须一个幅度时
大于或等于 1
因为实际上严格地说 是 Lyapunov 稳定性
还包括渐近 稳定性。
我们如何确定 给定的状态空间
是否在工作。
我为您提供了两种方法。
第一种甲基甲基甲 基甲基甲基甲基甲基甲基胺
模式分解。
我们对铁蛋白模式分解有何看法?
[听不清]
是的。
是的。
模型输出 Matri x 中没有0列。
模式输出矩阵的每个列、
它们是伽马1、 伽马2、伽马3。
每个伽马耦合的对流二极管都朝向输出。
因此、只要这些 gammas 都不是0、
你知道所有 的表情都是通过耦合的。
因此 系统是可以观察到的。
还有一个测试。
[听不清]
是的。
您构建了 可观察性矩阵 Q
它是 C 转置、 转置、C 转置、
这些分区。
它应该具有 N 的全排名
观察性矩阵。
因此 、有两种不同的方法来确定它。
太棒了。
如何观察 可控制的规范表单
相关
我要找一个词。
双性。
它们是彼此的双重结构。
我 通过转置将系统矩阵相关联。
可见的系统 mmatrix、OCF 矩阵
是 CSF 系统矩阵的转置。
然后、您有 可控制的 B 矩阵
是 C 矩阵的转置、
观测 用例、反之亦然。
是的。
可观察性是 我一直在寻找的字。
我将为您提供该值。
QFN/SON 是什么?
它是什么?
它与 状态矢量的大小有关。
它只是 一个具有最小尺寸的系统
向量的
这就是它的样子、 换句话说、就是很大的尺寸。
与 FRAM 有什么不同?”
和 ARM™
[听不清]
是的。
那么、可检测性-是的。
我知道您的意思。
解决了可检测性问题
不稳定模式。
这意味着您可以 通过观察来检测不稳定性
输出端发生的情况。
现在、我们将 花一点时间吃午餐。
但在我们这么做之前 、我要感谢您
在 过去三小时内引起您的注意。
因为这是一项艰巨的工作。
它似乎很抽象。
其中许多是数学运算。
它看起来不像我 在做任何真正的事情。
但今天下午 、请回来。
因为我们 将获取这些信息
要控制双质量系统等系统、
飞行控制器等令人兴奋的东西。
我们以 非常真实的方式使用该信息。
所有这些东西对于 今天下午的到来都很重要。
因此 、对于那些从 TI 外部加入的引信、
我们在回退时看到了一些袋子
吃午餐。
我们将 在1点处恢复、
请重写 第7章。
手机看
扫码用手机观看
 视频简介
视频简介
线性系统的性质
所属课程:空间控制系列视频
发布时间:2022.08.02
视频集数:4
本节视频时长:01:29:32
该部分主要讲述了稳定性、相图、可控性和可观测性、模态分解。
 视频简介
视频简介