电源管理
最新课程
- LP-MSPM0G3507 按键输入基础:基于计时器的短按检测
- MSPM0G 系列 MCU 时钟配置:在 LED 闪烁的情况下动手操作
- Code Composer Studio™ v20 入门
- 双 DMA 正弦波环回:在 MSPM0G 上实现从 DAC 生成到 ADC 捕捉
- MSPM0G3507 动态 CRC 配置和实时验证
- 视频系列:tiarmclang 编译器
- 汽车应用中的 Jacinto™ 7 处理器
- 可以在 2 分钟内实现无线基础设施应用
- TI 超声成像系统电源方案介绍
- TI 连续血糖监测(CGM)方案介绍
热门课程
1.2 电场基本概念
为了更好地理解电磁兼容的问题
那么我们简单地复习一下
电场的基本概念
电场是由库仑定律来约束的
那么在1600年
英国物理学家吉尔伯特他就发现
用毛皮摩擦琥珀后会产生静电
会吸引小物体
那么他就把这种现象呢
提出了一个电的概念
那么1733年法国物理学家杜飞
他又发现了这个有的时候是吸引电荷
有的时候是排斥的
所以他就把这两个相反的东西呢
把它叫做正电荷和负电荷
那么这个是我们对电最原始的一个认识
那么到了1875年
法国物理学家库仑
他通过一个著名的纽称实验
就发现了电荷之间
存在着力的大小规律是什么样
那么我们就把这个呢叫做库伦定律
库伦定律说什么呢
就在真空中
两个静止点电荷之间的相互作用力
它是与距离的平方成反比的
与两个电量的乘积成正比的
这是它的大小
它的方向呢
作用力的方向是在它们的连线上
如果两个电荷同名它们就相斥
如果两个电荷异名
它们就相吸
那么这个规律呢
是我们电学发展史上的
第一个定量的规律
它的作用是非常重要的
那么这个定律的描述
用一个数学表达式就是这样一个公式
我们把叫做库仑定律
力的单位是 牛顿
电荷的单位呢是 库伦
那么这个是它的标准化以后的
K 的一个单位的表达
那么我们怎么知道空间中存在着电场呢
那么就用一个受试电荷
来看看空间中是否
这个受试电荷在空间中
是否存在力的作用
如果有力那么就说这个地方存在着场
存在着电场
那么力的大
力的大小就决定了
这个电场强度的大小
方向就决定了电场强度的方向
所以说电场强度是这么定义的
在电场中某个位置上的受试电荷
所受到的电场作用力
与受试电荷的一个比值
也就是说单位电荷在空间中
它所受到的电场力的大小
就把它定义为电场强度
那为什么还要定义成
当受试电荷趋向于零时的极限呢
那么这个是一个数学上的表达
也就是说我这个受试电荷
放到这个电场中以后它很小很小
它不会影响原来电场的分布
是这样的意思
所以呢根据电场强度的定义
那么就得到了这样的一个表达式
这个 f 就是力的大小
这个 q' 就是这个受试电荷
它们的比值就是电场强度
那么根据这个呢
我们就可以得到空间中任意一个点
它的电场强度的大小
那么我们来看看
我们怎么描述
这个空间中存在的电场呢
那么就提出了一种图示的办法
首先是一个电场的电场线
也叫做电力线
那么电场线电力线怎么定义呢
它是人为的在电场中构造出的一些线
那么满足线上各点的切线
比如说这一点
它的切线方向与电场强度方向一致
也就是说我这个红线
如果是电场线的话
那么在这一点它的切线方向
与电场强度的方向是一致的
这个规定它的方向
电场线的疏密程度
就与电场强度的大小成比例
也就是说这里的电场线越密
表示的电场强度越大
那么这种定义的数学表达式
就是电场强度×乘 DL
DL 就是这一条电力线
它的×乘会等于0
那么它的特性是什么呢
有四个特性
一个电场矢量 E 在空间点的方向
即为电场线的切线方向
这是它的定义
对于垂直于场线的曲面
通过单位面积的场线数目
正比于该区域电场的强度
这也是定义 表示了它的大小
1 表示方向 2 表示大小
第三场线一定始于正电荷
而止于负电荷
也就是说我们的电场线是
起始于正电荷
终止于负电荷
这个无穷远也是一个点
所以说电力线一定是有始有终
有头有尾的
第四个场线不可能彼此相交
否则的话在这一焦点上
就会有两个不同方向的电场强度
这是不可能的
所以呢场线不可能彼此相交
那么这张图呢
就简单的画出了一个
正电荷和负电荷
在自由空间里面所产生的电力线
那么这些线呢就是电力线
那么这个箭头呢
就表示电力线的一个方向
那么比如说这个区域
电力线比较密
那么就表示电场强度比较大
在这个区域电力线比较稀
就表示电场强度比较小
那么这样子就把我们这个电场的分布呢
很形象地表达出来
那么我们再来看一个电位的概念
首先我们来说电位差
电位差是什么定义呢
也就是说单位电荷或者说电荷 q'
从 A 点移动到 B 点
它所做的功与这个电荷的比值
也就是说单位电荷
从 A 点移动到 B 点所做的功
那么这个功就是能量差
那么能量是等于什么呢
是等于力乘上位移
那我就说 A 点到 B 点的功
就等于 A 点到 B 点力的积分
那么力又等于什么呢
力是电荷乘上电场强度
那么就得到这样一个公式
那么根据这个电位差的定义
让我们定义 A B 两点的电位差
就是等于单位电荷
把 q' 除掉了
那就等于这个定义
那么在这个定义下
我们就定义出一个电位的概念
电位是什么
是 A 点到某一点的电位差
那么如果我们设这个某一点
也就是 O 点的电位为零的话
也就是它的参考电位的话
那么这个呢
就把它定义为 A 点的电位
一个是电位差
一个是电位
那么两者是不一样的
那么电位一定是针对
参考电位而言的
所以电位本质上
就是以参考电位为参考点的电位差
那么这样子呢
我们可以得到 UAB
就可以等于从A到B的积分
然后呢把分解为A到零
零到B点是吧
那么零到B可以写成负的B到零
那么这个呢就是 ΦA 这个呢就是 ΦB
所以两者的电位差
A B 那这个电位差
就等于 A 点的电位减掉 B 点电位
这个是一个很基本的概念
同时呢我们还能看到
电场强度与电位的关系是这个
那么这是根据这个前面的定义来的
也就是说空间任意一点的电场强度
它等于该点电位函数梯度的负值
Φ 这就表示梯度
这个里面表示梯度
即电场强度总是由高电位指向低电位
这就是我们电位的一个基本概念
那么如何来描述这个电位的空间分布呢
那么就采用一种电场的等位线
或者等位面的概念
它怎么定义呢
具有相同电位的面
或者线就称为等位面或者等位线
它的数学表达式就是 E 的矢量
点乘 DL 是等于 0 的
那就表示 E 在整个 L 线上
它都是相同的电位的
那么这个等位线的特点什么呢
1 电场线垂直于等位面
也就是它是正交的
并且由高电势指向低电势
就是高电位指向低电位
那么这条线呢
这些线呢就是等位线
这个是电力线
这是等位线
他们呢是正交的
他们是正交的
第二电场沿等位面的切线分量为零
第三个沿等位面移动电荷不做功
因为电荷的移动
如果沿着是等位面动的话
它就不会做功
因为等位面上面的电位都是一样的
它没有电位差就没有电场强度
也就是说电荷沿着
没有电场强度的方向走
它是不做功的
这就是我们讲电场的等位面
那么这个图呢
就更形象的看出了
两个正负电荷之间
它们电位的一个分布情况
它是呈圆形的一个分布规律
那么我们再来看看电场的两个基本特性
一个呢叫做电场的环路定律
也就是说电场的环路定律
那么由于电荷 Q
从A点移动到B点所作的功
可以用这个来表达
也就是 UAB 啦 那电位差啦
它可以写成这个式子
因为 E 是等于这一堆
那么我们经过数学推导
这个具体大家可以看一看
它会等于这个东西
会等于这个那什么意思呢
也就是说场强的线积分
或者说电场力所做的功
它是与积分路径是无关的
仅与起点和终点的位置有关
也就是说你从 A 点移到 B 点
你走的是这条路
它是得到的是
rA rB 这个式子
你从另外一条路走
它也是 rA rB
它只跟终点的位置有关
而与中间的走的过程是无关的
这是一个主要的一个特点
第二个 在电场中
电荷沿任意闭合路径移动回原点
也就是说你从起点开始
到外面转了一圈回来
再回到这个起点
那么电场力所做的功一定是零
也就是说电场强度的环路线积分是环路了
是闭合的环路的线积分恒等于0
那么数学表达出来
就是 E 沿着一个闭合路径
这地方是一个闭合路径的线积分它等于0
那这就是说表示静电场是无旋场
它是保守场
它的微分形式是这样子
那么根据场论的定义
它的旋度就这样定义
它的旋度由于这项等于 0 了
所以它的旋度等于 0
这它的积分形式
也就是说保守场
静电场它是无旋场
就是这样的一个意思了
那我们再来看看他的第二个定律
是通量定理
也就是说看它的电通量
那么我们怎么来定义电通量呢
通量就是电场强度乘上介电常数
就是它的电通量
那么我们来看看电通量的一些基本特征
我们先看看这样的一个 S 面
它对 q 点的电通量是怎么定义呢
就是这样的一个积分
D 点乘 S 这个表示一个微元
表示这个面积上面的一个小微元
ds 它沿着整个大 S 的一个积分
就叫做S面
这个S面对q点所张的一个立体角
它是等于这个东西
那么 D·DS 呢又可以写成这个东西
这个 R0 R0 这个矢量是表示D的矢量
N0 这个矢量
表示这个面的法向单位矢量
那么经过这样推导呢
就能够得到这样的一个公式
也就是说S这个面积
它的一个通量的面积分是等于
q/4Π q 就是电荷
以及乘上一个Ω
那么这个Ω呢叫做这个S面
对 q 点所张的立体角
就是这个是立体角
那么根据这样的一个概念呢
我们知道由于任意封闭面
对曲面类的一点所张的立体角都是 4Π
所以通过该曲面 S 的总的电通量
这个是闭合面了
一定会等于 q
对于二维的闭合面
比如说这一个电荷
这是一个二维的闭合面
那么它的立体角算作 2Π
如果是一个立体的闭合面
那么它所张的立体角呢就是 4Π
所以呢就得到这样的一个公式
那么这个就表示什么呢
表示电场是有源的
他是从点电荷 q 往外面发散的
所以它的积分形式就是这样一个表达式
也就说 D 沿着一个闭合路径的面积分
它会等于它里面的所包含的电荷量
不管你这个电荷所在的位置是什么
只要在这个闭合面的内部
它都会等于 q
那如果在外部呢
也就是说我如果电荷
是在这个包围闭合面的外部
那么它的通量的面积分就会等于 0
因为它里面没有电荷
那么把这个积分形式
把它变成微分
微分形式就得到 D 的散度等于电荷密度
因为这个电荷量除上上面这项的电荷量
电荷量除上体积就是这一点的电荷密度
所以把它叫做电场的微分形式
就是电通量的微分形式
所以这两个定律
一个是前面的这个环路定律
一个是高斯定理或者说通量定理
那就把我们整个电场的特性呢描述出来了
也就是无旋场跟有源厂这两个最基本的定律
那么这一节我们说到这里
谢谢
-
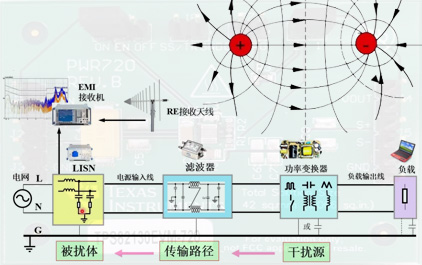 未学习 1.1 功率变换器的电磁干扰特性
未学习 1.1 功率变换器的电磁干扰特性
-
 未学习 1.2 电场基本概念
未学习 1.2 电场基本概念
-
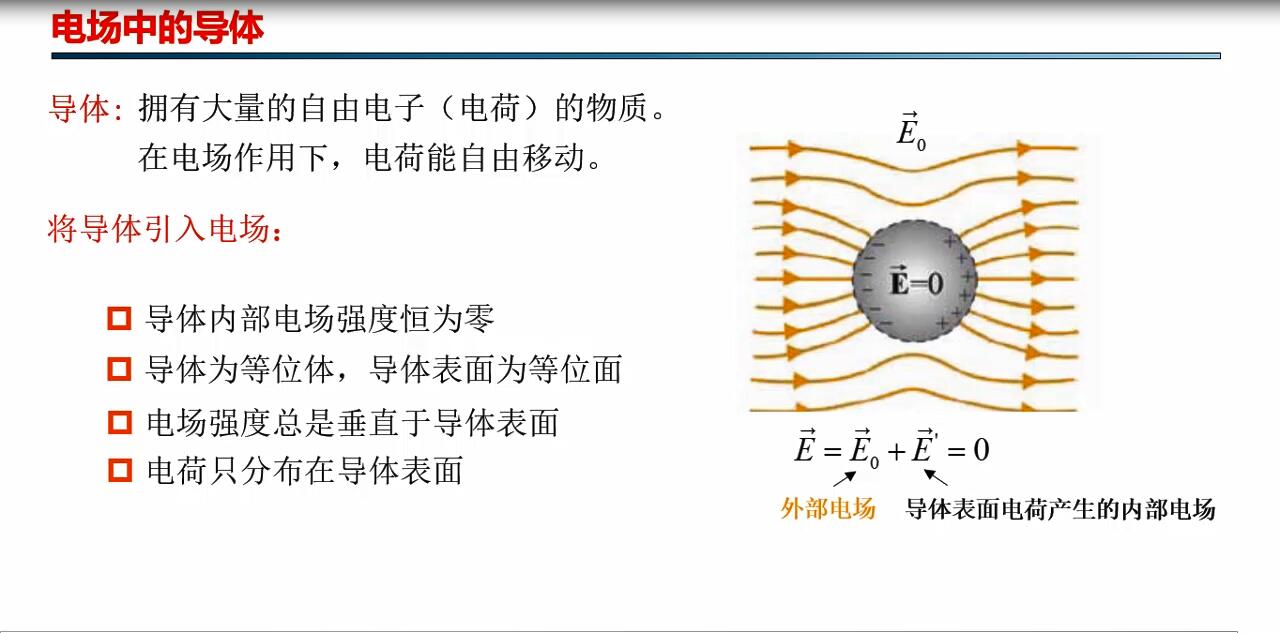 未学习 1.3 电场中的导体、电容、电场屏蔽
未学习 1.3 电场中的导体、电容、电场屏蔽
-
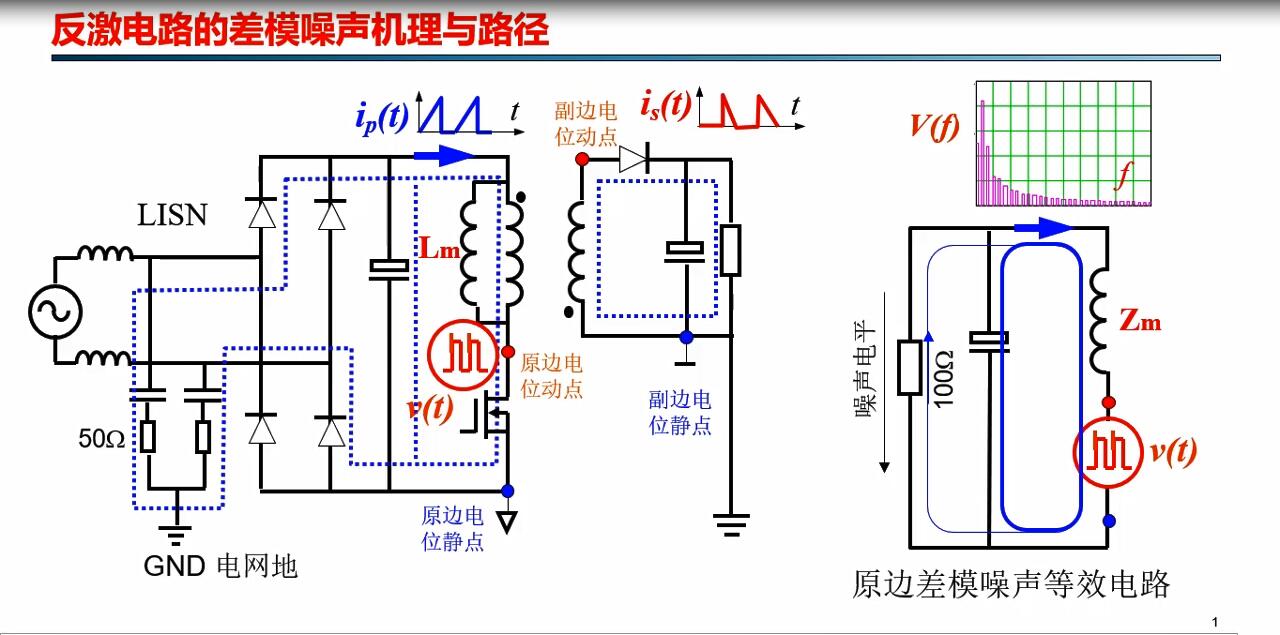 未学习 1.4 差模传导电磁干扰噪声分析
未学习 1.4 差模传导电磁干扰噪声分析
-
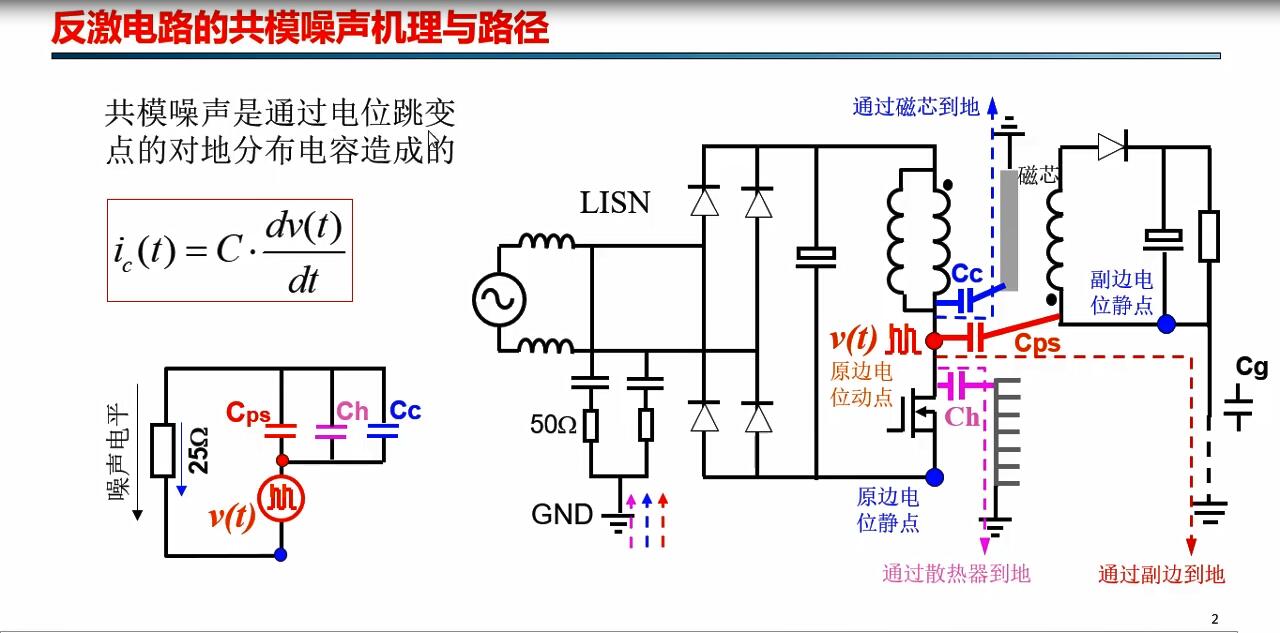 未学习 1.5 共模传导电磁干扰噪声分析
未学习 1.5 共模传导电磁干扰噪声分析
-
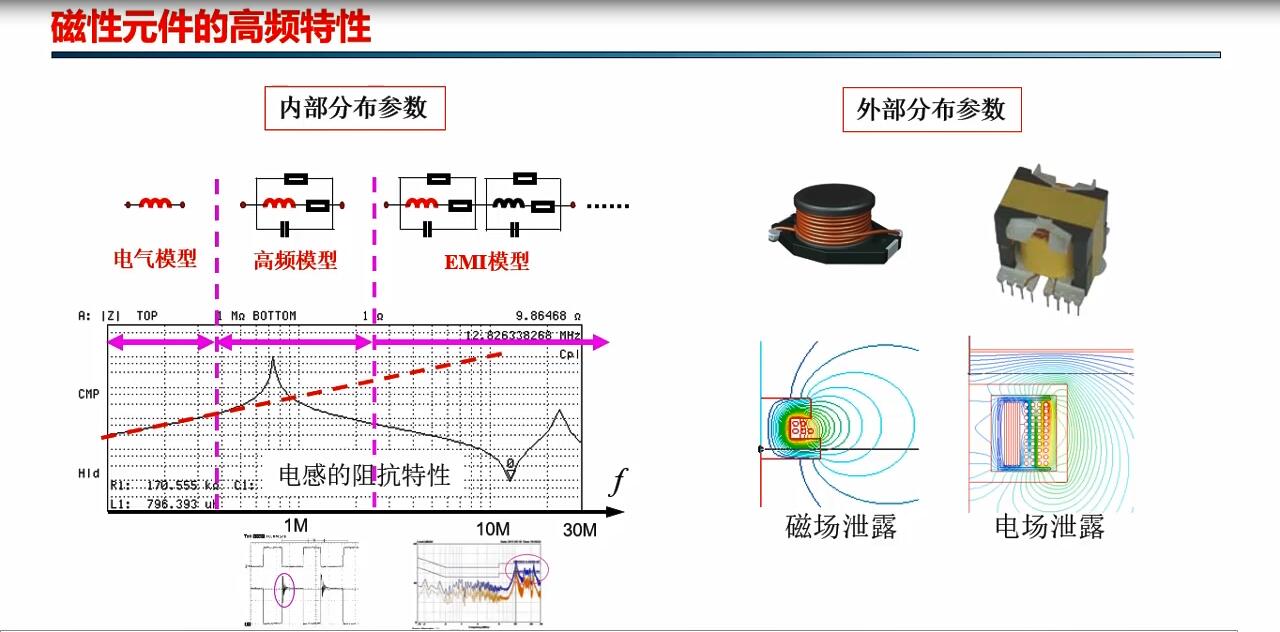 未学习 1.6 磁性元件分布参数及其高频特性
未学习 1.6 磁性元件分布参数及其高频特性
-
 未学习 1.7 EMI滤波器与插入损耗
未学习 1.7 EMI滤波器与插入损耗
-
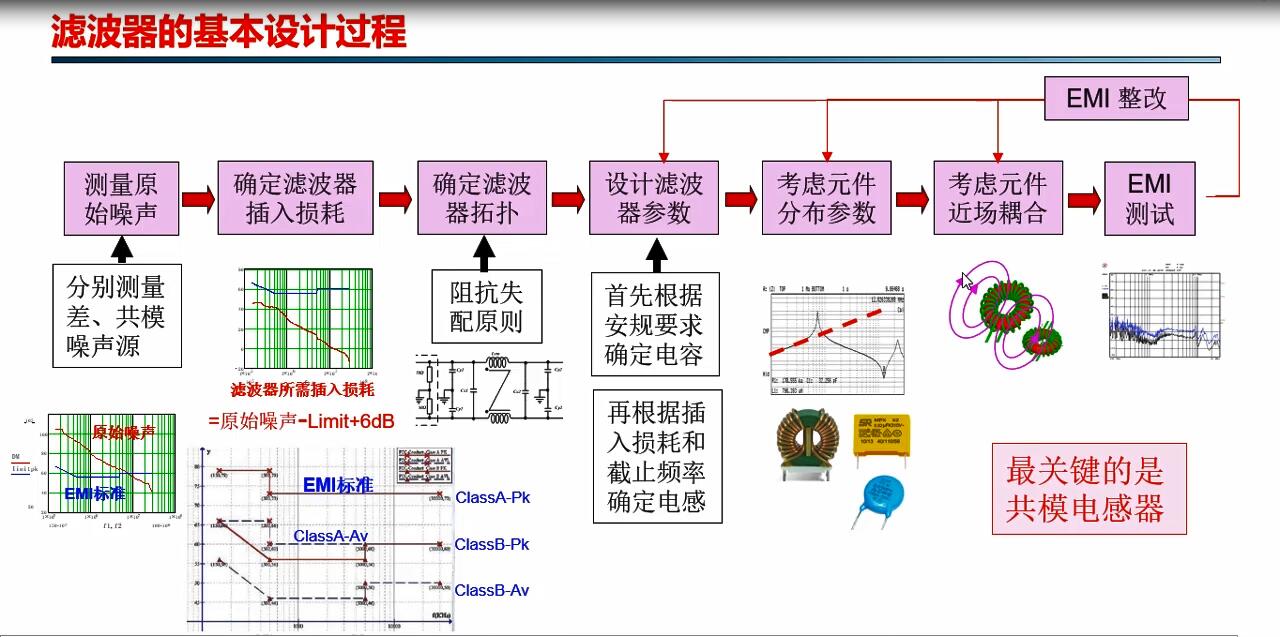 未学习 1.8 共模滤波电感器
未学习 1.8 共模滤波电感器