5.2 TI 高精度实验室 - 带宽 2
Loading the player...
将在30s后自动为您播放下一课程
大家好 欢迎来到 TI Precision Labs 德州仪器高精度实验室 本次视频将介绍 运算放大器的 Bandwidth 带宽的第二部分 我们将探讨 open loop gain 开环回路增益 closed loop gain 闭环回路增益 gain bandwidth product 增益带宽积 Quiescent Current 静态电流与带宽的关系 也将仿真电路的带宽 并验证我们的计算结果 运算放大器的开环回路增益 或 Aol 代表由运算放大器 施加到输入端电压差的增益 运算放大器的 Aol 是无限大 然而真实世界的运算放大器 有超过 100 万 V/V 或 120dB 的开环回路增益 为了使一个放大器稳定 Negative feedback 负回授是必要的 可以经由 Rf 和 R1 来实现 有时被称为闭合回路 Rf 和 R1 代表 β 的网络 或回授系数 β 是经由测量 Vout 回授到运算放大器的 反相输入端变化来求得 在这个电路中我们看到 Rf 和 R1 产生一个电压分压器 因此 β=R1/(R1+Rf) 除运算放大器的开环回路增益 我们有所谓的闭环回路增益或 Acl 该方程 Acl=Aol/(1+Aolβ) 其中的 Aolβ 被称为回路增益 如图所示 这个方程式可以重新整理 闭环回路这一方程式可以简化 是由于有非常大的回路增益或 Aolβ 纵观回路增益公式可以看出 当 Aolβ 增加到无限大 你可以忽略分母中的 1 公式可简化为 Aol/Aolβ 将分子分母的 Aol 相消可得到 1/β 代入 β 可以得到 1+Rf/R1 的 闭环回路增益 这是一个常见的 none inverting 同相放大器闭环回路增益公式 重点是这个公式 只适用于开环回路增益非常高时 稍后我们将看到 当开环回路增益低会发生什么事情 然而在现实世界中 运算放大器的开环回路增益 具有低频的 dominant pole 主极点 如图所示 可以被看做是一个 RC filter滤波器 此仿真描绘了真实世界 运算放大器开环回路增益 在直流或低频 Aol 是非常大的 在这种情况下 它是 120dB 或 100万V/V 随着频率的增加 Aol 以 -20dB/dec 的速率降低 我们看到在 10MHz 时 开环回路增益为 0dB 或 1V/V 现在我们明白开环回路增益 会随着频率降低 此现象如何影响我们的闭环回路增益呢 回想一下 Aolβ 被称为回路增益 如果我们绘制了开环回路增益和 1/β 在对数轴 回路增益为两条曲线之间的差值 数学证明回路增益是 Aol 减掉 1/β 如底下的方程式所示 在这个例子中 1/β 为水平虚线在 20dB 注意 闭环回路增益在低频时为 1/β 在高频时为 Aol 曲线 还要注意在这 1/β 曲线和 Aol 曲线交错的点 是闭环回路带宽 让我们更深入地看看为什么闭环回路增益 在低频时为 1/β 而在高频时为 Aol 在低频时回路增益或 Aolβ 很大 请注意闭环回路增益为 Aol/(1+Aolβ) 所以对于较大 Aolβ 可以忽略 1 这一项 公式可简化为 Aol/Aolβ 将分子分母的 Aol 相消可得 1/β 在这种情况下 1/β 是一个熟悉的同相放大器增益方程式 1/β 是一个熟悉的同相放大器增益方程式 值为1+Rf/R1 在高频时 Aolβ 很小 请注意 闭环回路增益为 Aol/(1+Aolβ) 所以对于小的 Aolβ 值 就可以忽略 Aolβ 这样一来就只剩下 Aol/1 或者说就是 Aol 因此当 Aolβ 变小 闭环回路增益跟随 Aol 曲线 我们定义的电路的带宽为 1/β 和 Aol 曲线相交的频率 因此运算放大器数据表中 Aol 曲线可以近似到电路所需的闭环回路增益带宽 然而请注意 X 轴是对数的 因此以图形方式选定的带宽可能不够精确 另一种方法来确定带宽 是使用运算放大器数据表中的增益带宽积产品规格 增益带宽积是线性增益和带宽的乘积 因此在给定两个变数中的一个 可以得到另外一个解 例如让我们计算 OPA827 在 100V/V 的带宽吧 从数据表我们可以得知 增益带宽积为 22MHz 为求解带宽 从增益带宽公式告诉我们 带宽为增益带宽积除以线性增益 将 OPA827 增益带宽积 22MHz/100V/V 的增益 可以得到 220kHz 带宽 此计算可由观察数据表中 OPA827 开环回路增益来验证 如果画一条水平线在 100V/V 或 40dB 的闭环回路增益 直到它相交 Aol 我们找到了相应的带宽 大约为 200kHz 可以注意到 通过计算我们发现 带宽为 220kHz 它解决了图解可能错误地解释带宽为 200kHz 请注意计算出的带宽 须当 Aol 局限于 -20dB/dec 的速率下降才是有效的 虽然大部分的运算放大器都符合 但也有些特定的增益带宽积是有限的范围 此外考虑到数据表有增益带宽积 和 Aol 曲线的典型值 通常可以预期该值在室温下的变异数高达± 30% 在规定的温度范围外 可能有附加正负 30% 误差的变化 因此当考虑到放大器的带宽时 建议设计时保留您的设计裕度 现在让我们与 TINA-TI 仿真做比较 这里我们将一个 OPA140 设计为同相放大器组态 100V/V 或是 40dB 的闭环回路增益 该 OPA140 具有 11MHz 的增益带宽积 代入我们的闭环回路增益 100V/V 可以求出带宽为110kHz 在这里我们仿真的电路的闭环回路带宽 在 -3dB 点或 37dB 仿真带宽为 118kHz 虽然不完全一样 但我们计算和仿真结果是正相关的 最后让我们来看一下 一系列 TI 运算放大器的增益带宽 和其相对应的静态电流 Iq 此页我们列出增益带宽范围 从 12kHz 到 600MHz 放大器 OPA369 是一个非常低带宽的放大器 该电路是特别设计为非常低的静态电流 仅有 0.8uA 称为微功率电路 1MHz 为普遍放大器的带宽范围 如 OPA277 而 OPA350 和 OPA211 则具有更宽的带宽 以方便驱动 A/D 转换器 和其他高带宽应用 对非常高速应用中 可使用如 OPA835 和 OPA847 在一般情况下较宽的带宽运算放大器 需要较多的静态电流 不过有例外如 OPA835 那么为什么带宽和静态电流有关联 让我们来看看双极性和 CMOS 晶体管的物理关系 请注意 这里不是要深入理解晶体管理论 来了解放大器的带宽 这里的关键是 表示放大器带宽和静态电流间的物理原理 观察双极晶体管和 MOSFET 的 Transductions 转导或电流增益 可以看出 collector 基极和 drain 漏极 电流的直接关系 转导取倒数可得阻抗或 rgm rgm 是运算放大器内部第一级的动态输出阻抗 此输出阻抗驱动米勒电容 Cc rgm 和 Cc 的串联组合形成一个低通滤波器 该低通滤波器的主极点产生放大器内部的带宽 事实上你可以看到第三个方程式 是 RC 带宽公式 BW=2πRC 在最后的方程式 我们代入原有的 gm 公式来说明 gm 带宽的关联 其显示增加电流消耗 直接增加双极性运算放大器的带宽 但是如果是 MOSFET 带宽将依漏极电流平方根的比例增加 所以相较于双极晶体管 MOSFET 需要增加更大的电流来增加带宽 总结 这个视频讨论开环回路和闭环回路增益 增益带宽积 静态电流与带宽 我们还仿真电路的带宽 并显示带宽与我们计算结果的关联性 感谢您的时间 请尝试测验来检视对这个视频内容的理解吧
大家好 欢迎来到 TI Precision Labs 德州仪器高精度实验室 本次视频将介绍 运算放大器的 Bandwidth 带宽的第二部分 我们将探讨 open loop gain 开环回路增益 closed loop gain 闭环回路增益 gain bandwidth product 增益带宽积 Quiescent Current 静态电流与带宽的关系 也将仿真电路的带宽 并验证我们的计算结果 运算放大器的开环回路增益 或 Aol 代表由运算放大器 施加到输入端电压差的增益 运算放大器的 Aol 是无限大 然而真实世界的运算放大器 有超过 100 万 V/V 或 120dB 的开环回路增益 为了使一个放大器稳定 Negative feedback 负回授是必要的 可以经由 Rf 和 R1 来实现 有时被称为闭合回路 Rf 和 R1 代表 β 的网络 或回授系数 β 是经由测量 Vout 回授到运算放大器的 反相输入端变化来求得 在这个电路中我们看到 Rf 和 R1 产生一个电压分压器 因此 β=R1/(R1+Rf) 除运算放大器的开环回路增益 我们有所谓的闭环回路增益或 Acl 该方程 Acl=Aol/(1+Aolβ) 其中的 Aolβ 被称为回路增益 如图所示 这个方程式可以重新整理 闭环回路这一方程式可以简化 是由于有非常大的回路增益或 Aolβ 纵观回路增益公式可以看出 当 Aolβ 增加到无限大 你可以忽略分母中的 1 公式可简化为 Aol/Aolβ 将分子分母的 Aol 相消可得到 1/β 代入 β 可以得到 1+Rf/R1 的 闭环回路增益 这是一个常见的 none inverting 同相放大器闭环回路增益公式 重点是这个公式 只适用于开环回路增益非常高时 稍后我们将看到 当开环回路增益低会发生什么事情 然而在现实世界中 运算放大器的开环回路增益 具有低频的 dominant pole 主极点 如图所示 可以被看做是一个 RC filter滤波器 此仿真描绘了真实世界 运算放大器开环回路增益 在直流或低频 Aol 是非常大的 在这种情况下 它是 120dB 或 100万V/V 随着频率的增加 Aol 以 -20dB/dec 的速率降低 我们看到在 10MHz 时 开环回路增益为 0dB 或 1V/V 现在我们明白开环回路增益 会随着频率降低 此现象如何影响我们的闭环回路增益呢 回想一下 Aolβ 被称为回路增益 如果我们绘制了开环回路增益和 1/β 在对数轴 回路增益为两条曲线之间的差值 数学证明回路增益是 Aol 减掉 1/β 如底下的方程式所示 在这个例子中 1/β 为水平虚线在 20dB 注意 闭环回路增益在低频时为 1/β 在高频时为 Aol 曲线 还要注意在这 1/β 曲线和 Aol 曲线交错的点 是闭环回路带宽 让我们更深入地看看为什么闭环回路增益 在低频时为 1/β 而在高频时为 Aol 在低频时回路增益或 Aolβ 很大 请注意闭环回路增益为 Aol/(1+Aolβ) 所以对于较大 Aolβ 可以忽略 1 这一项 公式可简化为 Aol/Aolβ 将分子分母的 Aol 相消可得 1/β 在这种情况下 1/β 是一个熟悉的同相放大器增益方程式 1/β 是一个熟悉的同相放大器增益方程式 值为1+Rf/R1 在高频时 Aolβ 很小 请注意 闭环回路增益为 Aol/(1+Aolβ) 所以对于小的 Aolβ 值 就可以忽略 Aolβ 这样一来就只剩下 Aol/1 或者说就是 Aol 因此当 Aolβ 变小 闭环回路增益跟随 Aol 曲线 我们定义的电路的带宽为 1/β 和 Aol 曲线相交的频率 因此运算放大器数据表中 Aol 曲线可以近似到电路所需的闭环回路增益带宽 然而请注意 X 轴是对数的 因此以图形方式选定的带宽可能不够精确 另一种方法来确定带宽 是使用运算放大器数据表中的增益带宽积产品规格 增益带宽积是线性增益和带宽的乘积 因此在给定两个变数中的一个 可以得到另外一个解 例如让我们计算 OPA827 在 100V/V 的带宽吧 从数据表我们可以得知 增益带宽积为 22MHz 为求解带宽 从增益带宽公式告诉我们 带宽为增益带宽积除以线性增益 将 OPA827 增益带宽积 22MHz/100V/V 的增益 可以得到 220kHz 带宽 此计算可由观察数据表中 OPA827 开环回路增益来验证 如果画一条水平线在 100V/V 或 40dB 的闭环回路增益 直到它相交 Aol 我们找到了相应的带宽 大约为 200kHz 可以注意到 通过计算我们发现 带宽为 220kHz 它解决了图解可能错误地解释带宽为 200kHz 请注意计算出的带宽 须当 Aol 局限于 -20dB/dec 的速率下降才是有效的 虽然大部分的运算放大器都符合 但也有些特定的增益带宽积是有限的范围 此外考虑到数据表有增益带宽积 和 Aol 曲线的典型值 通常可以预期该值在室温下的变异数高达± 30% 在规定的温度范围外 可能有附加正负 30% 误差的变化 因此当考虑到放大器的带宽时 建议设计时保留您的设计裕度 现在让我们与 TINA-TI 仿真做比较 这里我们将一个 OPA140 设计为同相放大器组态 100V/V 或是 40dB 的闭环回路增益 该 OPA140 具有 11MHz 的增益带宽积 代入我们的闭环回路增益 100V/V 可以求出带宽为110kHz 在这里我们仿真的电路的闭环回路带宽 在 -3dB 点或 37dB 仿真带宽为 118kHz 虽然不完全一样 但我们计算和仿真结果是正相关的 最后让我们来看一下 一系列 TI 运算放大器的增益带宽 和其相对应的静态电流 Iq 此页我们列出增益带宽范围 从 12kHz 到 600MHz 放大器 OPA369 是一个非常低带宽的放大器 该电路是特别设计为非常低的静态电流 仅有 0.8uA 称为微功率电路 1MHz 为普遍放大器的带宽范围 如 OPA277 而 OPA350 和 OPA211 则具有更宽的带宽 以方便驱动 A/D 转换器 和其他高带宽应用 对非常高速应用中 可使用如 OPA835 和 OPA847 在一般情况下较宽的带宽运算放大器 需要较多的静态电流 不过有例外如 OPA835 那么为什么带宽和静态电流有关联 让我们来看看双极性和 CMOS 晶体管的物理关系 请注意 这里不是要深入理解晶体管理论 来了解放大器的带宽 这里的关键是 表示放大器带宽和静态电流间的物理原理 观察双极晶体管和 MOSFET 的 Transductions 转导或电流增益 可以看出 collector 基极和 drain 漏极 电流的直接关系 转导取倒数可得阻抗或 rgm rgm 是运算放大器内部第一级的动态输出阻抗 此输出阻抗驱动米勒电容 Cc rgm 和 Cc 的串联组合形成一个低通滤波器 该低通滤波器的主极点产生放大器内部的带宽 事实上你可以看到第三个方程式 是 RC 带宽公式 BW=2πRC 在最后的方程式 我们代入原有的 gm 公式来说明 gm 带宽的关联 其显示增加电流消耗 直接增加双极性运算放大器的带宽 但是如果是 MOSFET 带宽将依漏极电流平方根的比例增加 所以相较于双极晶体管 MOSFET 需要增加更大的电流来增加带宽 总结 这个视频讨论开环回路和闭环回路增益 增益带宽积 静态电流与带宽 我们还仿真电路的带宽 并显示带宽与我们计算结果的关联性 感谢您的时间 请尝试测验来检视对这个视频内容的理解吧
大家好
欢迎来到 TI Precision Labs
德州仪器高精度实验室
本次视频将介绍
运算放大器的 Bandwidth 带宽的第二部分
我们将探讨 open loop gain
开环回路增益
closed loop gain 闭环回路增益
gain bandwidth product 增益带宽积
Quiescent Current 静态电流与带宽的关系
也将仿真电路的带宽
并验证我们的计算结果
运算放大器的开环回路增益
或 Aol 代表由运算放大器
施加到输入端电压差的增益
运算放大器的 Aol 是无限大
然而真实世界的运算放大器
有超过 100 万 V/V
或 120dB 的开环回路增益
为了使一个放大器稳定
Negative feedback 负回授是必要的
可以经由 Rf 和 R1 来实现
有时被称为闭合回路
Rf 和 R1 代表 β 的网络 或回授系数
β 是经由测量 Vout 回授到运算放大器的
反相输入端变化来求得
在这个电路中我们看到 Rf 和 R1
产生一个电压分压器
因此 β=R1/(R1+Rf)
除运算放大器的开环回路增益
我们有所谓的闭环回路增益或 Acl
该方程 Acl=Aol/(1+Aolβ)
其中的 Aolβ 被称为回路增益
如图所示 这个方程式可以重新整理
闭环回路这一方程式可以简化
是由于有非常大的回路增益或 Aolβ
纵观回路增益公式可以看出
当 Aolβ 增加到无限大
你可以忽略分母中的 1
公式可简化为 Aol/Aolβ
将分子分母的 Aol 相消可得到 1/β
代入 β 可以得到 1+Rf/R1 的
闭环回路增益
这是一个常见的 none inverting
同相放大器闭环回路增益公式
重点是这个公式
只适用于开环回路增益非常高时
稍后我们将看到
当开环回路增益低会发生什么事情
然而在现实世界中
运算放大器的开环回路增益
具有低频的 dominant pole 主极点
如图所示 可以被看做是一个 RC filter滤波器
此仿真描绘了真实世界
运算放大器开环回路增益
在直流或低频 Aol 是非常大的
在这种情况下
它是 120dB 或 100万V/V
随着频率的增加 Aol 以 -20dB/dec 的速率降低
我们看到在 10MHz 时
开环回路增益为 0dB 或 1V/V
现在我们明白开环回路增益
会随着频率降低
此现象如何影响我们的闭环回路增益呢
回想一下 Aolβ 被称为回路增益
如果我们绘制了开环回路增益和 1/β 在对数轴
回路增益为两条曲线之间的差值
数学证明回路增益是 Aol 减掉 1/β
如底下的方程式所示
在这个例子中
1/β 为水平虚线在 20dB
注意 闭环回路增益在低频时为 1/β
在高频时为 Aol 曲线
还要注意在这 1/β 曲线和 Aol 曲线交错的点
是闭环回路带宽
让我们更深入地看看为什么闭环回路增益
在低频时为 1/β
而在高频时为 Aol
在低频时回路增益或 Aolβ 很大
请注意闭环回路增益为
Aol/(1+Aolβ)
所以对于较大 Aolβ
可以忽略 1 这一项
公式可简化为 Aol/Aolβ
将分子分母的 Aol 相消可得 1/β
在这种情况下
1/β 是一个熟悉的同相放大器增益方程式
1/β 是一个熟悉的同相放大器增益方程式
值为1+Rf/R1
在高频时 Aolβ 很小
请注意 闭环回路增益为 Aol/(1+Aolβ)
所以对于小的 Aolβ 值
就可以忽略 Aolβ
这样一来就只剩下 Aol/1
或者说就是 Aol
因此当 Aolβ 变小
闭环回路增益跟随 Aol 曲线
我们定义的电路的带宽为 1/β
和 Aol 曲线相交的频率
因此运算放大器数据表中
Aol 曲线可以近似到电路所需的闭环回路增益带宽
然而请注意 X 轴是对数的
因此以图形方式选定的带宽可能不够精确
另一种方法来确定带宽
是使用运算放大器数据表中的增益带宽积产品规格
增益带宽积是线性增益和带宽的乘积
因此在给定两个变数中的一个
可以得到另外一个解
例如让我们计算 OPA827 在 100V/V 的带宽吧
从数据表我们可以得知
增益带宽积为 22MHz
为求解带宽 从增益带宽公式告诉我们
带宽为增益带宽积除以线性增益
将 OPA827 增益带宽积 22MHz/100V/V 的增益
可以得到 220kHz 带宽
此计算可由观察数据表中 OPA827
开环回路增益来验证
如果画一条水平线在 100V/V
或 40dB 的闭环回路增益
直到它相交 Aol 我们找到了相应的带宽
大约为 200kHz
可以注意到 通过计算我们发现
带宽为 220kHz
它解决了图解可能错误地解释带宽为 200kHz
请注意计算出的带宽
须当 Aol 局限于
-20dB/dec 的速率下降才是有效的
虽然大部分的运算放大器都符合
但也有些特定的增益带宽积是有限的范围
此外考虑到数据表有增益带宽积
和 Aol 曲线的典型值
通常可以预期该值在室温下的变异数高达± 30%
在规定的温度范围外
可能有附加正负 30% 误差的变化
因此当考虑到放大器的带宽时
建议设计时保留您的设计裕度
现在让我们与 TINA-TI 仿真做比较
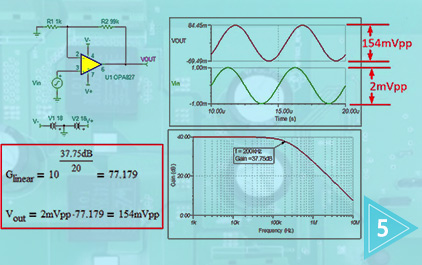
这里我们将一个 OPA140 设计为同相放大器组态
100V/V 或是 40dB 的闭环回路增益
该 OPA140 具有 11MHz 的增益带宽积
代入我们的闭环回路增益 100V/V
可以求出带宽为110kHz
在这里我们仿真的电路的闭环回路带宽
在 -3dB 点或 37dB 仿真带宽为 118kHz
虽然不完全一样
但我们计算和仿真结果是正相关的
最后让我们来看一下
一系列 TI 运算放大器的增益带宽
和其相对应的静态电流 Iq
此页我们列出增益带宽范围
从 12kHz 到 600MHz 放大器
OPA369 是一个非常低带宽的放大器
该电路是特别设计为非常低的静态电流
仅有 0.8uA 称为微功率电路
1MHz 为普遍放大器的带宽范围
如 OPA277
而 OPA350 和 OPA211 则具有更宽的带宽
以方便驱动 A/D 转换器
和其他高带宽应用
对非常高速应用中
可使用如 OPA835 和 OPA847
在一般情况下较宽的带宽运算放大器
需要较多的静态电流
不过有例外如 OPA835
那么为什么带宽和静态电流有关联
让我们来看看双极性和 CMOS 晶体管的物理关系
请注意 这里不是要深入理解晶体管理论
来了解放大器的带宽
这里的关键是
表示放大器带宽和静态电流间的物理原理
观察双极晶体管和 MOSFET 的 Transductions
转导或电流增益
可以看出 collector 基极和 drain 漏极
电流的直接关系
转导取倒数可得阻抗或 rgm
rgm 是运算放大器内部第一级的动态输出阻抗
此输出阻抗驱动米勒电容 Cc
rgm 和 Cc 的串联组合形成一个低通滤波器
该低通滤波器的主极点产生放大器内部的带宽
事实上你可以看到第三个方程式
是 RC 带宽公式
BW=2πRC 在最后的方程式
我们代入原有的 gm 公式来说明 gm 带宽的关联
其显示增加电流消耗
直接增加双极性运算放大器的带宽
但是如果是 MOSFET
带宽将依漏极电流平方根的比例增加
所以相较于双极晶体管
MOSFET 需要增加更大的电流来增加带宽
总结 这个视频讨论开环回路和闭环回路增益
增益带宽积 静态电流与带宽
我们还仿真电路的带宽
并显示带宽与我们计算结果的关联性
感谢您的时间
请尝试测验来检视对这个视频内容的理解吧
大家好 欢迎来到 TI Precision Labs 德州仪器高精度实验室 本次视频将介绍 运算放大器的 Bandwidth 带宽的第二部分 我们将探讨 open loop gain 开环回路增益 closed loop gain 闭环回路增益 gain bandwidth product 增益带宽积 Quiescent Current 静态电流与带宽的关系 也将仿真电路的带宽 并验证我们的计算结果 运算放大器的开环回路增益 或 Aol 代表由运算放大器 施加到输入端电压差的增益 运算放大器的 Aol 是无限大 然而真实世界的运算放大器 有超过 100 万 V/V 或 120dB 的开环回路增益 为了使一个放大器稳定 Negative feedback 负回授是必要的 可以经由 Rf 和 R1 来实现 有时被称为闭合回路 Rf 和 R1 代表 β 的网络 或回授系数 β 是经由测量 Vout 回授到运算放大器的 反相输入端变化来求得 在这个电路中我们看到 Rf 和 R1 产生一个电压分压器 因此 β=R1/(R1+Rf) 除运算放大器的开环回路增益 我们有所谓的闭环回路增益或 Acl 该方程 Acl=Aol/(1+Aolβ) 其中的 Aolβ 被称为回路增益 如图所示 这个方程式可以重新整理 闭环回路这一方程式可以简化 是由于有非常大的回路增益或 Aolβ 纵观回路增益公式可以看出 当 Aolβ 增加到无限大 你可以忽略分母中的 1 公式可简化为 Aol/Aolβ 将分子分母的 Aol 相消可得到 1/β 代入 β 可以得到 1+Rf/R1 的 闭环回路增益 这是一个常见的 none inverting 同相放大器闭环回路增益公式 重点是这个公式 只适用于开环回路增益非常高时 稍后我们将看到 当开环回路增益低会发生什么事情 然而在现实世界中 运算放大器的开环回路增益 具有低频的 dominant pole 主极点 如图所示 可以被看做是一个 RC filter滤波器 此仿真描绘了真实世界 运算放大器开环回路增益 在直流或低频 Aol 是非常大的 在这种情况下 它是 120dB 或 100万V/V 随着频率的增加 Aol 以 -20dB/dec 的速率降低 我们看到在 10MHz 时 开环回路增益为 0dB 或 1V/V 现在我们明白开环回路增益 会随着频率降低 此现象如何影响我们的闭环回路增益呢 回想一下 Aolβ 被称为回路增益 如果我们绘制了开环回路增益和 1/β 在对数轴 回路增益为两条曲线之间的差值 数学证明回路增益是 Aol 减掉 1/β 如底下的方程式所示 在这个例子中 1/β 为水平虚线在 20dB 注意 闭环回路增益在低频时为 1/β 在高频时为 Aol 曲线 还要注意在这 1/β 曲线和 Aol 曲线交错的点 是闭环回路带宽 让我们更深入地看看为什么闭环回路增益 在低频时为 1/β 而在高频时为 Aol 在低频时回路增益或 Aolβ 很大 请注意闭环回路增益为 Aol/(1+Aolβ) 所以对于较大 Aolβ 可以忽略 1 这一项 公式可简化为 Aol/Aolβ 将分子分母的 Aol 相消可得 1/β 在这种情况下 1/β 是一个熟悉的同相放大器增益方程式 1/β 是一个熟悉的同相放大器增益方程式 值为1+Rf/R1 在高频时 Aolβ 很小 请注意 闭环回路增益为 Aol/(1+Aolβ) 所以对于小的 Aolβ 值 就可以忽略 Aolβ 这样一来就只剩下 Aol/1 或者说就是 Aol 因此当 Aolβ 变小 闭环回路增益跟随 Aol 曲线 我们定义的电路的带宽为 1/β 和 Aol 曲线相交的频率 因此运算放大器数据表中 Aol 曲线可以近似到电路所需的闭环回路增益带宽 然而请注意 X 轴是对数的 因此以图形方式选定的带宽可能不够精确 另一种方法来确定带宽 是使用运算放大器数据表中的增益带宽积产品规格 增益带宽积是线性增益和带宽的乘积 因此在给定两个变数中的一个 可以得到另外一个解 例如让我们计算 OPA827 在 100V/V 的带宽吧 从数据表我们可以得知 增益带宽积为 22MHz 为求解带宽 从增益带宽公式告诉我们 带宽为增益带宽积除以线性增益 将 OPA827 增益带宽积 22MHz/100V/V 的增益 可以得到 220kHz 带宽 此计算可由观察数据表中 OPA827 开环回路增益来验证 如果画一条水平线在 100V/V 或 40dB 的闭环回路增益 直到它相交 Aol 我们找到了相应的带宽 大约为 200kHz 可以注意到 通过计算我们发现 带宽为 220kHz 它解决了图解可能错误地解释带宽为 200kHz 请注意计算出的带宽 须当 Aol 局限于 -20dB/dec 的速率下降才是有效的 虽然大部分的运算放大器都符合 但也有些特定的增益带宽积是有限的范围 此外考虑到数据表有增益带宽积 和 Aol 曲线的典型值 通常可以预期该值在室温下的变异数高达± 30% 在规定的温度范围外 可能有附加正负 30% 误差的变化 因此当考虑到放大器的带宽时 建议设计时保留您的设计裕度 现在让我们与 TINA-TI 仿真做比较 这里我们将一个 OPA140 设计为同相放大器组态 100V/V 或是 40dB 的闭环回路增益 该 OPA140 具有 11MHz 的增益带宽积 代入我们的闭环回路增益 100V/V 可以求出带宽为110kHz 在这里我们仿真的电路的闭环回路带宽 在 -3dB 点或 37dB 仿真带宽为 118kHz 虽然不完全一样 但我们计算和仿真结果是正相关的 最后让我们来看一下 一系列 TI 运算放大器的增益带宽 和其相对应的静态电流 Iq 此页我们列出增益带宽范围 从 12kHz 到 600MHz 放大器 OPA369 是一个非常低带宽的放大器 该电路是特别设计为非常低的静态电流 仅有 0.8uA 称为微功率电路 1MHz 为普遍放大器的带宽范围 如 OPA277 而 OPA350 和 OPA211 则具有更宽的带宽 以方便驱动 A/D 转换器 和其他高带宽应用 对非常高速应用中 可使用如 OPA835 和 OPA847 在一般情况下较宽的带宽运算放大器 需要较多的静态电流 不过有例外如 OPA835 那么为什么带宽和静态电流有关联 让我们来看看双极性和 CMOS 晶体管的物理关系 请注意 这里不是要深入理解晶体管理论 来了解放大器的带宽 这里的关键是 表示放大器带宽和静态电流间的物理原理 观察双极晶体管和 MOSFET 的 Transductions 转导或电流增益 可以看出 collector 基极和 drain 漏极 电流的直接关系 转导取倒数可得阻抗或 rgm rgm 是运算放大器内部第一级的动态输出阻抗 此输出阻抗驱动米勒电容 Cc rgm 和 Cc 的串联组合形成一个低通滤波器 该低通滤波器的主极点产生放大器内部的带宽 事实上你可以看到第三个方程式 是 RC 带宽公式 BW=2πRC 在最后的方程式 我们代入原有的 gm 公式来说明 gm 带宽的关联 其显示增加电流消耗 直接增加双极性运算放大器的带宽 但是如果是 MOSFET 带宽将依漏极电流平方根的比例增加 所以相较于双极晶体管 MOSFET 需要增加更大的电流来增加带宽 总结 这个视频讨论开环回路和闭环回路增益 增益带宽积 静态电流与带宽 我们还仿真电路的带宽 并显示带宽与我们计算结果的关联性 感谢您的时间 请尝试测验来检视对这个视频内容的理解吧
大家好
欢迎来到 TI Precision Labs
德州仪器高精度实验室
本次视频将介绍
运算放大器的 Bandwidth 带宽的第二部分
我们将探讨 open loop gain
开环回路增益
closed loop gain 闭环回路增益
gain bandwidth product 增益带宽积
Quiescent Current 静态电流与带宽的关系
也将仿真电路的带宽
并验证我们的计算结果
运算放大器的开环回路增益
或 Aol 代表由运算放大器
施加到输入端电压差的增益
运算放大器的 Aol 是无限大
然而真实世界的运算放大器
有超过 100 万 V/V
或 120dB 的开环回路增益
为了使一个放大器稳定
Negative feedback 负回授是必要的
可以经由 Rf 和 R1 来实现
有时被称为闭合回路
Rf 和 R1 代表 β 的网络 或回授系数
β 是经由测量 Vout 回授到运算放大器的
反相输入端变化来求得
在这个电路中我们看到 Rf 和 R1
产生一个电压分压器
因此 β=R1/(R1+Rf)
除运算放大器的开环回路增益
我们有所谓的闭环回路增益或 Acl
该方程 Acl=Aol/(1+Aolβ)
其中的 Aolβ 被称为回路增益
如图所示 这个方程式可以重新整理
闭环回路这一方程式可以简化
是由于有非常大的回路增益或 Aolβ
纵观回路增益公式可以看出
当 Aolβ 增加到无限大
你可以忽略分母中的 1
公式可简化为 Aol/Aolβ
将分子分母的 Aol 相消可得到 1/β
代入 β 可以得到 1+Rf/R1 的
闭环回路增益
这是一个常见的 none inverting
同相放大器闭环回路增益公式
重点是这个公式
只适用于开环回路增益非常高时
稍后我们将看到
当开环回路增益低会发生什么事情
然而在现实世界中
运算放大器的开环回路增益
具有低频的 dominant pole 主极点
如图所示 可以被看做是一个 RC filter滤波器
此仿真描绘了真实世界
运算放大器开环回路增益
在直流或低频 Aol 是非常大的
在这种情况下
它是 120dB 或 100万V/V
随着频率的增加 Aol 以 -20dB/dec 的速率降低
我们看到在 10MHz 时
开环回路增益为 0dB 或 1V/V
现在我们明白开环回路增益
会随着频率降低
此现象如何影响我们的闭环回路增益呢
回想一下 Aolβ 被称为回路增益
如果我们绘制了开环回路增益和 1/β 在对数轴
回路增益为两条曲线之间的差值
数学证明回路增益是 Aol 减掉 1/β
如底下的方程式所示
在这个例子中
1/β 为水平虚线在 20dB
注意 闭环回路增益在低频时为 1/β
在高频时为 Aol 曲线
还要注意在这 1/β 曲线和 Aol 曲线交错的点
是闭环回路带宽
让我们更深入地看看为什么闭环回路增益
在低频时为 1/β
而在高频时为 Aol
在低频时回路增益或 Aolβ 很大
请注意闭环回路增益为
Aol/(1+Aolβ)
所以对于较大 Aolβ
可以忽略 1 这一项
公式可简化为 Aol/Aolβ
将分子分母的 Aol 相消可得 1/β
在这种情况下
1/β 是一个熟悉的同相放大器增益方程式
1/β 是一个熟悉的同相放大器增益方程式
值为1+Rf/R1
在高频时 Aolβ 很小
请注意 闭环回路增益为 Aol/(1+Aolβ)
所以对于小的 Aolβ 值
就可以忽略 Aolβ
这样一来就只剩下 Aol/1
或者说就是 Aol
因此当 Aolβ 变小
闭环回路增益跟随 Aol 曲线
我们定义的电路的带宽为 1/β
和 Aol 曲线相交的频率
因此运算放大器数据表中
Aol 曲线可以近似到电路所需的闭环回路增益带宽
然而请注意 X 轴是对数的
因此以图形方式选定的带宽可能不够精确
另一种方法来确定带宽
是使用运算放大器数据表中的增益带宽积产品规格
增益带宽积是线性增益和带宽的乘积
因此在给定两个变数中的一个
可以得到另外一个解
例如让我们计算 OPA827 在 100V/V 的带宽吧
从数据表我们可以得知
增益带宽积为 22MHz
为求解带宽 从增益带宽公式告诉我们
带宽为增益带宽积除以线性增益
将 OPA827 增益带宽积 22MHz/100V/V 的增益
可以得到 220kHz 带宽
此计算可由观察数据表中 OPA827
开环回路增益来验证
如果画一条水平线在 100V/V
或 40dB 的闭环回路增益
直到它相交 Aol 我们找到了相应的带宽
大约为 200kHz
可以注意到 通过计算我们发现
带宽为 220kHz
它解决了图解可能错误地解释带宽为 200kHz
请注意计算出的带宽
须当 Aol 局限于
-20dB/dec 的速率下降才是有效的
虽然大部分的运算放大器都符合
但也有些特定的增益带宽积是有限的范围
此外考虑到数据表有增益带宽积
和 Aol 曲线的典型值
通常可以预期该值在室温下的变异数高达± 30%
在规定的温度范围外
可能有附加正负 30% 误差的变化
因此当考虑到放大器的带宽时
建议设计时保留您的设计裕度
现在让我们与 TINA-TI 仿真做比较
这里我们将一个 OPA140 设计为同相放大器组态
100V/V 或是 40dB 的闭环回路增益
该 OPA140 具有 11MHz 的增益带宽积
代入我们的闭环回路增益 100V/V
可以求出带宽为110kHz
在这里我们仿真的电路的闭环回路带宽
在 -3dB 点或 37dB 仿真带宽为 118kHz
虽然不完全一样
但我们计算和仿真结果是正相关的
最后让我们来看一下
一系列 TI 运算放大器的增益带宽
和其相对应的静态电流 Iq
此页我们列出增益带宽范围
从 12kHz 到 600MHz 放大器
OPA369 是一个非常低带宽的放大器
该电路是特别设计为非常低的静态电流
仅有 0.8uA 称为微功率电路
1MHz 为普遍放大器的带宽范围
如 OPA277
而 OPA350 和 OPA211 则具有更宽的带宽
以方便驱动 A/D 转换器
和其他高带宽应用
对非常高速应用中
可使用如 OPA835 和 OPA847
在一般情况下较宽的带宽运算放大器
需要较多的静态电流
不过有例外如 OPA835
那么为什么带宽和静态电流有关联
让我们来看看双极性和 CMOS 晶体管的物理关系
请注意 这里不是要深入理解晶体管理论
来了解放大器的带宽
这里的关键是
表示放大器带宽和静态电流间的物理原理
观察双极晶体管和 MOSFET 的 Transductions
转导或电流增益
可以看出 collector 基极和 drain 漏极
电流的直接关系
转导取倒数可得阻抗或 rgm
rgm 是运算放大器内部第一级的动态输出阻抗
此输出阻抗驱动米勒电容 Cc
rgm 和 Cc 的串联组合形成一个低通滤波器
该低通滤波器的主极点产生放大器内部的带宽
事实上你可以看到第三个方程式
是 RC 带宽公式
BW=2πRC 在最后的方程式
我们代入原有的 gm 公式来说明 gm 带宽的关联
其显示增加电流消耗
直接增加双极性运算放大器的带宽
但是如果是 MOSFET
带宽将依漏极电流平方根的比例增加
所以相较于双极晶体管
MOSFET 需要增加更大的电流来增加带宽
总结 这个视频讨论开环回路和闭环回路增益
增益带宽积 静态电流与带宽
我们还仿真电路的带宽
并显示带宽与我们计算结果的关联性
感谢您的时间
请尝试测验来检视对这个视频内容的理解吧
手机看
扫码用手机观看
 视频简介
视频简介
5.2 TI 高精度实验室 - 带宽 2
所属课程:TI 高精度实验室放大器系列 - 带宽
发布时间:2018.05.21
视频集数:5
本节视频时长:00:12:14
您是否知道在计算运算放大器带宽时应始终使用非反相增益?你知道为什么带宽会影响Iq吗?
除了回答这些问题外,我们还会向您展示几乎所有您想了解的关于运放带宽的信息,包括:
了解如何在波特图上使用Aol,环路增益和1 / beta来预测放大器在整个频率上的性能。
使用电阻器,电容器和放大器频率限制来推导极点和零点位置的方程。
在波特图上标绘极点和零点的实践技巧,并涵盖闭环带宽的图形和数学计算。
使用波特图和范围结果研究时域与频域的关系。
通过使用放大器内部电路的简化模型了解带宽和Iq之间的关系。
本系列视频涵盖运算放大器带宽理论,然后将其应用于包括TINA-TI电路仿真和使用带测试设备的实际电路的实验的动手实验室。
 未学习 5.1 TI 高精度实验室 - 带宽 1
未学习 5.1 TI 高精度实验室 - 带宽 1
 未学习 5.2 TI 高精度实验室 - 带宽 2
未学习 5.2 TI 高精度实验室 - 带宽 2
 未学习 5.3 TI 高精度实验室 - 带宽 3
未学习 5.3 TI 高精度实验室 - 带宽 3
 未学习 5.4 TI 高精度实验室 - 带宽 4
未学习 5.4 TI 高精度实验室 - 带宽 4
 未学习 5.5 TI 高精度实验室 - 带宽 实验
未学习 5.5 TI 高精度实验室 - 带宽 实验